基于ADC 和改进云模型的数据链对抗侦察效能评估

龚 燕，刘雅奇，朱然刚

（国防科技大学电子对抗学院，合肥 230037）

0 引言

数据链作为电子战中的通信铰链，稳定快速大量地传递战场信息和态势，无愧于战争力量的“倍增器”。近年来，外军数据链技术更是突飞猛进，向着更为通用稳定抗干扰的趋势高速发展着。因此，在研究数据链技术本身的同时，对数据链系统的电子对抗行动同样不可忽视。本文采用结合Delphi法、层次分析法和分析经过改进的ADC 模型［1］的基础上，构建数据链对抗侦察效能评估体系，在得到定量的侦察效能指标值后，采用经Vague 集相似性度量法改进后的云理论，对指标值进行定性的转换，以实现直观的行动效果评价，使得评估体系更为完善实用。

1 数据链对抗侦察指标

电子对抗侦察主要分为信号的发现截获、分析识别、参数估计和测向定位［2］，因此，把这4 个指标作为数据链侦察的一级指标。

数据链信号的检测截获概率是指敌方数据链系统利用伪随机的跳频图案控制信号载波，在短时间内完成多个频率的跳变，达到抗侦察抗干扰的效果，而我方利用宽带接收机等设备，在时频空域条件皆满足的情况下，对信号完成侦收工作的概率［3］。

分析识别是指在非合作通信条件下，分析设备在接收设备滤波输出后，对信号的调制方式等进行分析与识别，其中还包括对信号调制参数的估计［4］，参数估计的准确性对下一步测向定位有较大的影响作用。

测向定位概率是指测向设备对接收到的信号进行ADC 等处理，提取信号中的方位信息，给出区间范围，而这个范围的准确程度则是作为指标评估测向的效能。

数据链侦察的效能指标体系构建如图1 所示。

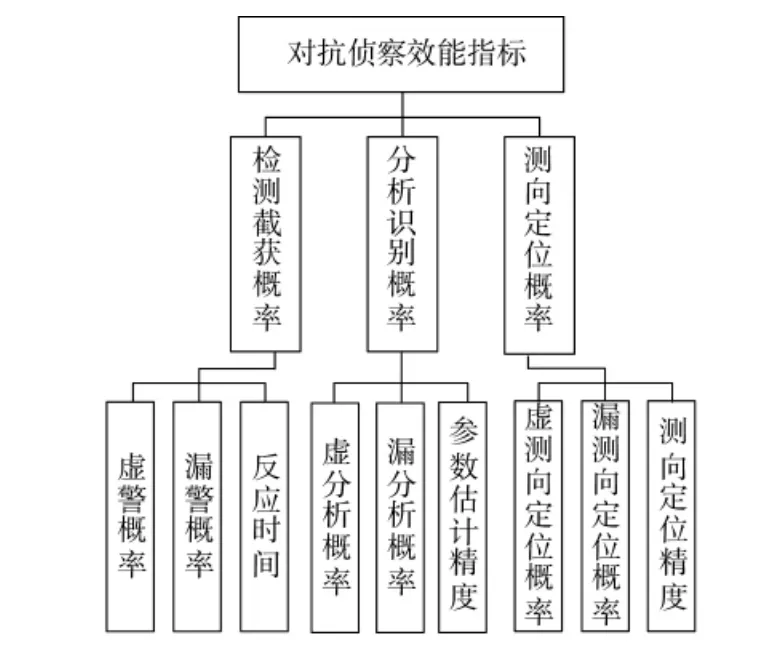
图1 数据链对抗侦察效能指标体系

2 ADC 模型

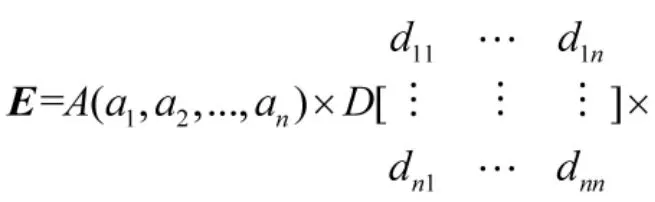
首先，由于数据链信号的持续时间短、战场态势瞬息万变，本文认为数据链对抗系统的故障修复在短时间内无法完成，因此，某型数据链对抗系统在工作时只有两种状态，正常工作或故障，ai表示数据链对抗系统处于某一工作状态时的概率，因此，可信度矩阵A=（a1，a2），ai的计算公式如下

式中，MTBF 为数据链对抗系统维持正常工作的平均时间，MTTR 为由故障至正常工作平均所需时间，则a1为系统正常工作概率，a2为系统故障概率。根据某型数据链对抗设备参数，MTBF=500 h，MTTR=0.8 h，计算得：A=（0.998 4，1.597 4）。

可信度矩阵D 中元素dij表示数据链对抗系统从i 状态切换至j 状态的概率，上文提到默认故障修复时间过长，因此，在战斗中系统不可能从故障切换为正常工作状态，而且一般认为系统的正常工作时间服从指数分布，本文假设某次战斗的时间长度为4 h，得到矩阵D 为

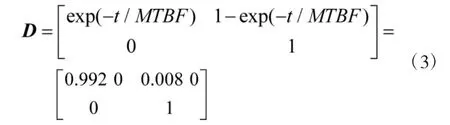
能力矩阵C 的构建步骤：

1）利用Delphi 法得到专家意见并转化为判断矩阵

将指标两两分组，交由专家评分决定相对重要程度，评分规则根据层次分析法将定性的指标重要程度划为9 个级别，若A 指标重要程度默认为1，组内B 指标相对重要一些，可打分为2 或3 或4，重要许多则打分5 或6 或7，相对A 极其重要则为8 或9，反之则为1/2、1/3 等［1］，以此类推，具体可由专家结合指标实际依次比较打分。

2）求出矩阵特征向量，得到指标权重

根据公式

求解所得矩阵W 中元素wi即为判断矩阵Q 的特征向量也是各项指标对应权重。

利用行和归一法，得到wi为

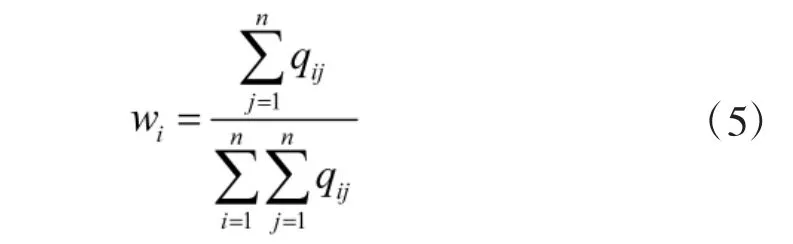
3）检验权重的合理性，首先检验矩阵Q 的协调性和随机性。

根据一致性比列值θCR与0.1 的大小比较，判断是否合理。若θCR＜0.1，则权重有效。

计算公式如下

式中，θRI为一致性指标，文献［6］中提供了指标数值表，本文截取部分于表1 中，如下所示：

表1 一致性指标值查询表

4）一致性检验通过后，得到能力矩阵C

式中，ui表示各指标归一化后的值。

3 云模型

在实际作战条件下，语言文字信息相较于ADC模型直接产生的数据信息而言，是一种更利于决策的信息表达形式。为了进一步形象地反映能力矩阵对侦察效果的评估结果，以便于作战指挥人员根据战时情况有效制定作战计划，本文采用基于Vague集改进的云理论对数据指标进行定性的转换。

3.1 云模型构建方法

云理论是李德毅院士提出的在定性的概念与定量的数值之间的映射［7-8］，云模型为论域U 中元素x 指向定性的概念部分T 的映射，用数学公式可描述为

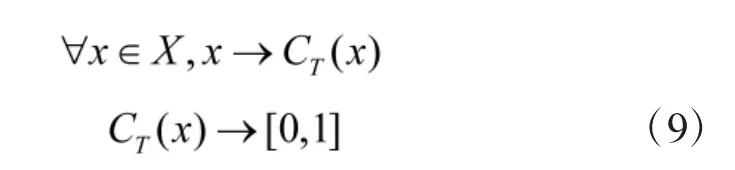
式中，C（Tx）表示元素对定性概念的隶属度。云模型具有一定的模糊性与不确定性，每个云模型由多个云滴（云滴即为元素x）共同组成，该模型一般用3个特征值唯一确定，分别为期望值Ex、熵En、超熵He，其中，期望值Ex代表着云重心的位置，云重心为重心的高度和位置的乘积，熵En表示云代表的定性概念的模糊程度，超熵He则代表了其不确定的程度，因此，熵En、超熵He的值越小，则云越聚拢，反之则云对应的隶属度分布越离散。

云模型定量值至定性概念的转换一般分为4 步：

1）定性的自然语言描述与定量区间映射关系的确立

与获得权重系数的方法不同，此时的映射关系不再采用专家打分法，而是采用黄金分割法［9］进行对应的转换，该方法的主要原则为相邻云模型的特征值遵守黄金分割原则，即

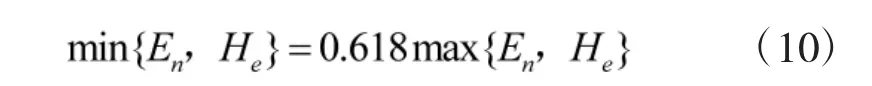
基于前文将指标归一化（ui∈［0，1］）的基础上，本文将定性描述划为5 个标度，如表2 所示。

表2 指标评价定性标度表

2）单个指标的云特征值计算

云重心位置的计算

熵计算

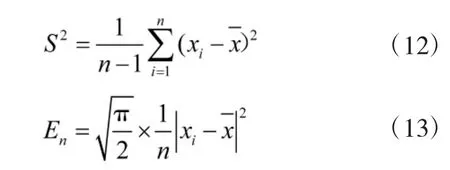
超熵计算

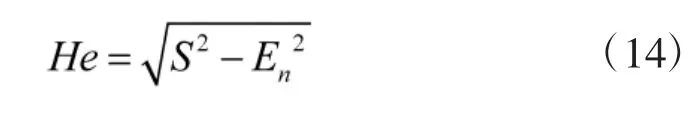
3）将各个云模型的值代入以下进行综合云的特征值计算

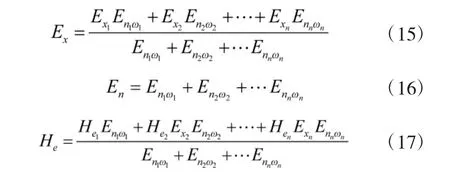
4）加权偏离度的计算

5）采用云测评器将所得相似度度量转化为定性评价，云测评器的产生原理如图3 所示。

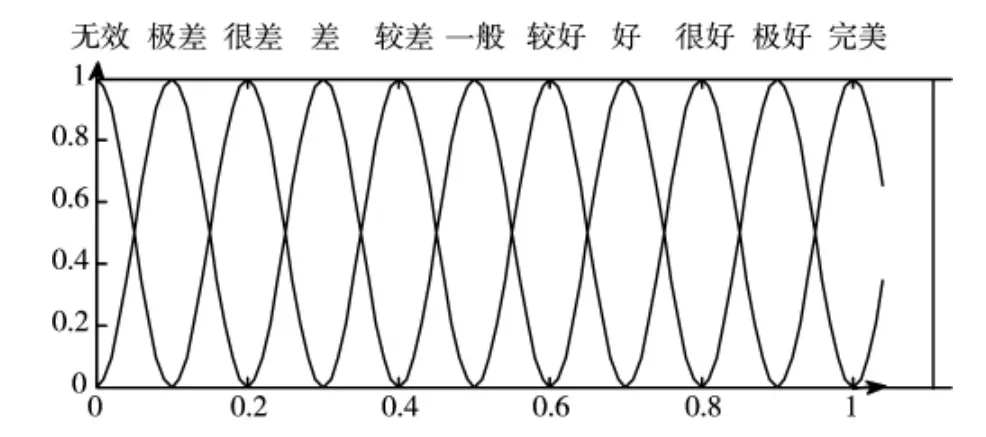
图3 云测评器原理

3.2 基于Vague 集的改进云模型

由于仅仅用两种状态的云重心差值不能全面地反映出实际效果与理想效果的差距，因此，在综合云与标准云的相似性度量中，引入了基于“得票再分配”背景下提出的Vague 集相似性度量来进一步完善。Vague 集与云模型同样面向隶属度为［0，1］的对象，且具有相当的模糊处理能力，因此，合理构建映射关系，将使云模型的转换准确度进一步提升。云模型的改进分为两步：

1）确立Vague 集隶属度函数与云模型的特征值的对应关系

因此，在云模型中可将对应值分别列出为：

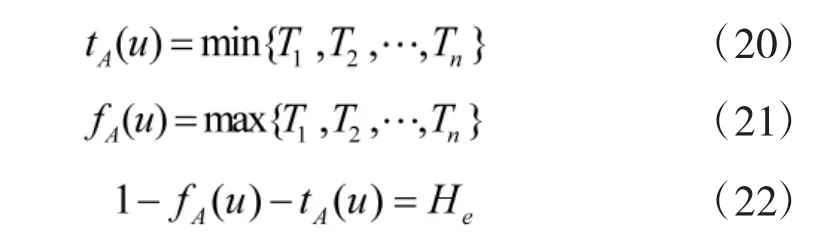
2）相似性度量方法的确定

Vague 集的相似性度量有两种方法，使用区别在于真假隶属度函数是否独立，考虑到云模型中超熵为熵的熵，且熵的计算与期望值也相关，因此，认为采用不独立函数对应的权重再分配法较为合适［11-12］。

其中

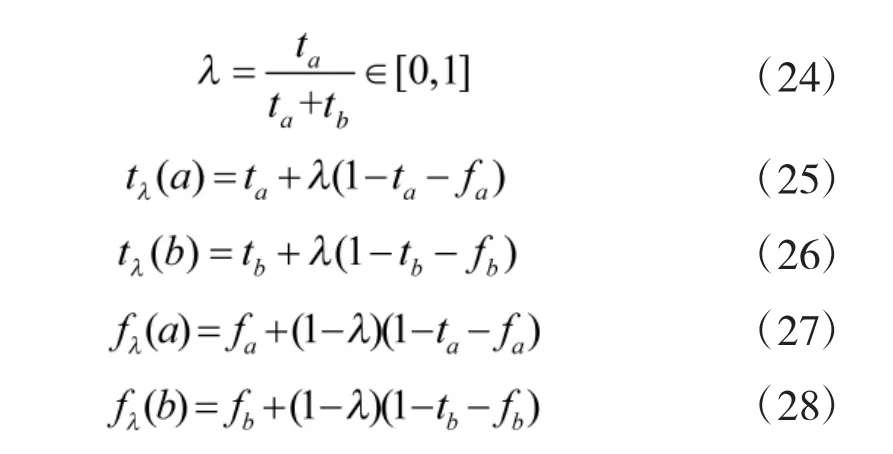
4 侦察指标实例计算与分析

统计专家打分结果并总结为矩阵Q，文中以侦察体系中9 个二级指标为例，得到的矩阵如下

结合判断矩阵Q，由式（4）、式（5）求解，得数据链对抗侦察指标体系中权重值如下页表3 所示。

又由式（6）、式（7）检验得θCR=0.064＜0.1 即权重可用。

以二级指标为例，根据演习、计算机仿真实验获得大量数据，求得二级指标每个指标对应的云模型特征值罗列如表4 所示。

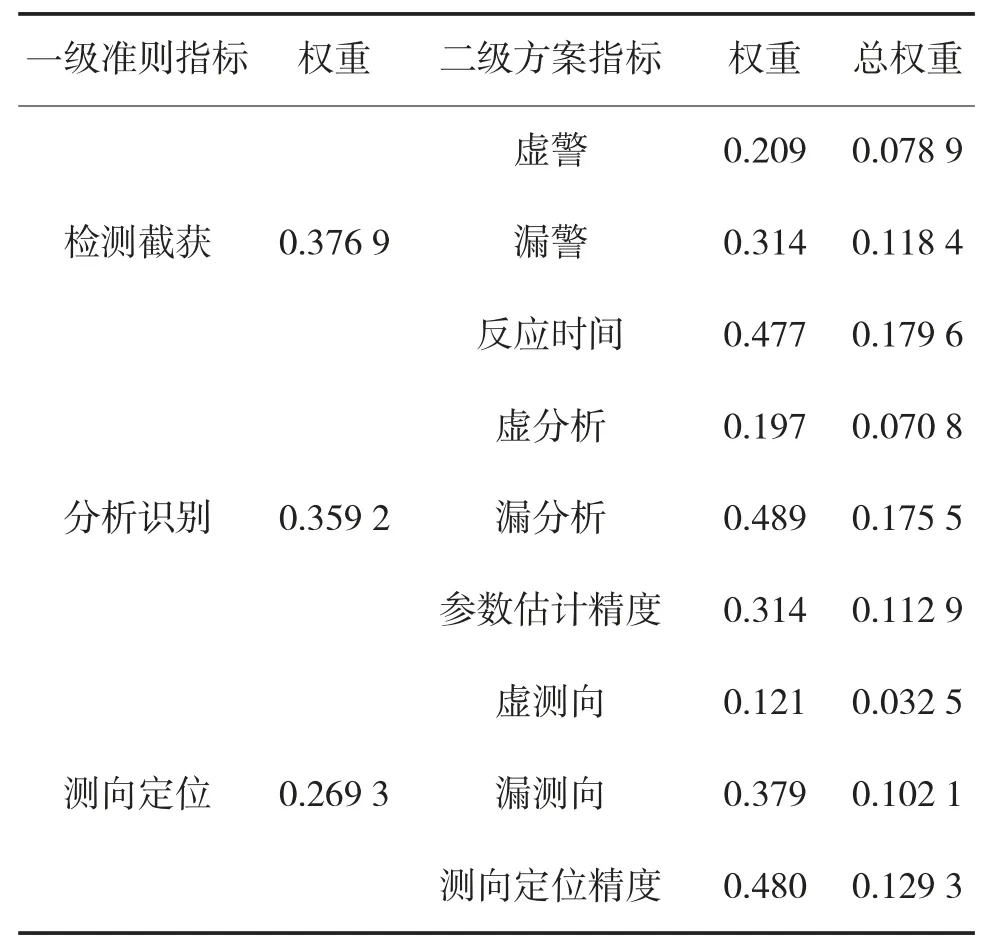
表3 数据链对抗侦察指标权重

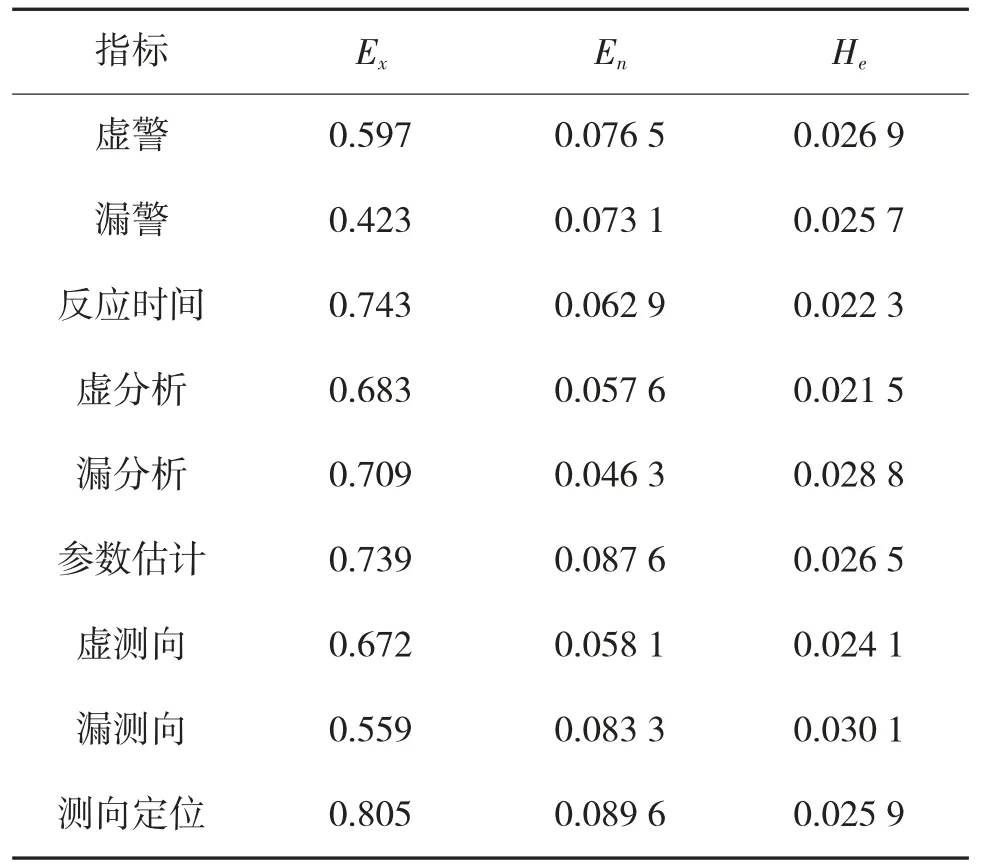
表4 各指标对应的云特征值

表5 相似度度量参数值

将数据导入云测评器可知，此次数据链对抗侦察行动效果为好。

而采用传统的加权偏离度θ 来衡量相似度时，可根据式（18）以及式（19）得到TiG=（0.414，0.526，0.043 6，0.016 5，0.054 2，0.0213，0.404，0.104，0.317），θ=0.18，相似度为1-θ=0.82，则对应结果为很好。由各项指标单独来看，此次数据链对抗侦察行动的效果算不上很好，由此可见，Vague 集的相似性度量较传统的加权偏离度而言要更为准确。

5 结论

基于ADC 等方法的基础上确定数据链对抗侦察评估指标的权重，弥补了云模型的不确定性和模糊性，在定量指标结果至定性评价的转换过程中，将加权偏离度法与经Vague 集相似性度量法改进后的云模型进行试验比较，得到更为准确的定性评估。本文确立并完善了数据链对抗侦察效能指标体系及评估方法，为下一步数据链对抗干扰效能的计算及评估打下基础。