基于MPSO 的地面防空群维修任务规划研究*
2019-09-17左文博赵英俊张迪哲
左文博,赵英俊,张迪哲,和 柳
(1.空军工程大学防空反导学院,西安 710051;2.解放军93942 部队,陕西 咸阳 712000)
0 引言
地面防空群是信息化条件下地面防空作战的主要编组样式,保卫某一重要区域内的目标安全,通常由群指控中心、不同种类、型号的多个防空火力单元混编构成。地面防空群的维修任务主要包括依托本级维修保障人员的现地换件维修和依托支援保障点的抢修力量实施战场抢修。现地的换件维修消耗时间小、难度小,便于实施。对于依托支援保障点的抢修由于其维修保障资源分散,维修时间长,是战时地面防空群的维修任务规划需重点考虑的问题,属于在一定约束条件下多任务和多资源的多目标优化问题。
多个文献关于维修任务规划问题开展了研究。文献[1-2]针对战时维修任务的动态调度问题,以最短维修保障时间为目标进行维修任务规划,建立数学模型,并考虑维修力量的维修能力和互相之间支援的情况。装备维修任务规划的前提是对维修任务优先级进行分类,文献[3]针对装备维修任务优先级分类开展了研究,构建了影响维修任务优先级的多个属性,提出一种基于犹豫模糊矩阵的权重确定方法,并通过算例进行了验证。文献[4-5]针对装备维修保障资源调度问题开展了研究,通过问题分析,抽象建立维修保障资源调度决策模型,采取不同的算法进行求解。文献[6]建立了基于遗传算法的维修任务规划策略,根据装备维修工序特点,建立了以总维修工时最短为目标的维修任务规划模型,采用遗传算法进行求解。文献[7]开展伴随修理中的维修任务调度策略研究,应用离散事件仿真方法建立了装备作战单元伴随修理的仿真模型,并进行评估,为维修任务调度策略提供了一种新的研究思路。这些研究对于装备维修任务规划问题具有一定借鉴,但部分研究存在不足,主要表现在:研究对象多为单个装备,建立的模型目标函数过于单一,约束条件较为简单,算法效率不高,没有体现出装备维修任务规划问题的复杂性和特殊性。本文根据地面防空群的维修任务规划特点,以维修任务的优先级、维修时间和维修保障资源消耗为目标,建立维修任务规划多目标优化模型,并采取改进的自适应粒子群优化算法进行求解,得到较为满意的结果。本文的研究思路和方法适用于地面防空群的维修任务规划问题,可以为部队维修保障决策提供理论支撑和方法借鉴。
1 地面防空群维修任务规划建模
1.1 问题分析
地面防空群作为一个区域型混编的防空体系,是由分散部署于某一区域的多个类型、型号火力单元构成。考虑到战场环境的复杂性和特殊性,维修支援保障点通常独立部署于火力单元附近一定距离,支援维修保障力量依托设置的多个维修支援保障点,对地面防空群内的多个火力单元实施战场抢修。地面防空群虽然是由多个不同型号的地面防空装备组成,但各个火力单位都是由指控设备、制导装备、发射装备、导弹等装备构成,各个不同型号的装备可以按照装备类型划分为专用装备、同型装备和通用装备,在进行维修任务规划时,可以充分考虑其特点,采取“专装专保、同装统保、通装联保”的维修原则,实行联合一体化的维修保障模式。高强度的信息化战争使得装备维修任务繁重,针对地面防空群内多个维修任务需求的情况,为了实施精准高效的维修保障,应明确维修任务规划流程,制定科学合理的维修任务规划方案,确保科学、高效完成地面防空群维修保障任务,维修任务规划的具体流程如图1 所示。

图1 地面防空群维修任务规划流程
为了描述地面防空群维修任务规划问题,将地面防空群内的各个防空火力作战单元作为每个维修需求点,将分散部署于周边的抢修力量作为维修支援点。根据防空作战规律特点和地面防空群装备维修保障要求,地面防空群的维修任务规划问题在决策过程中应重点考虑以下因素:
1)维修任务的优先级。战时环境下,维修力量和维修保障等资源有限。当需要完成多个维修任务时,必须对维修任务的优先级进行排序。根据地面防空群内火力单元作战任务的重要性要求,应当首先保障重要的火力单元装备的战备完好性,即先对维修任务优先级高的火力单元实施支援抢修,维修任务完成后,再对较低级别维修任务的火力单元实施抢修。
2)维修时间最短。维修时间包含从维修支援保障点到达维修需求点和实施维修的时间。最短的维修时间能够确保作战单元快速恢复战斗力。由于各个火力单元和维修支援保障点均分散部署,从维修支援保障点到达维修需求点的时间长短不同,应进行合理规划确定总的最短的维修时间。
3)维修保障资源消耗最少。战时空防对抗激烈,战斗强度大,地面防空群维修保障资源需求巨大,由于战场环境的复杂性和特殊性,维修保障资源是有限的。维修保障资源消耗从维修支援点数目和支援抢修资源损耗两方面进行考虑。一方面需要的维修支援点数目越少,表明维修保障过程所需的人力物力资源越少,便于作战区域内统一指挥调度;另一方面支援抢修过程中消耗的资源越少,越有利于将结余的资源进行其他维修保障。
1.2 多目标优化函数的构建
基于上述分析,地面防空群的维修任务规划将各个火力单元抽象为维修需求点,各个维修抢修机构抽象为维修支援保障点,以维修任务的优先级、维修时间最短和维修保障资源消耗最少为目标,建立如下的地面防空群的维修任务规划模型:

式中,i(i=1,2,…,m)表示维修支援点,j(j=1,2,…,n)表示维修任务需求点;xjk为维修任务调度标识符,若在维修任务完成能力范围内,则xjk=0,否则xjk=1;pi为维修任务优先级权值,取值范围为0~1;Cij为从维修支援点i 向维修需求点j 实施维修的判断矩阵;tij为从维修支援点i 向维修需求点j 进行维修所需的时间;dij为从维修支援点i 向维修需求点j进行维修的保障资源的损耗量;式(1)表示未完成任务的优先级尽可能小,即完成的高优先级任务尽可能多;式(2)表示维修时间最短;式(3)表示维修保障资源损耗最少。
1.3 约束条件分析
维修任务规划的约束主要考虑维修任务和资源供需关系、维修时间限制和维修资源消耗要求等因素,约束条件具体描述为:

2 模型求解
2.1 基于置信度法的多目标函数处理
上述建立的维修任务规划模型为组合优化问题,模型具有多个目标函数和多个约束条件,属于典型的NP-hard 问题[8]。为此,将多目标函数通过处理转化为单目标函数进行求解。具体处理步骤为:
1)目标参量的标准化处理。目标函数中的维修任务优先级、维修时间和维修保障资源消耗是不同量纲的目标参数,首先进行目标参数的无量纲标准化处理。

2)目标参量的权重值确定。置信度法将专家对目标参量的重要性和战场环境变化导致判断的确定程度进行融合处理。考虑到防空作战环境瞬息万变,不同的作战强度和作战紧迫程度会对目标参量的权重产生一定影响。因此,采用将目标参量的重要性和战时环境的变化相结合的方法,可以避免确定的权重值与实际偏离较大,具有较好的实时性和客观性。具体步骤如下:邀请p 位防空作战维修保障方面的专家,对目标参量的权重依据重要性从1~9 进行打分,同时依据战场环境变化给出自己的判断水平,从0~1 给出置信度。若第j 位专家给出的重要性为xij,置信度为ωij,则对目标参量fi可得到p个数对(xij,ωij),由此可计算出目标参量的权重为:
3)将多目标优化问题转换为单目标求解问题,具体表达式为:

式中,ωi为各个目标参量的权重值,fi为标准化处理后的目标参量,l 为目标参量个数,取值为3。
2.2 改进的自适应粒子群算法
对于多目标问题的求解,以往的算法多为启发式算法、完全搜索算法或多层规划算法,这些算法的求解效率不高,结果往往无法令人满意。粒子群算法(Particle Swarm Optimization,PSO)是一类全局随机进化算法,可以对整个参数空间进行高效并行搜索,收敛速度快,但存在精度较低、易发散等缺点[9-11]。为此,可以通过采用多个子种群、改进微粒学习对象选取策略,以及与其他算法混合等方法来提高PSO 算法的性能。本文提出的改进的自适应粒子群算法(Modified PSO,MPSO)通过改进算法中惯性权重这个重要的参数,动态地平衡算法在每一代的探索与开发能力,自适应参数的具体策略是:将粒子按照其最优位置性能从优到劣进行排序,排在第i 位粒子的惯性权重及对应的加速系数为:

式中,wmax,wmin分别为设定的最大、最小惯性权值;Np为种群规模;粒子i 的加速系数cij,ci2根据惯性权重wi进行自适应调整。
另外,通过适当共享优秀邻域个体的信息可以提高不同粒子平衡点的多样性,以此提高搜索效率。将pg替换为按个体最优位置排序后最好的S 个体最优位置的加权平均pag,而将pi替换为排序后pi-1与pi的加权平均paj:

式中,fk=f(pk),为pk对应的适应度。
则改进的自适应粒子群算法的粒子速度更新表达式为:

粒子位置表达为:

综上分析,改进的自适应粒子群算法的具体求解步骤为:
Step1:随机初始化各个粒子的位置与速度,将每个粒子的当前位置设置为Xpbest,j,粒子群中最佳粒子的当前位置设置为Xgbest;
Step2:计算各个粒子的适应度;
Step3:将每个粒子的个体最优秀位置pi、全体最优位置pg和对应的适应度进行更新,并按其个体最优位置性能从优到劣进行排序;
Step4:根据式(8)和式(9)计算每个粒子的惯性权重wi和加速系数ci1、ci2,并根据式(10)和式(11)计算pai和pag;
Step5:更新每个粒子的位置和速度,判断是否满足终止条件(达到最大迭代次数),若满足则循环结束,否则跳转至Step2 继续循环。
3 算例验证
以某地面防空群为例验证算法的有效性,假设该群包含多个型号的防空火力单元,维修任务需求点为30 个,总的装备维修保障支援点为10 个,某时刻地面防空群维修保障支援点的供应态势矩阵如A 所示,矩阵A 表示维修保障支援点i 能够提供p 种维修保障资源的数量,例如a13=9 表示在第3 个维修保障支援点中,能够提供第1 种维修保障资源的数量为9。另外,最大维修保障时间T≤0.5 h,单次维修保障最大资源消耗ei≤0.4。按照基于置信度的多目标函数处理得到各目标参数的权重ω(f1)=0.482,ω(f2)=0.365,ω(f3)=0.153。

分别采用改进的自适应粒子群与传统粒子群算法进行仿真对比,算法的参数设置为:惯性权重wmax=0.9,wmin=0.4,加速度常数c1=c2=1.8,粒子数目n=20,最大迭代次数itermax=300。运用MATLAB 软件仿真,得到两种算法的进化收敛过程图如图2所示。

图2 算法进化收敛示意图
从图中可以看出,改进的自适应粒子群优化算法的收敛速度更快,且算法求解结果的质量优于传统粒子群算法。同时,考虑到区域联合防空作战要求及战场环境的复杂性,分别以10 个、30 个和50个维修任务需求点为背景,分别进行100 次仿真模拟,将两种算法的结果取均值进行比较,具体结果如表1 所示。
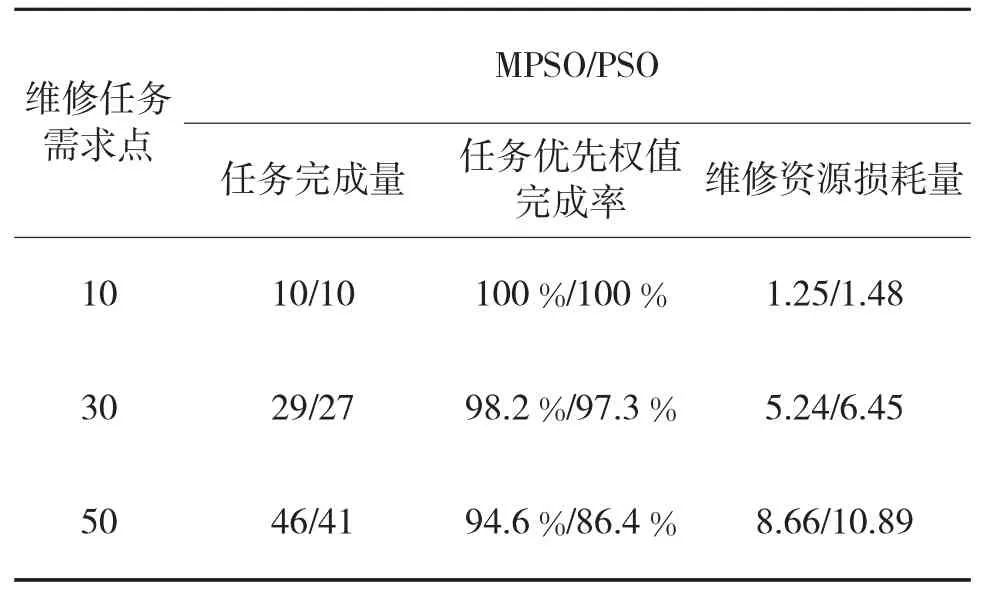
表1 多个维修任务需求点下两种算法的结果对比
可以看出,3 种不同数量的维修任务需求点条件下,改进的自适应粒子群优化算法的结果优于传统粒子群算法,维修任务完成量和任务优先权值完成率提高,维修资源损耗量降低。同时,维修任务需求点的数量越多,改进的自适应粒子群优化算法在任务完成量、权值完成率、资源损耗等指标结果上越优于传统粒子群算法。
图3 为维修任务需求点为30 个时,以维修任务规划优先权值完成百分比为目标,采用两种算法的对比结果。可以看出,改进的自适应粒子群算法的任务优先权值完成率一直保持在98%以上,能够很好地满足战时地面防空群维修任务规划的需求。

图3 任务规划权值完成率分析
4 结论
本文根据地面防空作战维修保障特点,建立了维修任务规划流程,以维修任务的优先级、维修时间和维修保障资源消耗为目标函数,构建了地面防空群维修任务规划模型,采用改进的自适应粒子群算法对模型进行了求解。算例结果表明,构建的多目标数学模型适合地面防空群的维修任务规划问题,新算法在收敛速度和求解质量方面均表现出良好的性能,维修任务规划权值完成率很高,能够较好地解决战时地面防空群的维修任务规划问题。后续研究进一步对维修任务模型进行描述,以及分析维修供需动态变化对于维修任务规划的影响。
