基于新型PSGA算法的通航物流配载效能优化问题研究

张昊

摘要：2012年国务院下发了《低空空域管理改革指导意见》，意味着我国低空通用航空产业将迎来一个新的发展阶段。在通用航空中，低空物流是最具前景的通航应用业态之一，因此对其核心业务运营系统的研究与认识具有重要的现实意义。建立与通用飞行器飞行状态相关的通航物流配载效能优化模型，同时利用在遗传算法基础上经过算子与流程改进的PSGA算法对模型进行求解，不仅较好地提高了模型求解的效率与精度，也能够使配载模型和算法模型在通航物流企业业务运营中获得更好的实践意义。

关键词：通航物流;PSGA;AF因子;效能优化

中图分类号：F560   文献标识码：A   文章编号：1007-2101（2019）05-0101-08

一、引言

通航物流配载网络体系的广域性、体系运营的扁平性、地面基础设施的密集性以及网络关联的复杂性等特性是其区别于传统航空物流配载网络的特性，基于这些特性的研究将有助于我们进一步深入了解通航物流的运行特点，完善我们对通航物流网络体系和功能的构建。

近年来，随着低空空域领域改革方向的逐渐明晰，对通航物流领域的研究也慢慢丰富起来，但总体来说在内容与研究领域的多样性上还需进一步丰富。当前研究的主要方向集中于大型公共枢纽航空网络，特别是公共航空运输网络的货运配载优化、货物仓储管理及航班调度优化等领域。

杨忠振等研究了顺丰的枢纽网络快递线路优化问题;李程利用多元回归和灰色GM（1，1）模型预测了民航货运总量的变化过程;李烨研究了枢纽航空公司的运输效率问题;邹嘉唯等利用CCR模型和SBM模型研究了区域枢纽航空物流运营企业的效率问题。这些研究主要侧重大型航空货运不同系统阶段的效率评价。卜祥智研究了有空箱条件下的集装箱仓位分配问题并进行了仿真求解;李国等研究了Hadoop分布式文件系统的存储效率优化问题;谷雨哲使用ExSpect软件进行了花卉物流运输的仿真研究;唐少勇使用随机时间Petri网分析模拟了物流出港流程，對物流流程进行了仿真优化;张海峰利用Witness仿真软件对枢纽航空物流集散中心的内部流程进行了模拟仿真和效率优化;C Lee，HC Huang等使用有色Petri网对航空货运出港系统流程进行了效率研究;这些研究主要集中于航空货运节点的流程与效率仿真，研究过程基于仿真软件计算、应用层面的研究较多。Yi Tao和Ek Peng Chew等研究了航空货运承运人与托运人之间的最优定价博弈过程;Thijs Boonekamp等建立了基于货运体量与数量的货运网络关联模型;Qiang Gong等利用重力模型研究了国际航空货运的动力学机制和主要影响因素;Lucy Budd等探讨了全球航空货运体系中货运专机的角色与贡献率;Jafar Rezaei等提出了以成本和重量等为关键绩效指标（KPIs）的集装模式选择优化模型;Y Bai等探讨了航空货运出口货物处理速度的影响因素;Jiang等进行了区域枢纽机场的货运功能与区域铁路货运功能的优劣势研究。以上研究的侧重点大多是大型枢纽机场的航空货运网络，针对中小型机场和中小型货运专机网络的研究还比较少。

由此可见，当前关于航空物流运输网络和体系建设的研究大部分集中于大型公共航空运输体系和枢纽机场的航空货运及配载研究，对于适合中小型机场的航空物流运输体系建设研究相对较少。由于通航物流具有高频、多次、小批、低空的特点，因此通航物流运输体系与模式有别于传统航空运输，需要更多针对性基础研究为通航物流发展提供理论基础。此外，大多数大型航空货运优化问题研究关注的重点集中于时间、市场、流量、路线等宏观外部因素对优化目标的影响，而对飞机自身的性能指标、飞行模式选择以及飞行环境约束等内部微观因素对物流优化过程的影响分析研究较少。通航物流的载运平台一般为几吨或十几吨级的中小型通用飞机，飞行器和飞行状态的微观变化在很大程度上决定了通用飞机执行航空货运任务的效能水平，笔者从通航飞行器飞行状态和飞行环境中的几个主要因素入手，从飞行高度、飞行速度、空气密度、大气压力、燃油消耗上来考察通用飞机物流配载的最优状态。通过建立物流配载与飞行距离的双目标优化模型，研究探索通航物流过程在调整飞行状态和飞行参数条件下的最佳系统配载模式;同时通过使用在机制与算子上经过改进所形成的PSGA新型遗传算法建立算法模型，使算法的寻优过程效率更高，效果更好，使模型设计与算法改进更具备实践应用意义。

二、改进遗传算法

（一）基本遗传算法

遗传算法（GA）模拟了自然界普遍存在的物竞天择适者生存的原则，属于一类进化智能算法。其主要用于解决工程与应用中无法求得精确解的复杂NP问题。在模拟自然界生物进化过程中，选择、交叉、变异机制对问题的解空间进行优化搜索，使各代种群中的个体评价水平不断趋于最优，以至找到能够满足模型需求或最接近理论问题最优解的近似最优可行解。遗传算法的核心步骤包括：设计种子结构、生成种群、选择操作、交叉操作、变异操作、代际迭代，算法流程如图1所示。

如图1所示，首先根据问题的特点设计种群个体的构成，个体构成有多种形式，对于数值型个体，常用的为二进制结构。之后，根据种群规模生成初代个体的种群，同时根据预设的选择概率选择需要交叉的优秀个体;在选择个体后，根据交叉位置和预定的交叉概率对种子进行交叉，一般为将两个个体的部分基因片段进行互换形成交叉后的新种群;新的种群产生后，以预设的变异概率和选定的随机变异位置对种群的个体进行变异操作，将个体的一个或多个基因片段编辑后放回，最后按预定种群规模确定新一代个体，经过多次迭代后判断是否达到预定条件或阈值以确定算法的有效性。

（二）遗传算法改进

遗传算法为难以精确求解的很多现实工程应用NP问题提供了一个能够获得满足实际需求的近似最优解的途径，相较于其他NP问题算法，它在可行解空间中有较强的全域搜索能力，为获得更好的近似最优解提供了更大概率，同时他在进行种群内遗传操作时具有一定的并行运算能力，具有较强的鲁棒性。但传统的遗传算法也具有一定缺陷，例如：遗传算法需要对求解问题进行编码求解，一个遗传编码代表一个遗传操作个体，当求解问题的求解参数较多或对问题求解的影响因素较多，遗传编码的构造也就越为复杂，遗传个体的操作过程也变得越发复杂，求解过程和运算规模会快速上升，进而影响求解效率;遗传算法一般拥有三个遗传操作算子，在单位个体上需要至少操作三次，所以当遇到规模较大的求解问题或种群规模较大时，会使算法运行时间上升，效率下降;遗传算法的搜索广度大，但深度搜索能力不足，易于过早陷入局部最优解而影响算法后期的运行效率和最终求解效果;算法效果与遗传算子的概率选择经验因素较多，需要较多的实验过程选取更好的概率组合。

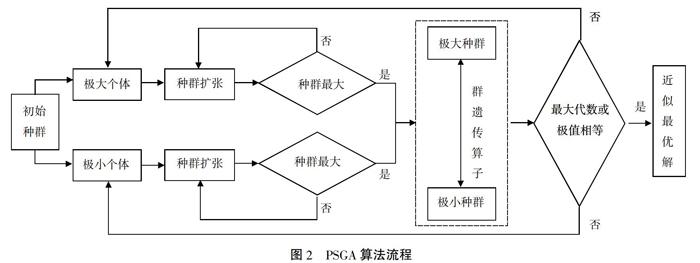
基于上述遗传算法的特点，笔者对传统遗传算法的流程与算子进行了改进，在借鉴杂草算法的基础上，提出一种新型PSGA变种群极搜索遗传算法。PSGA算法是在传统遗传算法的单种群进化机制上引入了个体繁殖策略，使单种群中的优秀个体有机会形成自己的种群，同时借鉴杂草算法中的种子计算方法，使越优秀的个体繁殖能力越强，不断淘汰劣等个体和劣等种群，最终使种群收敛于最优个体和最优种群。在PSGA算法中，取适应度值最大个体和适应度值最小个体作为各代中的元体或“两极”，按照不同的散布概率进行独立种群扩张，以最大适应度个体为元体的种群散布概率较小，以最小适应度为元体的种群散布概率较大，散布概率随代数变化和种群总体适应度水平变化而适时动态调整和收敛，进而在各代中保证在问题的可行解空间中进行全局搜索的同时亦可同步完成对潜在优秀个体的深度搜索;另一方面，在各代中，种群之间的遗传信息通过遗传算法进行信息交流，通过交叉和变异机制提升优秀基因片段的普及深度和优秀个体的出现概率，提升种群适应度水平的收敛效率，进而保证算法在搜索中的执行效率。PSGA算法执行流程如图2所示。

三、考虑飞行状态的通航物流配载效能建模

（一）飞行状态影响因素分析

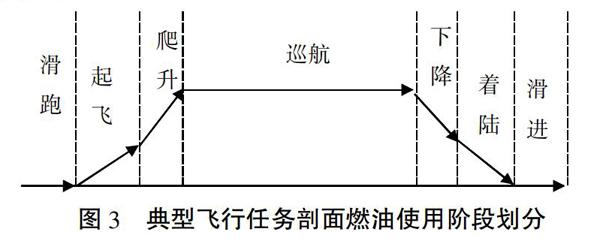
低空低速环境是大多数通用飞机的应用场景，一般通用飞机的任务高度不会高于6 000米，大多数任务是在1 000米～3 000米左右的低空空域。在低空环境下，空气密度大，对流天气多，飞机飞行高度与飞行速度的选择对飞行状态和飞行效能关联度较大;同时不同高度气压不同，发动机的燃油效率也不一样，同样的货运量所需携带的油量也会不同，也需要作出相应的调整，进而影响配载效能的大小;此外，飞行速度与飞行姿态的不同组合也会在不同程度上影响货运配载的效果。在通航物流任务过程中，包含了不同的飛行阶段（如图3所示），不同的飞行阶段会有不同的飞行策略，包括速度、高度、迎角等参数的不同组合。例如，在起飞与爬升阶段，飞机需要爬升到一定的巡航高度，就需要完成不同的飞行动作，经历不同的飞行状态，这其中飞机的发动机输出功率、燃油效率、姿态角和升阻比等多个参数都在不断变化，这些变化组合决定了飞行状态的效能水平;即使在同一飞行阶段，采取不同的飞行姿态，采用不同的参数组合也会给飞机的耗油率和航程等效能水平带来显著影响，进而直接或间接地影响飞机整体配载经济性。

由图3可知，通航飞机飞行各阶段中，巡航状态占据了主要的飞行状态。因此，为便于问题研究，笔者所探讨的效能优化问题为巡航阶段的通航配载效能优化。

（二）通航物流配载效能模型

通航物流配载的经济性与通航飞机在执行任务时所处的飞行状态关系密切。笔者将以通航物流配载效能为目标，以飞行高度、飞行速度、货运量、燃油质量、大气压强以及通用飞机自身的设计飞行特性为主要考察因素，建立通航物流配载系统经济性能模型;同时依据前述PSGA新型改进遗传算法框架设计遗传算子和扩散函数，为使用PSGA搜寻最优飞行状态和最优配载效能建立算法模型。

1. 配载效能模型。本文讨论的配载效能模型考虑了任务机型的飞行状态与基本飞行特性，以货物配载与燃油配载平衡和飞行里程远近双指标构建的综合模型。根据任务机型特性和状态建立通用飞机物流配载综合效能水平模型为：

其中，Feco为通用飞机的综合状态效能水平指数，Ml′、Mp、Ms、Mmax分别为某型通航飞机的燃油载量、飞机空重、飞机商载和飞机满载重量，n为执行满载任务的机队规模，KAB为由任务点A到通航飞行所能到达的最远任务点B的距离，？琢、？茁为配载系数，？琢>0、？茁>0，令？琢+？茁=1。

KAB反映了任务载机的内部特性和内部状态，其自身飞行参数和环境参数决定了这种内在状态水平的高低程度。设飞机的任务飞行高度为h、飞行速度为v，所处飞行高度的空气密度为？籽h，大气压力为P，飞行高度的气温为Ch（通用飞机的飞行速度一般较低），同时为便于问题研究，假定大气为理想气体，在接近地表时0℃下空气密度为1.293kg/m3、1标准大气压为1.013 25Pa，0海拔下，海平面温度为15℃，10 000米高空温度为-50℃，则可得不同高度下气温变化为：

其中C0为地表基础温度。

根据理想气体状态方程和气体摩尔量公式得到的空气密度随大气压强的变化规律为：

由此可得通用飞机的飞行高度随大气压力调节的关系式为：

Ph=e5.25885ln（288.15-0.0065h）-18.2573（3）

（2）（3）式体现了飞机的外部环境因素的影响规律。

设飞机在滑跑阶段的起飞重量为Mb，巡航阶段的重量变化量为M，滑进阶段的飞机重量为Mf，单位油耗下飞机巡航的里程为Kp，巡航阶段从A点到B点的飞行总里程为KAB，巡航阶段的飞行速度为v，飞行时间为t，则有：

由此可推得通用飞机的巡航阶段总里程为：

设通用飞机在巡航阶段自身所受升力为L，推力为T，阻力为D，升力系数和阻力系数分别为CL和CD，飞机的飞行姿态迎角为？兹，机翼面积为S，则根据空气动力学方程有：

进而可知在由飞机自身特性所决定的内在状态参数和飞机所处飞行状态所决定的外在状态参数的作用下，通用飞机在巡航阶段飞行距离的状态表达式为：

以上里程表达式反映了飞机的巡航速度、机翼面积、飞行姿态、状态系数等内在影响因素对通用飞行里程变化的影响规律。由此可见，Feco是对通航物流配载任务中飞机内外部影响因素整体协同的综合效能反映，它反映了各类状态因素对通航物流配载效能水平的作用效果。

2. PSGA算法模型。根据以上配载效能水平的建模和前述PSGA算法流程，可建立通航物流配载效能优化的PSGA算法模型。设PSGA算法的目标函数为：

Fmax=max{Fleco}

其中，Fleco={Fe1，Fe2，…，Fei…}，其飞行状态环境约束为：

以目标函数作为PSGA算法的个体适应度函数，种群扩张的最大代数为itermax，当前代数为iter，个体当前适应度为ad，本代中最大适应度为admax，最小适应度为admin，当前代初始个体为adini。

在传统的遗传算法中，种群的优化过程是在种群规模相等的基础上进行的，遗传操作过程决定了个体的优化水平，个体不具备对解空间更强的探索性。因此，在PSGA算法中，为了优化个体能够在空间探索深度与探索广度上能力更强，加入了适应度调和机制。通过“适应度调和因子（AF）”使种子个体能够进行独立的空间探索，在各代际间根据种群整体的空间分布状态自适应地进行全局或局部搜索，有效增强最优解的搜索水平和算法执行效率。设PSGA算法的AF因子为F（？琢，？茁），则有：

四、通航物流配载实例研究

根据上述通航物流配载效能模型和PSGA算法种群优化模型，笔者通过以某型号通航货运飞机的自身特性与实际运营状态为研究对象，探讨通航物流配载效能水平的优化过程。

根据以上配载状态设计和算法参数设置，在Matlab8.3软件环境下进行算法实现和运行分析。

由图4分析极小值种群在迭代中的进化过程。图4的左右两边分别是初始第1代和35代迭代后的极小值种群三维空间分布图，图4中的三角形代表一个满足配载效能优化的可行解。图4中可见第1代中的可行解在解空间中分布较为分散，种群个体散布较广，这是因为初代的适应度最小值最小，空间广度的探索能力最强，而经过多代迭代后适应度值逐渐提升，进而在右图中显示为种群分布逐步聚集，空间广度的探索能力减弱，空间深度的探索能力增强，适应度值水平逐步向最大值靠近。

圖5是极大值种群四个不同进化阶段的个体分布三维空间切面图。图5中星号代表一个可行解。由图5可见，极大值种群的探索空间分布要比极小值探索空间小很多（从图4中星号聚集区域的分布空间与同图中实心三角形个体的分布空间对比可见），这是因为经过AF因子的调和，各代中的最优个体更加注重近似最优解周围空间的深度探索，通过三个坐标轴数值范围的变化方向也可看出这一特点。图5中的四个切面图（按由上至下、由左至右顺序）分别为极大值种群进化的第1代、第5代、第11代和第35代的个体分布情况。在初始第一代中三坐标轴的取值范围与后三图差异较大（例如横坐标轴取值范围从第1代的（3 498，3 504）到第5代的（856，864）），这是因为初代中的种群个体适应度普遍偏低，在经过进化操作后，最优个体的探索空间范围基本稳定下来（由5、11、35代切面图的三坐标轴取值范围可见，特别是第11、35代的取值范围基本固定，这说明最优个体适应度取值范围已基本收敛稳定）;同时，我们还可以看出各代中个体的分布既有一定程度的聚集性又有一定的发散性，通过适应度因子的调和，PSGA算法在强调深度探索的同时还保证了一定程度的广度探索。

图6为在种群规模20、选择概率0.6、交叉概率0.6、变异概率0.1、最大进化代数50的同环境参数下PSGA算法（实线）与遗传算法（点线）运行10次取平均值的优化过程比较图。由图6的两幅图可看出PSGA算法的适应度值跨度更大，探索的空间范围更广，同时在收敛速度上PSGA算法更快，遗传算法经过35代找到最好个体为536.476 3，而PSGA算法经过10代找到最好个体为537.931 0。因此，在综合性能和寻优过程比较来看，PSGA算法的效率更高，寻优效果更好。

根据以上运行分析可知，使用PSGA算法求得的用某型号通航货运飞机执行货运任务所能达到的最优配载状态为：货运配载965.130 1公斤、航油配载836.919 9公斤、巡航高度保持在2 212.553 0米、高空巡航保持平飞姿态、巡航速度维持在59.785 8公里/小时，以该配载状态飞行最远航程为1 442.904 6公里，最优配载效能指数为537.931 0。

五、结语

综上所述，笔者使用在传统遗传算法基础上经过流程和算子改进的新型PSGA算法，对通航物流的配载状态进行了探讨，同时对通航物流效能水平的优化问题进行了分析与实践。在研究过程中，笔者考察了与飞机自身特性和飞行状态相关的内外因素对通航物流配载状态的影响，建立了飞机的配载效能模型和优化算法模型，之后又以运营中的通用飞机实际参数特性为例对模型进行了验证，求得在一定飞行内外部环境参数约束下，通航物流任务最优配载效能水平所需要的最佳配载状态，为通航物流企业进一步优化管理流程、提升通航运营效率进行了有意义的探索。

参考文献：

[1]杨忠振，于述南，陈刚.混合式航空货运网络优化[J].交通运输工程学报，2016（1）：103-114.

[2]李程.航空货物运输优化运营若干问题研究[D].上海：东华大学，2015.

[3]李烨. 航空公司效率评价的改进DEA模型及应用[D].大连：大连理工大学，2016.

[4]邹嘉唯，徐月芳. 基于Super-SBM模型的我国航空运输企业运营效率评价[J].现代商业，2017（32）：23-26.

[5]卜祥智.基于收益管理的集装箱班轮舱位分配随机模型研究[D].成都：西南交通大学，2005.

[6]李国，李汶晓，徐俊洁. 航空货运中海量小文件的存储优化[J].计算机工程与设计，2018.

[7]谷雨哲. 云南花卉航空运输物流流程优化与仿真[J].物流技术，2014（19）：168-170.

[8]唐少勇. 基于PETRI网的航空货运出港流程仿真优化研究[D].天津：中国民航大学，2015.

[9]张海峰. 基于petri网的南京邮政速递物流集散中心流程优化研究[D].天津：天津科技大学，2014.

[10]Lee C，Huang H C，Liu B，et al. Development of timed Colour Petri net simulation models for air cargo terminal operations[J]. Computers & Industrial Engineering，2006，51（1）：102-110.

[11]Tao Y，Chew E P，Lee L H，et al. A capacity pricing and reservation problem under option contract in the air cargo freight industry[J]. Computers & Industrial Engineering，2017.

[12]Boonekamp T，Burghouwt G. Measuring connectivity in the air freight industry[J]. Journal of Air Transport Management，2016.

[13]Gong Q，Wang K，Fan X，et al. International trade drivers and freight network analysis - The case of the Chinese air cargo sector[J]. Journal of Transport Geography，2017.

[14]Budd L，Ison S. The role of dedicated freighter aircraft in the provision of global airfreight services[J].Journal of Air Transport Management，2016.

[15]Rezaei J，Hemmes A，Tavasszy L. Multi-criteria decision-making for complex bundling configurations in surface transportation of air freight[J]. Journal of Air Transport Management，2017（61）：95-105.

[16]Bai Y，Wei-Hong L I. Capability evaluation of air cargo export handling system using Stochastic Petri Net[C]// International Conference on Logistics Systems and Intelligent Management. IEEE，2010：1589-1593.

[17]Jiang C，Zhang A. Airline network choice and market coverage under high-speed rail competition[J].Transportation Research Part A Policy & Practice，2016，92：248-260.

Optimization of General Aviation Logistics Stowage Based on PSGA-improved Algorithm

Zhang Hao

（1.Management School，China University of Mining and Technology（Beijing）， Beijing 100083， China;

2.CAIGA North China Aircraft Industg Co.， Ltd. Hebei Shijiazhuang 051430， China）

Abstract： In 2012， the State Council issued the Guidelines for the Reform of Low Altitude Airspace Management， which means that China's low-altitude general aviation industry will usher in a new stage of development. In general aviation application， the most promising industry and potential application area is the general aviation logistics， so the research and understanding of the general aviation logistics operating system has more practical significance. This paper established the optimization model of general aviation logistics stowage efficiency related to the flight state of general aircraft. At the same time， the model is solved by PSGA algorithm based on Genetic Algorithm by improving operator and process， which can improve the efficiency and accuracy of model solution， and it can also make the loading model and algorithm model obtain better practical significance in the business operation of general aviation logistics enterprises.

Key words： general aviation logistics， PSGA， AF-factor， performance optimization