基于NSGA-II和博弈理论的主动式配电网多目标优化调度

谢千焱，李凤婷*，丁 坤，辛超山

(1.新疆大学 可再生能源发电与并网技术教育部工程研究中心，新疆 乌鲁木齐 830047； 2.国网甘肃电力有限公司 风电技术中心，甘肃 兰州 730050； 3.国网新疆电力有限公司 经济技术研究院，新疆 乌鲁木齐 830002)

配电网中分布式电源的“就地消费”，能有效减少多级电力变送所带来的损耗及相应的电网建设投资，减少对大规模电力生产的依赖[1-2].主动式配电网能增强配电网吸收分布式电源的灵活性，还有削峰填谷功能.因此，优化主动式配电网电源调度，保证电网安全、经济、高效运行，是目前主动式配电网研究的核心问题[3-6].

分布式电源的参与导致主动式配电网优化调度计算是非线性的，因此要采用一种优化技术实现非线性计算.针对含分布式电源的主动式配电网优化调度问题，文献[7]以分布式电源消纳最大为目标，对配电网进行规划，但没有考虑主动负荷的灵活配合.文献[8]考虑居民用电意愿及习惯制定了主动负荷需求响应方案，但运用的是经验模型没有使用优化算法.文献[9]提出了基于预测控制的配电网多时间尺度有功出力调度策略，但分布式间歇性电源的预测精度还有待提高.文献[10]研究了主动式配电网经济函数的优化，并对电源结构进行了规划，但目标函数单一没有考虑多方协同.

针对主动式配电网研究中存在的上述问题，笔者提出一种主动式配电网多目标优化调度方法.该方法利用主动负荷的灵活性，以含分布式电源的主动式配电网综合运行成本最低和负荷方差最小为优化目标，在经济运行的基础上，实现削峰填谷、改善负载曲线.采用改进的非劣排序遗传算法(NSGA-II)与博弈论相结合的方法优化求解，结合算例进行仿真验证.

1 负荷数学模型

1.1 不可控负荷

不可控负荷(uncontrollable load, 简称UCL)功率变化区间小，无法进行灵活调控.此类设备用EUCL表示，其特征描述如下

(1)

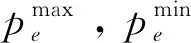
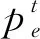
(2)

根据式(2)，UCL在用电时间内用电功率存在上下限，用电时间外无功率消耗.

1.2 可转移负荷

可转移负荷(transferable load,简称TL)用电比较灵活，用电时间内总用电量固定，可灵活调控，具备转移能力.此类设备用ETL表示，其特征描述如下

(3)

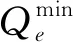
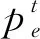
(4)

根据式(4)，TL在用电时间内用电功率存在上下限，用电时间外用电量要保证最低需求.TL可灵活调整工作时间，在满足工作要求的基础上适当调度负荷.

1.3 可中断负荷

可中断负荷(interruptible load,简称IL)在工作期间可随时断开， IL的中断时长受用户舒适度约束.此类设备用EIL表示，其特征描述如下

(5)

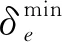
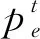
(6)

1.4 集总模型

负荷侧用集总模型表示.按工作时间序列，结合用户消费习惯，依据用电统计特征得到负荷工作状态概率矩阵S及其相关表达式如下

(7)

(8)

(9)

其中：sit为第i种用电负荷在t时段的工作概率；pit为第i种用电负荷在t时段的功率，UCL的pit满足式(2)，TL的pit满足式(4)，IL的pit满足式(6)；m为实际用电设备的数量；T为统计时间内的时段数；Pin为负荷i的额定功率.

2 主动式配电网多目标优化调度模型

配电网的电能主要来自主网的购电及自身的分布式电源.分布式电源一般为风电机组和光伏发电系统，鉴于新能源特性，配电网内会增设一定容量的微型燃气轮机(简称微燃机).对配电网接入的新能源，通常将其最大程度利用，此时会采用最大功率点跟踪模式[11-13].在保证供电可靠的前提下，为提高配电网负荷率、实现削峰填谷及经济运行，笔者选取运行成本最低和负荷方差最小为优化目标，以主网联络线传输功率和微燃机的发电计划为调控对象，建立多目标优化调度模型.

2.1 目标函数

(1) 配电网运行成本的最小化

通过优化主动负荷用电计划、分布式电源的出力及主网联络线功率，使配电网区域综合运行成本最低，其目标函数为

(10)

其中：CFU(PDG(i,t))为燃耗成本；COM(PDG(i,t))为分布式电源的运行成本；NDG为分布式电源的数量；PDG(i,t)为分布式电源i在t时段的输出功率；Pgrid(t)为t时段主网联络线功率；Ploss(t)为t时段配电网损；ωt为t时段购电电价，分时电价情况如下：09:00—23:00为0.595元·(kW·h)-1，23:00—09:00(次日)为0.315元·(kW·h)-1.

对于可再生能源机组，由于无燃料消耗，其燃耗成本可忽略不计.对于微燃机等分布式电源，可对其出厂测试的燃耗成本数据进行拟合，得到相应的燃耗成本系数.微燃机燃耗成本的表达式为

(11)

其中：ai，bi，ci分别为微燃机燃耗成本的2次、1次及常数项系数.

分布式电源的运行成本及出力满足如下正比例关系

(12)

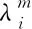
电流在电力网络中传输时，电线内阻消耗的功率称为电力网损.主要电压等级的容量、传输距离及对应网损率[14]如表1所示.

表1 主要电压等级的容量、传输距离及对应损耗

(2) 负荷方差的最小化

在基础负荷(不可控负荷)不变的前提下，对主动负荷进行优化调节，使系统综合负荷的方差最小.负荷方差目标函数为

(13)

(14)

2.2 约束条件

(1) 系统功率平衡

系统功率平衡约束为

(15)

(2) 系统备用容量

系统备用容量约束为

(16)

其中：PL(t)为系统在t时刻的总负荷功率，θt为系统备用率.

(3) 分布式电源出力

出力功率约束为

(17)

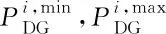
出力爬坡约束为

(18)

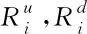
(4) 设备限制

变压器容量约束为

(19)

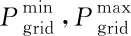
网络节点电压约束为

(20)

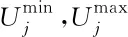
支路传输功率的约束为

(21)

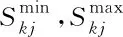
3 基于NSGA-II和博弈论的优化计算方法

建立的多目标优化模型中含有多种等式与不等式约束，在多目标优化计算中很难通过权值的设置转换为单目标.一般来说，在优化求解过程中，各个目标函数相互制约，得到的某个最优解难以使所有目标值均处于最优状态.单一采用遗传算法只能求得一个非劣解集合(帕累托(Pareto)解).根据博弈论中的纳什均衡可知，存在唯一均衡偶，使目标函数达到均衡状态.笔者首先使用NSGA-II计算两个目标函数在变量约束区间内的极大值，然后利用纳什均衡理论，结合目标函数的极大值确定均衡状态，最后求唯一均衡偶.

3.1 遗传算法

针对建立的多目标优化模型，用NSGA-II求目标函数的极大值.算法流程如图1所示.

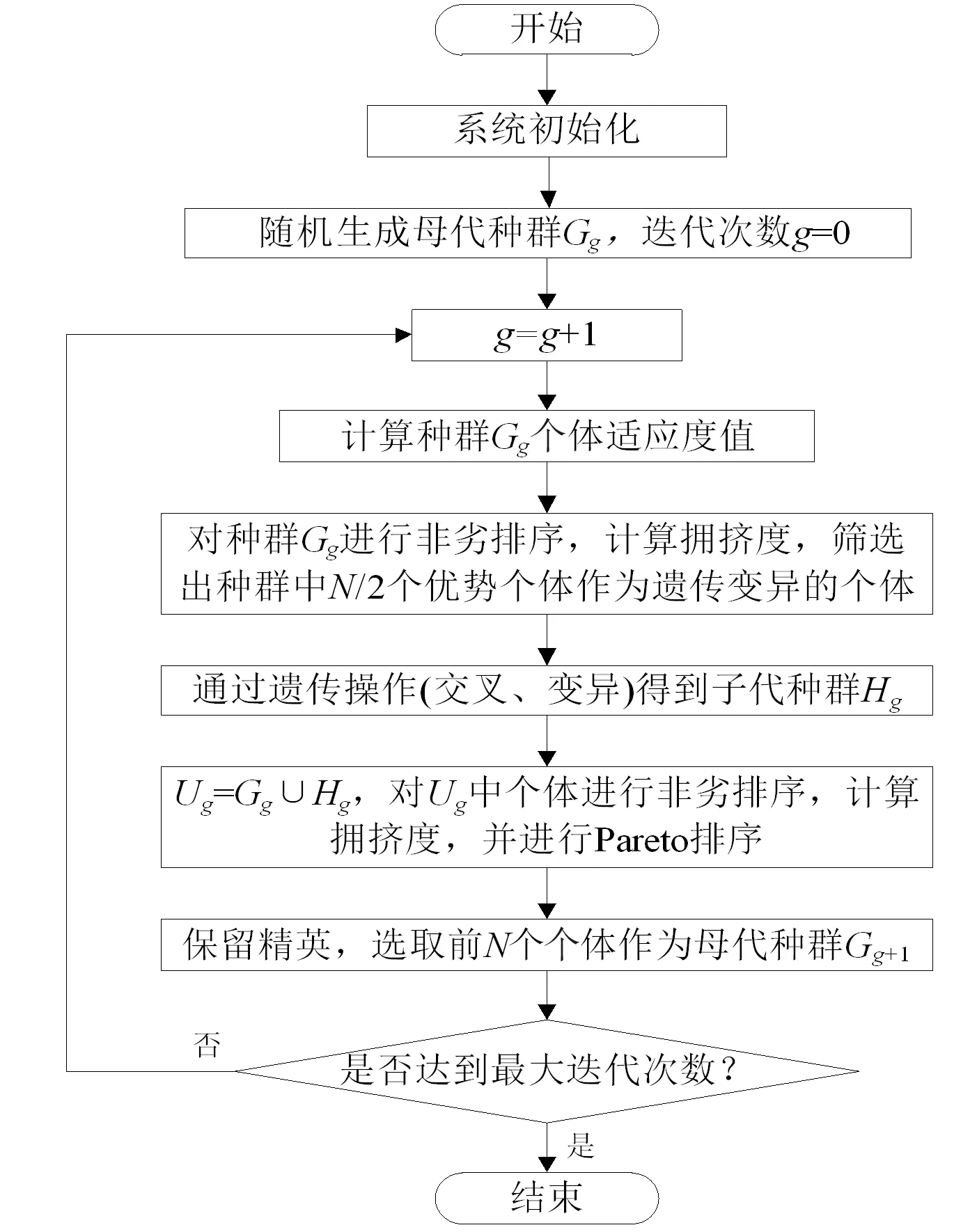
图1 算法流程

3.2 博弈论及寻优方法

博弈论是研究竞争者为争取最大利益如何做出决策的数学方法[15-16]，目的是使各主体间取得平衡，以最大化收益.笔者使用纳什均衡构建均衡优化模型.

综合运行成本为

p=f1(x1,x2).

(22)

负荷曲线方差为

q=f2(x1,x2)，

(23)

其中：x1为微燃机出力，x2为主网联络线传输功率.

F1(x1,x2)=f1(x1,x2)-pmax，

(24)

F2(x1,x2)=f2(x1,x2)-qmax，

(25)

其中：pmax，qmax可在遗传算法中求得.

设

I(x1,x2)=F1(x1,x2)·F2(x1,x2)，

(26)

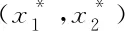
I(x*)=I(x)max.

(27)

4 算例分析

4.1 算例描述

假定系统内有1 000用户、 3座工厂.设系统中接入1 500 kW的风电机组(WT)、2 000 kW的光伏电站(PV)及微燃机组(MT)，机组具体参数如表2所示.根据某地区实际用电负荷构成，得到负荷信息如表3所示.

表2 机组参数

表3 负荷信息

根据实际电网得到的风电、光伏与负荷的功率曲线如图2所示.

图2 风电、光伏及负荷的功率曲线

4.2 算例仿真

依据负荷状态概率矩阵S，运用Monte Carlo模拟法产生1 000个用户的用电负荷数据，然后进行模拟仿真.

选取两种不同的场景对该文方法进行仿真验算.

场景1：不进行主动负荷调度.

场景2：使可灵活调控的主动负荷(定时电饭煲和部分电动汽车)参与日前调度.

将场景2的优化问题用该文方法求解，得到的博弈结果为

f1=10 295 994.72，f2=1.184 0.

均衡解所对应的日前最优调度方案如表4所示.日前机组发电计划如图3所示.

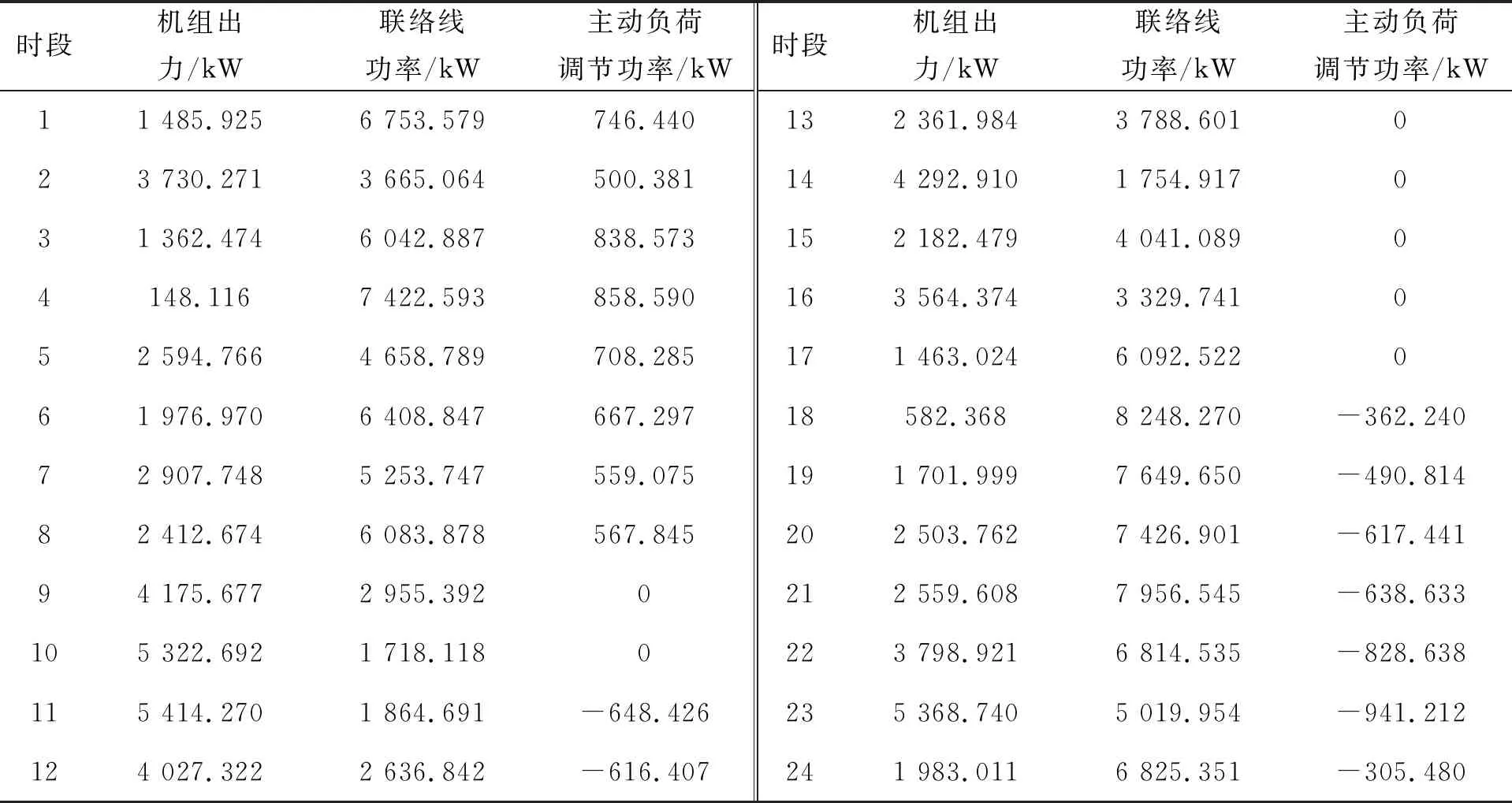
表4 日前最优调度方案

图3 日前机组发电计划

从表4和图3可以看出，在低电价时段，即23:00到次日09:00，微燃机的发电成本较高，此时应进行主网输电以满足负荷要求.在高电价时段，即09:00至23:00，电网购电成本增加，应大幅减少主网购电，此时微燃机应作为主要电源.该调度方案明显减小了系统综合运行成本，具有一定的经济效益.

对比分析两场景下的负荷功率，情况如图4所示.分析两场景下的负荷特性指标，结果如表5所示.

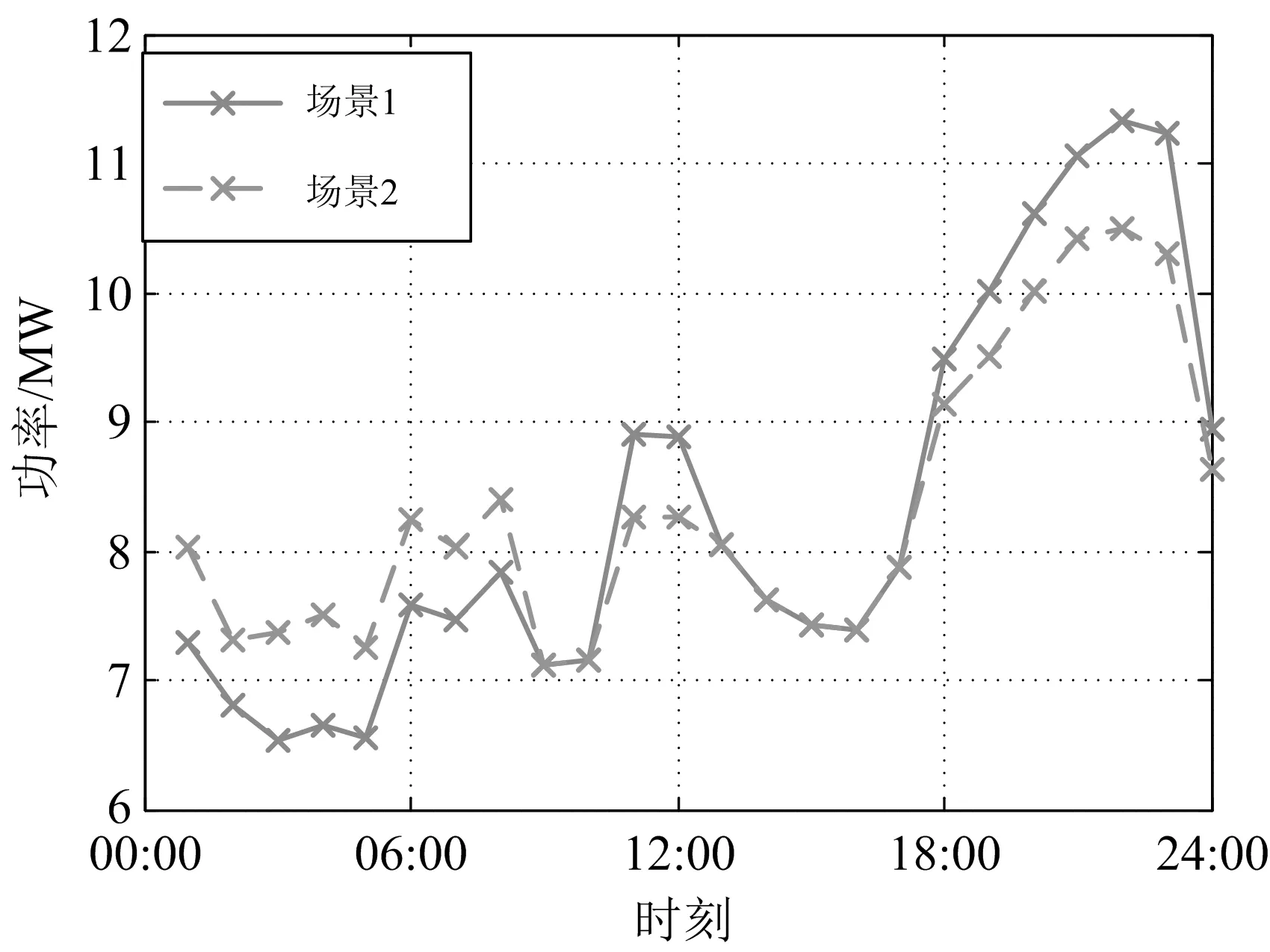
图4 负荷功率对比

表5 负荷特性指标

场景最大负荷功率/MW最小负荷功率/MW平均负荷功率/MW峰谷差率/%111.3326.5338.32742.35210.5047.1188.32632.24

从图4和表5可以看出，当使场景2中的主动负荷参与调度时，主动负荷由10:00—13:00及17:00—24:00的负荷峰阶段，转移至1:00—9:00(次日)的负荷谷阶段，负荷特性明显改善，峰谷差率下降至32.24%，表明该调度方案有明显的削峰填谷作用.

5 结束语

笔者从多目标优化的角度研究了分布式电源与主动式负荷的优化调度问题.通过负荷需求计算负荷概率矩阵，在此基础上，以含分布式电源的主动式配电网综合运行成本最低和负荷曲线方差最小为优化目标，建立了含分布式电源的主动式配电网多目标优化调度模型.采用NSGA-II与博弈论相结合的方法优化求解，结合算例进行仿真验证.仿真结果表明该方法在保证系统经济运行的同时，能有效利用主动负荷的灵活性降低系统的负荷峰谷差.