面向海洋能综合利用的港口用电策略研究
2019-09-16刘华锟李相达
彭 云,刘华锟,李相达
(大连理工大学 建设工程学部,大连 116023)
随着港口能源危机和环境污染问题日益突出,传统燃油、煤电供能的能源结构越来越难以满足绿色港口发展的需要。为此,世界各主要港口积极推进能源结构转型、提高能源利用率,例如,西班牙Ribadeo港口通过建造海洋能发电站来实现港口用能的自给自足[1]。然而,以海洋能为代表的清洁能源,其发电功率受自然环境影响较大,具有波动性和随机性等特征,海洋能供电需调配市电,形成多能互补的能源结构。因此,探究面向海洋能综合利用的港口多能互补的用电策略显得尤为重要。
国内外有关港口用电策略的研究主要集中在利用风电、光电等清洁能源供电和使用岸电等方面。例如,Anna Maria Kotriklan等[2]通过仿真得到,米特里尼港的船舶总能源需求可以由4台1.5 MW的风力涡轮机和一台5 MW的光伏发电机提供;俞晓[3]研究发现,在油价高于5 092.59元/t或电价低于0.83元/kWh时,使用岸电的成本将低于使用重油发电的成本,船舶节能率可达58.22%。
国内外针对海洋能综合利用的研究主要集中在宏观政策和海洋能发电技术等领域。麻常雷等[4]提出了我国开发利用海洋能的相关政策建议。N. Khan等[5]研究了潮汐能、波浪能等能源的发电潜力。陈凤云[6]研究了海洋温差发电系统的热力循环方式问题。Babarit等[7]研究了海上风能、波浪能与陆地电网联合为海岛居民供电的电力存储系统规模问题。Fusco等[8]研究了风能和波浪能资源的优化组合对电力功率输出可变性的影响。
综上,已有针对港口用电策略的研究多从利用风电、光电等清洁能源供电和使用岸电两方面来分析港口的环境效益和经济效益,针对海洋能发电的研究多集中于技术层面,还需进一步将海洋能与市电并网,考虑海洋能供电的不确定性,确定港口的用电策略。为此,本文在分析海洋能供电不确定性的基础上,结合港口作业系统用电需求变化规律,构建了面向海洋能综合利用的港口用电多目标优化模型,实现环境和经济效益的最大化,为优化港口能源结构、合理开发利用新能源、绿色港口运营及能源调配决策提供理论依据。
1 港口用电策略多目标优化模型
本文在分析港口生产作业系统用电负荷和海洋能发电功率变化规律的基础上,考虑海洋能供电和传统市电的调配,构建港口用电策略的多目标优化模型,以港口用电成本最低、碳排放量最少以及电网资源利用率最高为目标,探究面向海洋能综合利用的港口用电策略。
1.1 模型假设
(1)不考虑国家扶持基金、输配电费及功率因数调整等对电价的影响;
(2)不考虑储电设备和国家对清洁能源发电的补贴政策。
1.2 模型构建
本文以码头用电总成本最低、全生命周期碳排放量最少和电网资源利用率最高为目标建立多目标优化模型,根据海洋能发电机组功率和港口负荷的要求,设置海洋能发电机组约束和港口用电功率约束。该模型不仅考虑海洋能发电在港区的直接碳排放,同时也考虑了海洋能发电在全生命周期的间接碳排放,包括海洋能发电设备在制造过程中产生的碳排放等。
1.2.1 目标函数
(1)用电成本最低
(1)
(2)全生命周期碳排放量最少
(2)
(3)电网资源利用率最高
(3)
式中:模型的决策变量为αi和βi,αi为各时刻的市电供电功率,βi为各时刻的海洋能供电功率;cf为市电峰时段电价,元/kWh,cp为市电平时段电价,元/kWh,cg为市电谷时段电价,元/kWh;tf为峰时段时刻集合{8,9,10,18,19,20},tp为平时段时刻集合{6,7,11,12,13,14,15,16,17,21},tg为谷时段时刻集合{1,2,3,4,5,22,23,24};b为海洋能发电电价,元/kWh;k1为市电的全生命周期碳排放系数,t/kWh,k2为海洋能发电的全生命周期碳排放系数,t/kWh,f1为用电成本,元,f2为全生命周期碳排放量,t,f3为公共网络资源利用率,η为海洋能发电的电网资源利用率。
由于目前国内外关于海洋能电价的标定尚未制定统一标准,本文参考邹健健等[11]对潮汐能发电电价的敏感性分析研究,确定海洋能电价b的计算公式为
(4)
bcon=10 000×Ccon×Q
(5)
bopr=10 000×Copr×Q
(6)
式中:bcon为海洋能发电设备的总建设成本,元;bopr为海洋能发电设备的年运营成本,元/a;Topr为海洋能电站的运营年限,a;Q为海洋能发电设备的装机容量,kW;t为海洋能发电设备的年发电时长,h/a;Ccon为海洋能发电设备的单位建设成本,元/kWh;Copr为海洋能发电设备的单位运营成本,元/(a·kW)。
1.2.2 约束条件
(1)机组约束。
各时刻海洋能发电功率有限,因此各时刻海洋能发电的供电功率不能超过该时刻的海洋能最大发电功率,即
0≤βi≤βimax
(7)
式中:βimax为i时刻海洋能最大发电功率,kW。
(2)功率约束。
为满足港口负荷的要求,各时刻的海洋能发电功率和市电购电功率之和应等于该时刻的港口负荷,即
Pi=αi+βi
(8)
式中:Pi为i时刻港口用电功率,kW。
1.3 模型求解
港口用电策略多目标优化模型选用Matlab中的Gamultiobj函数进行求解,获得包含200个非劣解的Pareto最优解集。基于模糊隶属度和方差赋权的方法选取最优解,目标函数的优化程度可以通过隶属度的大小来反映,求解步骤如下:
(1)计算最优解集中第k个Pareto解对应的第j个目标值的隶属度函数ukj
(9)
式中:N为Pareto解数目,M为目标函数数目,fkj为第k个Pareto解的第j个目标函数值,fjmax和fjmin为第j个目标函数值在优化过程中的最大值和最小值。
(2)采用基于目标函数隶属度方差的客观赋权方法
(10)
式中:ωj为第j个目标函数的权重。
(3)把隶属度加权和Fk作为对应第k个Pareto解的选择优先度
(11)
Fk的最大值所对应的Pareto解为该次优化的无偏最优解。
2 算例分析
2.1 算例背景

图1 港口负荷及海洋能最大发电功率Fig.1 The load of port and the maximum power generation of marine energy
在该算例中,本文对我国南方某码头2014年9月8日的用电负荷进行了分析,采用市电与海洋能联合供电的策略,选用潮汐能发电效率较高的双水库连接方案进行海洋能供电,应用前文提出的多目标优化模型,对1 d内各时刻的市电供电功率和海洋能供电功率进行优化,通过遗传算法求得市电供电功率和海洋能供电功率的帕累托最优解集,利用基于模糊隶属度和方差赋权的方法求得该码头1 d内各时刻的最优用电策略。该码头2014年9月8日的港口负荷曲线及海洋能最大发电功率曲线如图1所示。
2.2 输入参数
该码头所在城市的大工业电价由电度电价和基本电费构成,基本电费根据用电单位的最大需量和变压器容量来确定。同时该城市实施阶梯电价,用电时段不同,相应的电价也不同。该码头日最大负荷为2.7 kW,日总用电量为195.12 MWh,变压器容量为25 MVA,具体电价如表1所示。
海洋能年发电时长约为3 200 h[10]。海洋能电站装机容量每千瓦投资约3万元,年发电成本约为每千瓦0.470万元,设备建设期为2 a,运行期为15 a,则该码头海洋能发电电价为2.094元/kWh[11]。
根据《2015年中国区域电网基准线排放因子公告》[12],该码头所在的华东区域电网的全生命周期碳排放系数为0.811 2 kg/kWh;潮汐能发电的全生命周期碳排放系数为9.5~11.0 g/kWh[13],本文取值为10.0 g/kWh,即0.01 kg/kWh;海洋能发电装置仅有20%左右的满功率输出率,若发电站的装机条件满足满功率发电要求,则海洋能发电的电网资源利用率约为20%[14],因此式(3)中η值取为0.2。

表1 大工业用电阶梯电价Tab.1 The adder price of large industrial electricity in the city where the terminal is located
注:峰时段为每日的8~11时、18~21时,平时段为每日的6~8时、11~18时、21~22时,谷时段为每日的22时~次日6时。
2.3 结果分析
运用Gamultiobj函数对优化模型进行求解,并选择最优用电策略,确定最优用电决策下的各时刻市电供电功率和各时刻海洋能供电功率,结果如图2所示。
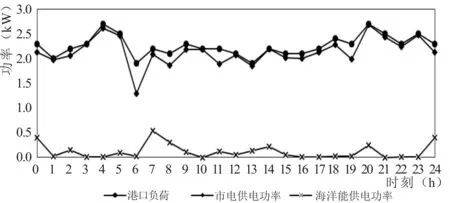
图2 b=2.094元/kWh,港口负荷-市电供 电功率-海洋能供电功率曲线Fig.2 The load of port-mains power-marine energy power, while b=2.094 yuan/kWh
图2表明,当海洋能电价为2.094元/kWh时,在最优策略下,1 d内的市电总供电量为184 957.2 kWh,海洋能总供电量为10 162.8 kWh,由于最优用电决策的海洋能用电量较少(仅占总负荷的11.08%),大部分电力供应仍来源于市电,因此全生命周期的碳排放量仅降低了5.14%,减排效果并不明显。由于海洋能电站的建设成本较高,因此海洋能发电的电价较高。通过采用浮运施工法等降低潮汐电站造价的措施,可使潮汐电站的建设成本降低25%~38%[15];由于潮汐电站的工程造价较高,因此延长潮汐电站的使用寿命可以有效较低电价,潮汐电站的使用期最长可达75~100 a[16];潮汐电站的不同布置形式,如加大潮汐涡轮机间距,采用潮汐涡轮机与岸上风力涡轮机共同布置的形式,可以提高潮汐电站的发电效率,降低运行成本10%~12%[17]。结合以上降低潮汐能发电电价的措施,根据1.2.1节中海洋能电价的计算公式,本算例中海洋能发电电价最多可降低35.6%,即降至1.351元/kWh。为研究海洋能电价的变化对用电策略的影响,本文对海洋能电价进行敏感性分析。经计算,当海洋能电价分别降低10%(1.885元/kWh)、20%(1.675元/kWh)、30%(1.466元/kWh)以及40%(1.256元/kWh)时,最优用电决策的港口负荷-市电供电功率-海洋能供电功率曲线如图3所示。
选取海洋能供电量、总用电成本、全生命周期碳排放量等指标,对比不同用电策略下的供电效果;根据我国的碳交易市场上的二氧化碳交易价格[18],本文选取二氧化碳交易价格为20元/t,计算了考虑碳交易的总用电成本,结果如表2所示。

表2 用电策略指标对比Tab.2 Comparison on indicators of power consumption strategies
表2结果显示,与全部使用市电进行供电相比,在使用海洋能和市电联合供电的条件下,当海洋能电价为2.094元/kWh时,由于海洋能电价过高,用电成本对使用海洋能的限制较大,最优供电策略下的全生命周期碳排放量仅降低5.14%;随着海洋能电价的降低,海洋能发电的使用量逐渐增多,减排效果逐渐提升,当海洋能电价降至1.256元/kWh时,在使用海洋能和市电联合供电的最优策略下,全生命周期碳排放量降低31.09%,减排效果明显。
考虑碳交易引起的二氧化碳排放成本,在不同的海洋能电价情况下最优用电决策的总用电成本随着海洋能电价的降低而增长,然而增长幅度逐渐减小,当海洋能电价低于1.466元/kWh时,总用电成本到达稳定水平。这一结果表明,当海洋能电价低于1.466元/kWh时,全生命周期的碳排放量降低率超过24%,减排效果明显,且考虑碳交易的总用电成本不再增长,因此,可以认为可接受的海洋能电价为不大于1.466元/kWh。
3 结论
本文首先建立了面向海洋能综合利用的港口用电决策优化模型,以环境效益、经济效益和电网资源利用率的最大化为目标,通过遗传算法求得帕累托最优解集;其次,运用基于模糊隶属度和方差赋权的最优解决策方法选出最优用电决策;最后,以我国南方某码头的实际用电情况为例,应用该模型对算例码头的用电策略进行优化。算例分析结果表明,使用海洋能和市电联合供电能够起到减排效果,当海洋能电价为2.094元/kWh时,由于电价较高,全生命周期的碳排放仅降低5.14%;当海洋能电价降至1.256元/kWh时,全生命周期的碳排放降低31.09%,最优策略的减排效果越明显。结合碳交易分析得,当前可接受的海洋能电价为不大于1.466元/kWh。
