一种基于博弈论的时序网络链路预测方法

刘 留 王煜尧 倪琦瑄 曹 杰 卜 湛

1(南京财经大学信息工程学院 南京 210013)2(南京理工大学计算机科学与工程学院 南京 210094)

许多现实世界的网络系统是非静态的，节点间的连接关系随时间动态变化，此类网络可由一系列包含时间戳的链路集合[1]表示.在动态网络研究领域中，除了研究最为广泛的社区发现问题[2-3]，链路预测问题[4-6]研究如何利用网络历史拓扑信息预测未来的链路存在情况，是一项具有重要研究意义的课题.链路预测对于人们理解网络演化[7]规律至关重要，且在诸多实际应用中发挥着重要作用，如预测蛋白质间的相互作用[8]、社交网络中的朋友推荐[9]和科研网络的合作推荐[10]等.

区别于已有的链路预测研究，本文旨在研究时序网络[11]的演化机制，即给定一组由固定节点集合构成的静态网络序列，如g1,g2,…,gt,我们尝试预测该网络在未来时刻t+1到t+T的拓扑结构.一方面，传统的链路预测方法[12]多关注于静态网络的链路预测问题，忽略了每条链路上的时间戳信息，故不能被直接应用于解决时序网络的链路预测问题.另一方面，现实世界的网络系统通常具有较大的规模，包含海量有复杂联系的网络参与者.例如，一个包含105个节点和106条链路的稀疏网络，若预测未来可能生成的新链路，其搜索空间的数量级为1010；而预测未来可能消失链路的搜索空间的数量级为106，仅占前者的0.01%.受限于上述真实网络的这种稀疏性特性，有监督的链路预测方法会面临不同程度的分类样本分布失衡问题.

基于上述分析，本文构建了一个高效的链路预测框架.首先，采用ε-邻接网络序列定义时序网络的表示模型，从包含时间戳的链路集合中生成真实的网络演化序列.另外，由于生存分析中的Cox比例风险模型不需对生存时间的分布作出假定，仅通过一个模型就可分析生存时间的分布规律.因此，我们为每条链路关联一组基于拓扑相似性的特征向量，并借助Cox比例风险模型分别学习链路的消失和重连概率.然而，现实中的大多数网络为稀疏网络，即大多数的节点对之间不存在链路.因此，为压缩搜索空间，我们将节点对之间的连边情况模拟为2个玩家之间的博弈，进而提出一种基于动态博弈的双向选择机制来预测未来的网络拓扑结构.除此之外，由于计算特征向量所采用的邻近性指标是基于每个节点的邻居来计算得到的，故我们将可能与节点i发生重连的节点约束在距i的最短路径距离不超过2的范围内.此举有效地压缩了链路预测的搜索空间，提高了算法的计算效率，缓解了稀疏网络带来的分类样本分布失衡问题.

1 相关工作

传统的复杂网络链路预测方法主要分为3类：1)无监督预测方法；2)有监督预测方法；3)基于概率模型的预测方法.

无监督预测方法，也被称为评分方法[13-14].此类方法的基本假设是：若2个节点拓扑相似度越大，它们在未来形成链路的概率越高.基于此假设，无监督预测方法通过定义一系列节点对的相似性函数，来刻画网络中任一链路的存在概率.其中最常用的相似性函数包括CN(common neighbor index)[15]，JC(Jaccard coefficient)[16]，PA(preferential attach-ment index)[17]，AA(adamic-adar index)[18]等.由于这些相似性函数多采用网络的局部拓扑信息，故此类无监督预测方法通常具有较低的时间复杂度.此外，一些无监督预测方法则基于节点对连通路径特征来定义节点对的相似性函数.此类方法的基本假设是：若2个节点间的距离越短，则它们在未来形成链路的概率越高.例如，Katz[19]不仅考虑2个节点之间所有的路径，同时还利用路径的权重来计算它们之间的相似性.Lü等人[20]提出的局部路径(local path, LP)指标同时考虑直接邻居和间接邻居，获取的路径信息相对更为稳定、可靠.Yang等人[21]提出了一种基于聚类和决策树的链路预测方法.基于随机游走的链路预测算法的基本假设是：若某个节点进行随机游走，到达另外一个节点所需要的平均游走步数最少，此时2个节点的相似性最高.Lichtenwalter等人[22]在随机游走的基础上进行了一定的改进，提出了PropFlow方法.Tong等人[23]提出了一种新的随机游走方法，充分考虑网络中普遍存在的社区结构特性.Jin等人[24]提出一种基于路径反转影响和随机游走矩阵的链路预测方法.与经典的基于邻居相似度的无监督预测方法相比，基于节点对连通路径特征的无监督预测方法考虑了网络的全局拓扑特征，其预测准确率相对较高，但节点对路径特征的计算过程具有较高的时间复杂度.

有监督预测方法将链路预测问题转化为二进制分类问题，根据历史的网络演化序列构建训练样本，并借助现有的分类器，如逻辑回归[25]、支持向量机[26]、决策树[27]、多层感知器神经网络[28]和朴素贝叶斯[29]等，训练分类器参数，进而再利用训练好的分类器进行链路预测.例如，Pujari等人[30]提出一种监督式的排序融合方法对复杂网络进行链路预测.Chen等人[31]利用正则化参数来完成贝叶斯推理，进而提高学习潜在特性的辨别能力.Nguyen-Thi等人[32]提出一种基于径向基函数(radial basis function, RBF)的支持向量机(support vector machine, SVM)分类器，可有效提高预测精度且降低分类器的训练时间.基于监督学习的链路预测方法在构建训练样本时都不同程度地面临样本类别分布失衡问题.真实的网络系统呈现极强的稀疏特征，假定时刻t存在一个包含n个节点和m条链路的无向网络gt，其稀疏性表现为m≪n(n-1)2，其中n(n-1)2表示gt网络最大可能的无向链路数量.当gt演化至时刻t′，我们可以根据网络gt′与网络gt的拓扑差异，分别构建相应的训练集来预测未来的消失链路和重连链路.以重连链路预测为例，我们可以将{eij|eij∈(gt′-gt)}中的链路标记为正例样本，将{eij|eij∉(gt′-gt)}中的链路标记为负例样本.考虑到真实网络的动态演化呈现显著的渐进性，网络拓扑结构的变化是一个相对缓慢的过程.由于|{eij|eij∈(gt′-gt)}|≪|{eij|eij∉(gt′-gt)}|，采用上述方法构建的训练集中，正例样本和负例样本存在严重的分布失衡现象，传统的机器学习分类器难以训练出理想的重连链路预测模型.

基于概率模型的链路预测的基本思想是建立一个含有多个可调参数的模型，利用某种优化策略寻找参数的最优值，从而使得网络的结构和关系特征能够在模型中得到更好的体现.网络中任意节点对的重连概率可表示为基于最优参数配置的条件概率.Wang等人[33]提出了一个基于局部概率模型(local probabilistic model, LPM)的链路预测方法，可极大地降低大规模复杂网络链路预测问题的时间复杂度和空间复杂度.Coutant等人[34]提出了一种基于聚类不确定性的概率关系模型(probabilistic relational models with clustering uncertainty, PRM-CU)用于分析复杂网络的级联失效，该概率模型能够充分利用网络的拓扑信息，衡量节点对的交互能力，能够有效地提高链路预测的准确性.由于网络结构本身较为复杂，为表示更高层次的非线性网络结构，Wang等人[35]提出了结构化深层网络嵌入模型(structural deep network embedding， SDNE).与传统链路预测方法相比，SDNE模型能够有效地提取网络的局部和全局结构信息，重构网络结构，进而得到更高的预测精度.

此外，还有一些链路预测方法考虑了链路的时间戳信息和网络的社团结构特征.例如，Sharan等人[36]提出了基于不同时间关系的分类模型，采用2个实体间动态关系信息的关系模型.Rossi等人[37]提出了基于时序关系从属分类的集成预测方法.Clauset等人[38]提出了一种利用网络层次结构进行链路预测的方法，且在具有明显层次结构的网络中，该方法能取得更好的预测性能.这些链路预测方法大多对网络的拓扑结构有较高的要求，且计算时间复杂度普遍较高.

2 问题定义

现实世界的时序网络可表示为一个时序链路集γ={ip,jp,τp|p=1,2,…,M}，其中ip,jp,τp表示一个带有时间戳的时序链路，表明节点ip和节点jp在时刻τp是连通的.当忽略时序链路的时间戳和重复链路时，时序网络就退化为一个静态网络g(γ)={eij|∃ip,jp,τp∈γ}.

定义1.δ-时序范式.时刻t的δ-时序范式是一个有序链路序列Mt(δ)=its,jts,τts,…,ite,jte,τte，满足(τts≤…≤τte)∧(δ=τte-τts)，且静态网络gt(δ)=(Vt(δ),Et(δ))，Et(δ)⊆Vt(δ)×Vt(δ)是连通的.

静态网络gt演化至与其ε-邻接的网络gt′包含3种可能情况：1)从gt中消失的链路；2)gt中任意2个不连通的节点形成的链路；3)至少有1个外部节点参与形成的链路.由于外部信息具有较大的随机性，本文将重点关注前2种情况的链路预测问题，并假设出现在所有周期的节点集合是固定的.

定义3.ε-邻接网络序列.从初始网络g0(δ)=(V,E0)开始，ε-邻接网络序列由一系列耦合的静态网络组成，即Gε(g0(δ))={g1,g2,…}，满足∀t≥1：1)gt-1和gt是ε-邻接的；2)Vt⊆V，Et⊆V×V.

为强调从gt-1到gt的网络演化过程，令Mt和Rt分别表示从gt-1消失的链路集合和在gt中新生成的链路集合.显然，Mt=Et-1-Et和Rt=Et-Et-1.

定义4.多层网络[39]序列.令ε-邻接网络序列Gε(g0(δ))={E1,E2,…}中任意第t个周期的静态网络都对应一个多层网络Mt(L)={Et,Pt(L)}，其中，Et⊆V×V是周期t中静态网络的链路集，Pt(L)⊆V×V是gt最近L个静态网络投影所得的链路集：

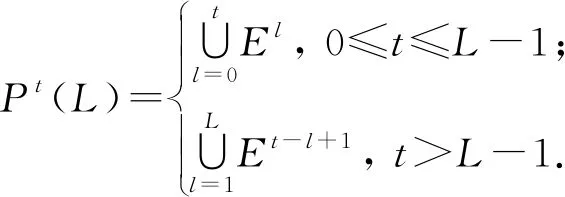
(1)

这样，由任意周期窗口L导出的多层网络序列表示为MNS(L)={M0(L),M1(L),…}.

定义5.拓扑相似性函数.令Ni={j|eij∈E*}表示节点i在某个静态网络中的邻居集合，链路ip,jp,τp的拓扑相似性可由一些相似性函数度量计算得到.例如，CN[15]，JC[16]，Sa(salton index)，So(sorensen index)，HP(hub promoted index)，HD(hub depressed index)，LN(Leicht-Newman index)，PA[17]，AA[18]等，具体为

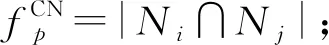
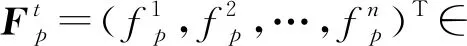
定义6.消失链路序列(missing link sequence，MLS).给定一个ε-邻接网络序列Gε(g0(δ))，由此导出的消失链路序列表示为GM(g0(δ))={M1,M2,…}，满足∀t≥1,Mt=Et-1-Et.

定义7.重连链路序列(reconnected link sequ-ence， RLS).给定一个ε-邻接网络序列Gε(g0(δ))，由此导出的重连链路序列表示为GR(g0(δ))={R1,R2,…}，满足∀t≥1,Rt=Et-Et-1.

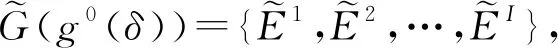
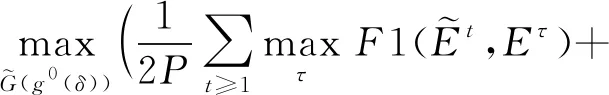
(2)

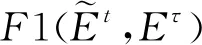
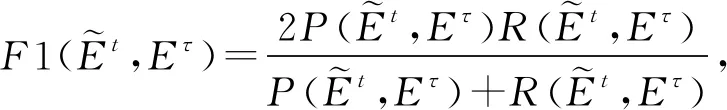
(3)

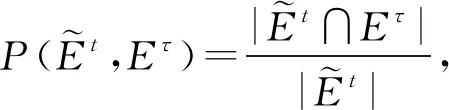
(4)

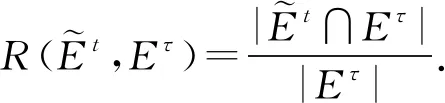
(5)

3 时序网络链路预测模型

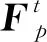
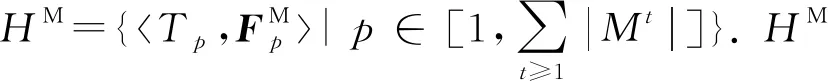
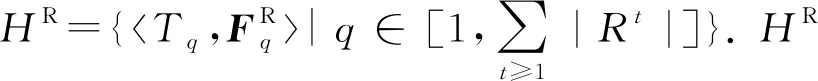
基于定义8和定义9，我们可借助于Cox比例风险模型分别学习链路消失和重连所对应特征向量的权重系数.Cox比例风险模型采用最大似然估计方法对模型参数进行估计，上述2个事件对应的协变量系数WM*和WR*可分别通过式(6)(7)学习得到：

(6)

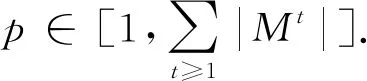
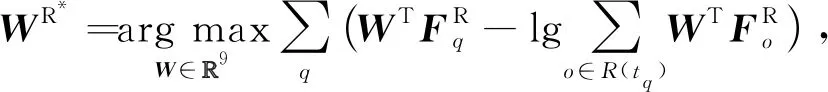
(7)

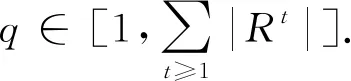
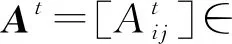
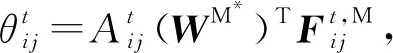
(8)

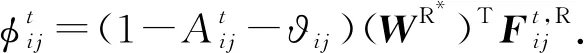
(9)

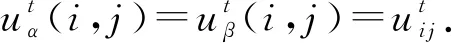
(10)

Ψt对应的纳什均衡点集为

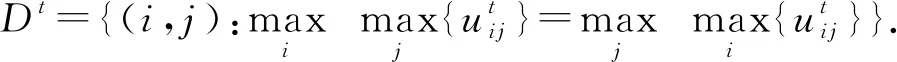
(11)

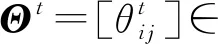
Et+1=Q(Et,Θt,Φt)=Et-Dt,M+Dt,R.

(12)

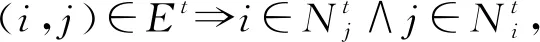
4 基于自治计算的网络演化算法

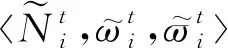
算法1.网络演化算法.

输入：初始静态网络g0(δ)=(V,E0)、时间窗口长度L、最大迭代次数I、消失链路的协变量系数WM*、重连链路的协变量系数WR*；

①t←0；

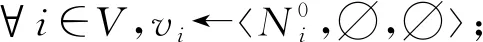
③ repeat

④ ∀i∈V，并行计算：

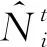
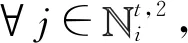
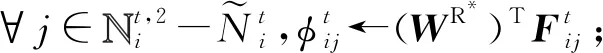
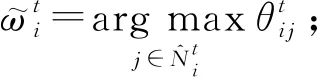
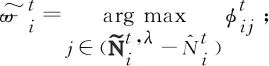
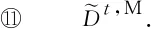
基于上述定义的自治计算系统，本文提出了基于博弈论的时序网络预测算法，具体过程见算法1.从单个节点智能体的角度来看，步骤初始化节点智能体vi的三元组为其中表示初始静态网络g0中节点i的邻居集.在每轮迭代中，步骤⑤～并行化地计算和步骤～计算相应收益矩阵Θt和Φt的纳什均衡点集；步骤生成下一周期静态网络的链路集合.当系统时间达到预设的最大迭代次数I时，算法将会输出一个预测的网络演化序列

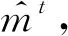
5 实验和结果

5.1 实验设置

我们选择斯坦福网络分析平台SNAP中的4个时序网络Math，Ask，Super，Stack，生成4个ε-邻接网络序列.具体来说，对于每个时序网络，我们使用第1年的数据元组构建一个无向网络，并抽取该网络的最大连通子图生成初始的静态网络g0(初始静态网络的统计特征见表1).接下来，我们进一步将ε设置为2%，生成相应的ε-邻接网络序列.图1分别记录了4个ε-邻接网络序列中相应的|Et|，|Mt|，|Rt|包含的链路数量.可见，随着时间周期t的增加，|Et|，|Mt|，|Rt|都呈显著的下降趋势.后续实验中，我们将这4个ε-邻接网络序列作为真实的网络演化序列，并将算法1分别应用于表1的4个初始静态网络.通过对比预测得到的网络演化序列和真实网络演化序列的相似度，来评价链路预测算法的优劣.

我们选择5种基于监督学习的链路预测方法，包括Logistic回归(logistic regression， LR)、SVM、决策树(C4.5)、多层感知器神经网络(multi-layer perception neural network， MPNN)和朴素贝叶斯(naïve Bayes， NB)作为对比算法.针对每个耦合的静态网络对，如(Et-1,Et)，然后将所有Mt中的链路标记为正例，并从Et-1-Mt中随机选择相同数量的链路标记为反例.这些链路实例的特征向量基于相应静态网络Et-1计算生成.这样，我们可以选择一种分类器在上述训练集上进行训练，并将训练好的分类器用于消失链路预测.采取相同的思路，我们可以构建另一个训练样本进行重连链路预测，其中节点对的特征向量基于相应的投影网络Pt-1(L)计算生成.此外，我们还选择了3种基于概率模型的链路预测方法，包括Wang等人[33]提出的LPM模型、Coutant等人[34]提出的PRM-CU模型、Wang等人[35]提出的SDNE模型.

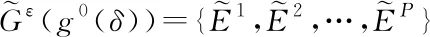
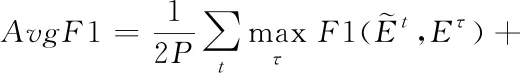
(13)

5.2 基于Cox比例风险模型的参数学习

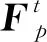
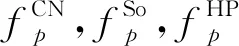
采用相同的分析过程，我们可以分别对其他3个时序网络进行类似的分析，其结果见表4.其中，每个数据集中，加粗字体的协变量系数表示该特征与对应事件是正相关，正常字体的协变量系数表示该特征与对应事件是负相关，而缺失协变量系数表示该特征与对应事件不相关.在所有数据集中，PA特征[17]与链路的消失和重连都是独立的.经典的BA网络演化模型[40]假设一个新的节点同已知网络中的节点i连接的概率同ki呈正比.而本文考虑的网络演化序列是基于固定节点集V生成的，排除了新节点加入对网络演化的影响.在这种情境下，传统的基于BA模型的无标度网络生成模型可能并不适用.

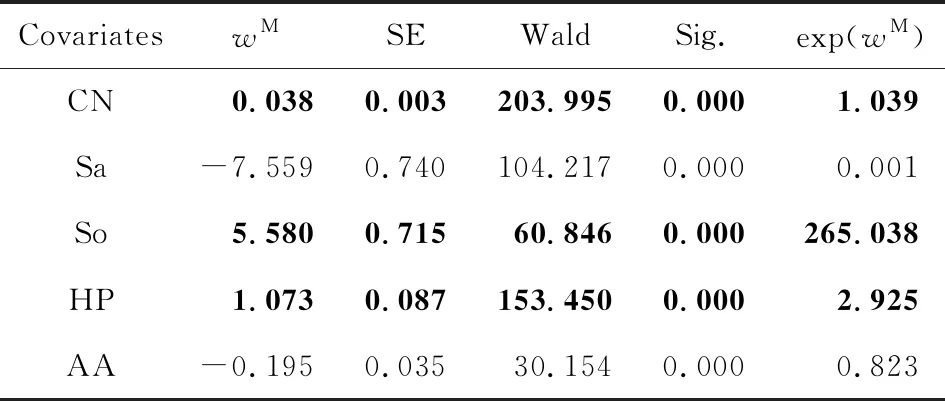
Table 2 Results of Survival Analysis on HM Dataset of theTemporal Network Math表2 基于Math时序网络HM数据集的生存分析结果

Notes: Bold values represent a positive correlation between the feature and link missing event, while the regular ones represent a negative correlation. Sig. means significance.

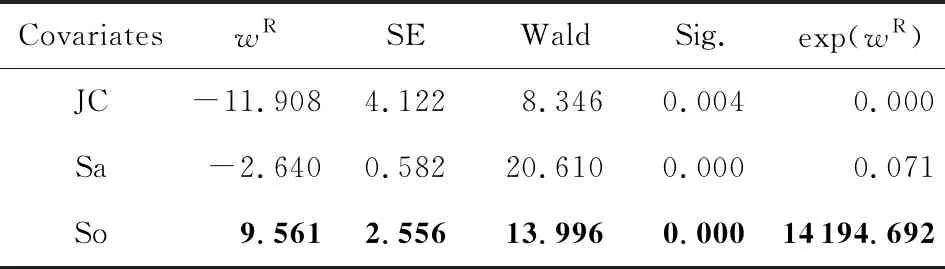
Table 3 Results of Survival Analysis on HR Dataset of theTemporal Network Math表3 基于Math时序网络HR数据集的生存分析结果

Notes: Bold values represent a positive correlation between the feature and link reconnection event, while the regular ones represent a negative correlation. Sig. means significance.

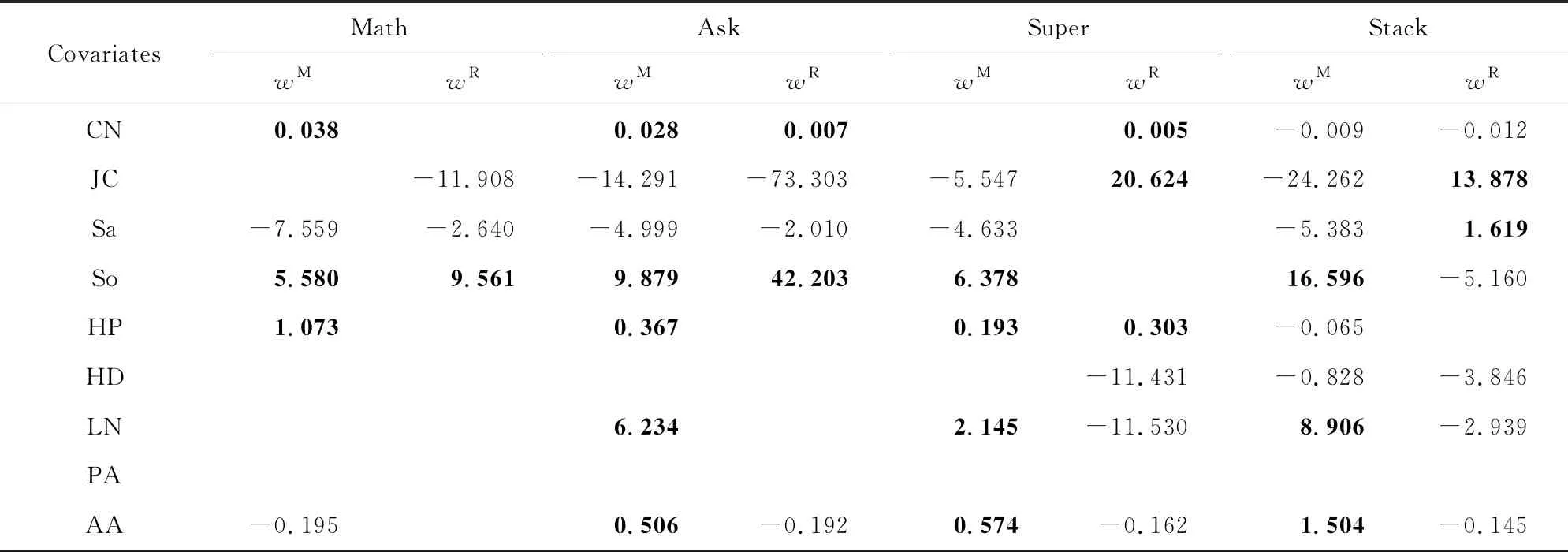
Table 4 Learning Results of the Covariate Coefficients Based on the Cox Proportional Hazards Model表4 Cox比例风险模型协变量系数学习结果

Notes: Bold values represent a positive correlation between the feature and link missing/reconnection event, the regular ones represent a negative correlation, while the missing values represent that the features are independent from the related events.

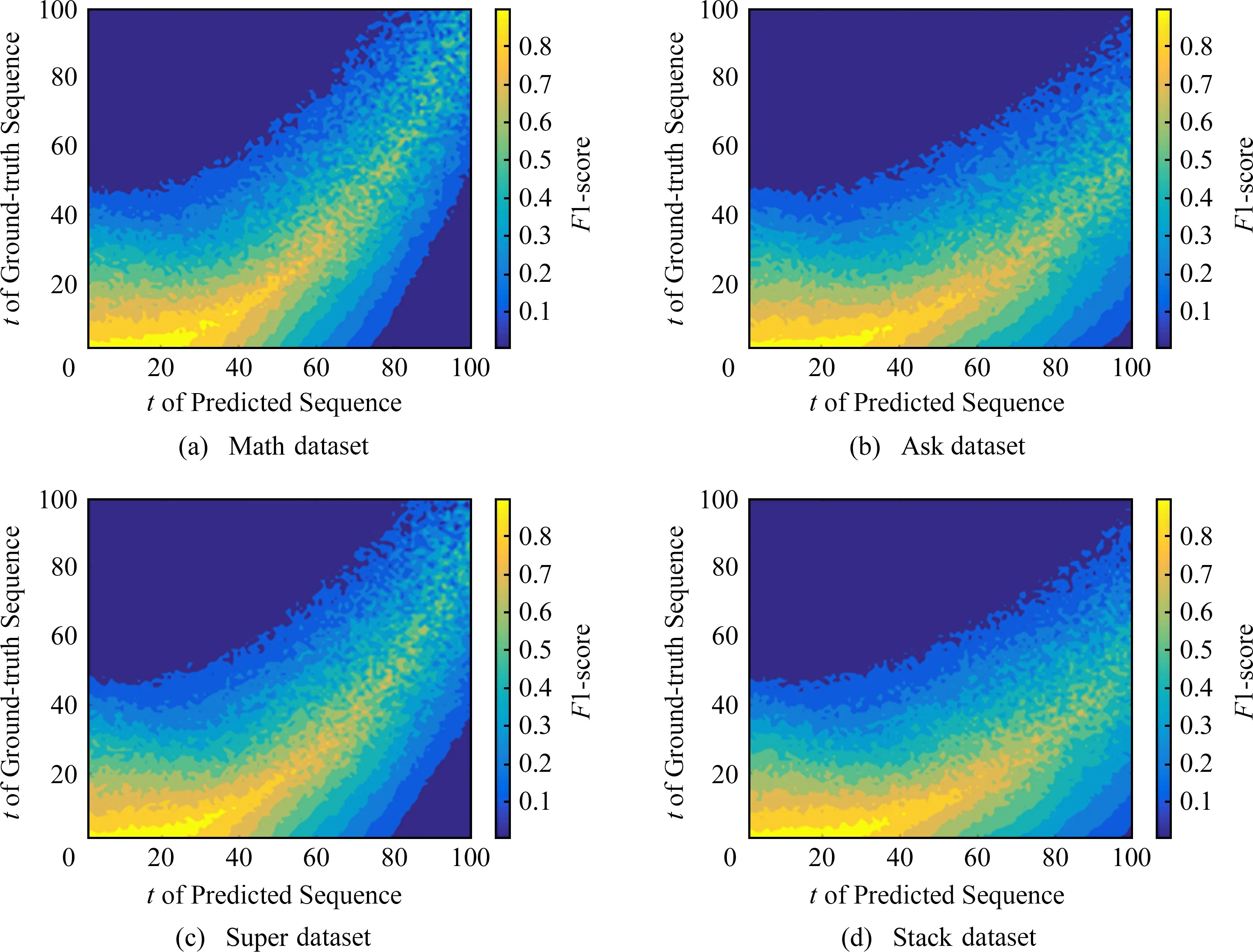
Fig. 2 The F1-score matrices between the predicted network evolution sequence and the ground-truth one图2 真实网络演化序列同预测网络演化序列的F1-score矩阵

5.3 时序网络链路预测结果

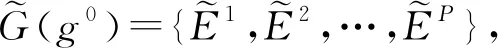
接下来，我们将算法1同其他链路预测方法进行性能对比.从图3中可观察到，本文所提方法明显优于对比算法.其中，MPNN只在Stack网络上有较好的表现，但无法准确预测其他3个网络的演化序列.多数基于监督式学习的链路预测方法对训练样本很敏感，受分类样本失衡问题的影响，这些方法尽管在消失链路预测上可以取得不错效果，但难以准确地预测重连链路.本文方法采用动态博弈的双向选择机制，可以筛选出最可能消失的链路和最可能重连的节点对.这种相对保守的预测方法尽管在召回率方面有所牺牲，但可以获得更高的准确率.因此，在AvgF1指标上，本文方法要明显优于基于有监督学习的链路预测方法.与基于概率模型的链路预测方法相比，本文方法在Super网络上的预测性能稍逊于SDNE；而在其他网络上，算法1得到的网络演化序列能更好地模拟真实网络的演化过程.

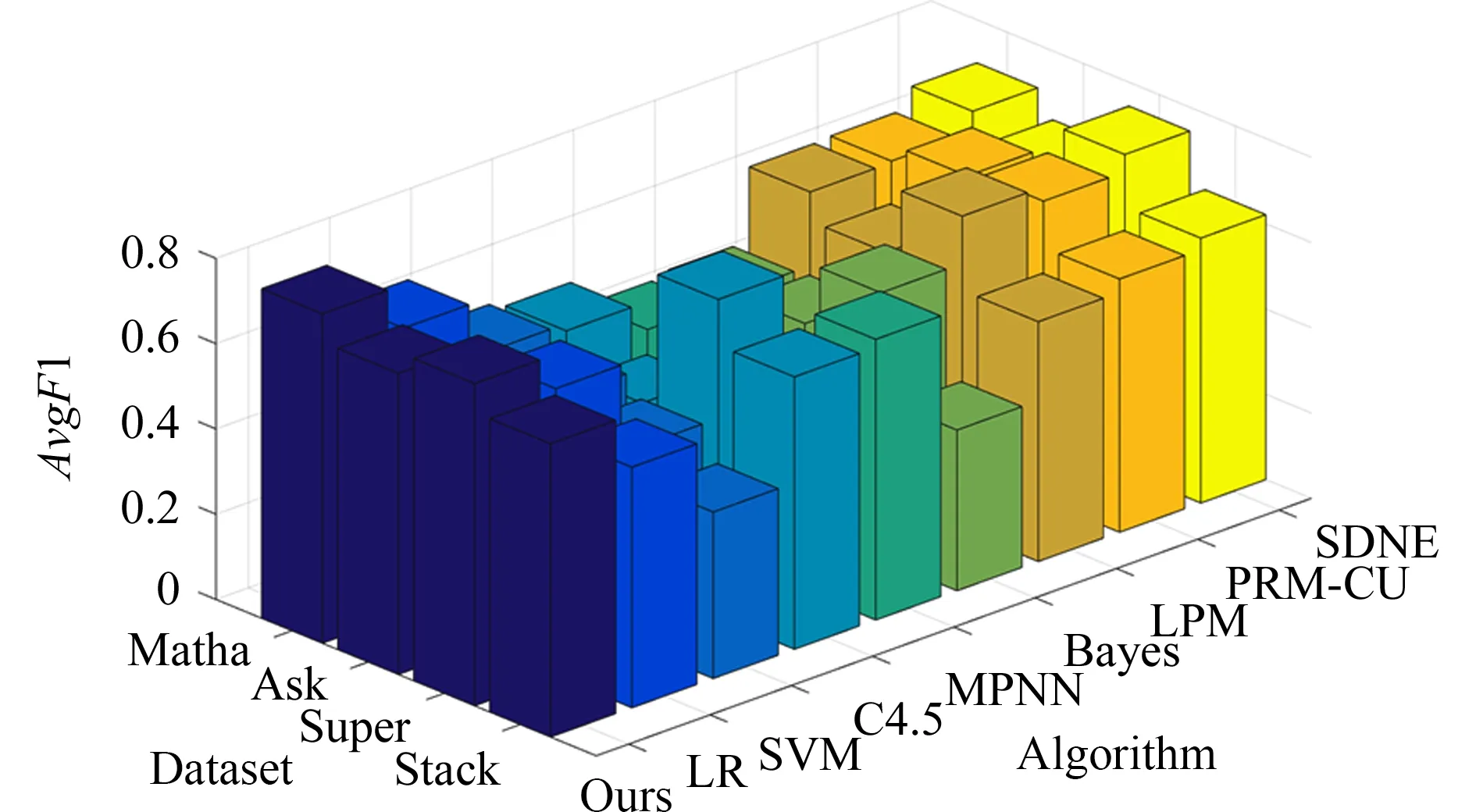
Fig. 3 Accuracy comparison of the network evolution sequences obtained by different link prediction algorithms图3 不同算法对网络演化序列的预测准确性比较

最后，我们对比了不同链路预测算法在100次连续预测过程中的执行效率，从图4可以看出，不论在小规模的Math数据集上，还是在大规模的Stack数据集上，算法1的执行效率都明显优于其他对比算法.由于本文采用了Cox比例风险模型对每个数据集中不相关的链路特征进行了排序，因此在迭代预测过程中，每个节点对的特征向量更新耗时更少.在动态博弈框架下，每个节点的特征向量更新和策略选择是独立的，故算法1可以很好地并行化.另外，我们发现本文所提方法的执行效率比基于有监督学习的链路预测算法提高了将近2倍，比基于概率模型的链路预测算法的执行效率提高了将近10倍.

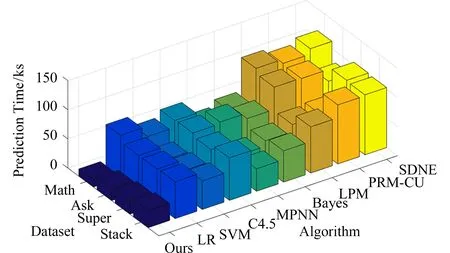
Fig. 4 Comparison of the total running time of differentlink prediction algorithms图4 不同链路预测算法的执行时间对比

6 总 结

本文提出了一种新颖的用于预测时序网络的演化序列半监督学习框架.为简化研究问题，假设时序网络的演化是在一组固定节点集中进行的，此时网络的演化预测问题转换为：如何根据历史的网络演化序列预测下一时刻静态网络的消失链路集和重连链路集.为解决此问题，首先为每条链路定义一组基于邻居相似度的特征向量，利用Cox比例风险模型学习对应链路消失和重连事件的特征向量权重.为压缩网络演化预测的搜索空间，提出了一种基于动态博弈的双向选择机制来预测未来的网络拓扑结构.在理论研究基础上，提出了一种基于多智能体自治计算的链路预测算法，并在真实时序网络数据集上验证了方法的有效性和高效性.未来将关注于如何将网络的社团结构信息融入预测模型，进而提高预测算法的准确性.