基于MODIS数据的典型草原非光合植被覆盖度估算

2019-09-12柴国奇王静璞王光镇韩柳王周龙

自然资源遥感 2019年3期

柴国奇，王静璞，王光镇，韩柳，王周龙

(鲁东大学资源与环境工程学院，烟台 264025)

0 引言

草地作为全球分布最广的植被类型之一，在陆地生态系统碳循环中起着重要作用[1]。从功能角度看，草地植被可以分为光合植被(photosynthetic vegetation，PV)和非光合植被(non-photosynthetic vegetation，NPV)2类，其中NPV主要指枯草、枯叶、枯枝、枯干和凋落物等[2]。NPV作为草原生态系统的重要组成部分，是衡量地表植被覆盖状况的重要参数[3-4]。NPV不仅能够减缓地表径流和蒸发，保持水土和营养物质，增加土壤水分渗透和有机质含量，提高土壤湿度和温度，改善土壤质量[5-7]，而且能影响生态系统的碳、水和能量的流动与循环[8]。另外，NPV在火灾风险和频率、风和水侵蚀等方面也起着关键作用[9]。因此，及时准确地掌握草原非光合植被覆盖度(fractional cover of non-photosynthetic vegetation，fNPV)信息对草地资源的合理利用以及草原生态系统的监测和保护具有重要的应用价值。

遥感技术的发展为大范围快速、准确地获取fNPV信息以及进行连续观测提供了有效的技术手段。近几十a来，国内外学者针对fNPV的遥感估算方法已开展了不少研究，并取得了一定的研究进展[2-5,10-15]。Daughtry等[5]针对NPV在2 100 nm附近波段的吸收特征构建的高光谱纤维素吸收指数(cellulose absorption index，CAI)表现较好，其与fNPV显著相关(决定系数R2=0.89)。但由于高光谱数据难以获取，无法满足大规模估算fNPV的需求[16-17]，如EO-1 Hyperion传感器已超期运行且幅宽仅有7.5 km，面临着大范围长期监测的适用性难题[18-19]。因此，研究者们开始挖掘多光谱数据对fNPV的估算潜力，如利用TM数据构建归一化差异指数(normalized difference index，NDI)[10]、归一化差异耕作指数(normalized difference tillage index，NDTI)[20]以及归一化差异衰老植被指数(normalized difference senescent vegetation index，NDSVI)[21]等来反演fNPV，然而这些指数容易受到土壤背景的影响，且不适用于草原地区PV，NPV和裸土(bare soil，BS)3种组分都存在情况下的fNPV估算[3,11]。因此Guerschman等[2]提出了基于MODIS数据B7和B6波段的比值指数(shortwave infrared ratio，SWIR32)，结合归一化植被指数(normalized difference vegetation index，NDVI)构建三元线性混合模型比较准确地估算了澳大利亚草原地区的fNPV； Cao等[11]提出基于MODIS波段的干枯燃料指数(dead fuel index，DFI)估算PV，NPV和BS这3种组分混合情况下的fNPV，结果表明DFI指数与fNPV相关性较好(R2=0.95)。但Cao等[11]的研究中混合场景覆盖度是利用端元平均光谱通过光谱混合模型模拟得到的，并不是真实的混合场景覆盖度，因此DFI指数表征野外真实混合场景fNPV的有效性有待进一步验证。

MODIS数据具备大范围、高时效、低成本等优势，已成为草地资源监测的重要数据源[1,22]。由于大多数基于MODIS数据构建的非光合植被指数(non-photosynthetic vegetation indices，NPVIs)相对较新，目前将这些指数应用于草原地区开展fNPV大范围监测的研究还较少。为此，本文选取锡林郭勒典型草原为研究区，以MCD43A4产品为数据源，比较基于MODIS数据构建的几种NPVIs指数与fNPV之间的相关关系，建立NPVIs指数反演fNPV模型并进行精度验证，以期能够找到适用于典型草原地区大范围应用的fNPV监测方法。

1 研究区概况及数据源

1.1 研究区概况

研究区位于内蒙古自治区锡林郭勒盟(E113°30′～120°00′，N43°15′～46°41′)，包含锡林浩特市、东乌珠穆沁旗、西乌珠穆沁旗和阿巴嘎旗(图1)，海拔在800～1 400 m之间。

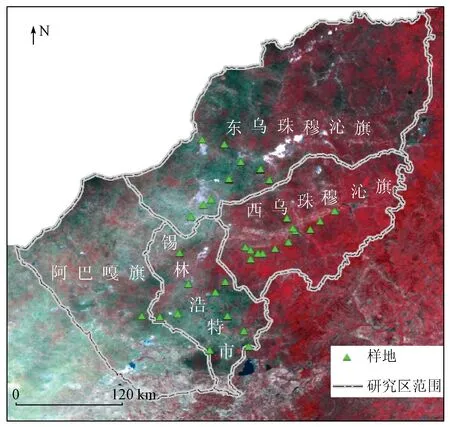
图1 研究区及实测样地位置Fig.1 Study area and sampling location

锡林郭勒草原属于中温带半干旱大陆性季风气候区，四季分明，气温偏低，年平均气温0～3 ℃，无霜期90～120 d；雨季短促，年平均降水量为295 mm，由东南向西北递减，主要集中在夏季和秋季。研究区地貌以波状高平原为主，由东南向西北方向倾斜，东、南部为大兴安岭和阴山山脉延伸余脉的交错地段；西、北部地形平坦，为高原草场；土壤以风沙土为主，部分地区有栗钙土、粽钙土；地带性植被由草甸草原向典型草原、荒漠草原过渡，植被群落中主要有羊草、大针茅、克氏针茅和蒿类(冷蒿和变蒿)等。

1.2 野外数据获取

2017年9月28日—10月3日在研究区内开展了野外地面观测实验。此时正处于植被黄枯期，采集的数据为实测样地PV，NPV和BS覆盖度数据。本次实验共获得49个样地数据(图1)，具体设置方法为：首先在研究区相对平坦均质的地区选择一个500 m×500 m大小的样地，对样地点编号并在样地中心通过手持全球定位系统(global positioning system,GPS)记录相应的地理位置信息以及样地植被情况和地貌特征；其后在每个样地内布设3～5个0.5 m×0.5 m的小样方，取所有小样方植被覆盖度的平均值作为该样地最终的植被覆盖度。与此同时，在样地中心布设一个20 m×20 m的大样方，用于与较高空间分辨率影像对应。每个0.5 m×0.5 m小样方植被覆盖度测算采用照相法[23]，利用数码相机于样方中心点正上方1.5 m处垂直拍摄2张照片，记录每个小样方对应的照片编号以及样方内植被信息。

在测算小样方植被覆盖度前，首先通过ENVI5.3软件切除照片中非样方部分。照片剩余样方部分用于进行植被覆盖度的测算，根据照片的RGB值采集PV，NPV和BS这3类地物的训练样本(阴影划分为BS类别)；然后利用监督分类中的最大似然分类法(maximum likelihood classification，MLC)对RGB照片进行分类，并结合目视解译方法判定分类结果的精度，最后根据NPV的像元数量统计出各个样方的fNPV，取2次统计结果的平均值作为该样方最终的植被覆盖度[13]。

1.3 遥感影像获取及其预处理

1.3.1 MODIS数据

MODIS数据采用经过双向反射分布函数(bidirectional reflectance distribution function，BRDF)校正处理为天顶方向观测的地表反射率(nadir BRDF adjusted reflectance，NBAR)产品数据MCD43A4(V006)，NBAR使用16 d内的数据来计算BRDF效应并对反射率数据进行归一化处理。MCD43A4(V006)提供了包括可见光、近红外和短波红外的B1—B7波段每日栅格化L3级数据产品，投影为正弦曲线投影，空间分辨率为500 m。通过LP DAAC网站(https: //lpdaac.usgs.gov)获取到研究区2017年9月30日无云覆盖的MCD43A4产品数据。

MCD43A4产品已经过几何精纠正、辐射定标和大气校正等处理，因此仅需对数据进行投影转换、图像拼接与裁剪处理即可。具体处理步骤如下：首先，利用MRT (MODIS reprojection tools)工具将下载的数据进行投影转换，将地图投影转换为WGS 84椭球的Albers Conical Equal Area投影，同时完成影像的拼接和重采样；然后，通过ENVI 5.3软件利用研究区边界矢量数据裁剪出研究区范围；最后，采用阈值法对影像中水体像元进行掩模处理[24]。

1.3.2 Landsat8 OLI数据

Landsat8 OLI数据从美国地质调查局网站下载(https: //glovis.usgs.gov)，获取时间为2017年10月5日，研究区内基本无云。由于Landsat8 OLI数据已经过几何纠正，因此只需对其进行辐射定标和大气校正即可。影像预处理主要利用ENVI 5.3软件，采用OLI传感器的辐射定标参数对原始影像进行辐射定标，然后通过FLAASH模型对影像进行大气校正，最终得到地表真实反射率。此外，为了去除水体对指数计算的影响，采用水体指数法对影像上的水体进行掩模处理。

2 研究方法

2.1 NPVIs

2.1.1 基于等效于TM的MODIS波段构建的指数

目前，常用的NPVIs大多数基于TM影像构建且多为NDI[25]，如NDI5，NDI7，NDTI和NDSVI等指数。而在可见光—近红外—短波红外波段(400～2 500 nm)范围内，MODIS的B1，B2，B3，B4，B6，B7波段分别与Landsat5 TM的B3，B4，B1，B2，B5，B7波段对应。已有研究表明，基于不同TM波段构建的NDI5，NDI7，NDTI，NDSVI及土壤耕作指数(soil tillage index，STI)同样适用于等效的MODIS波段[19]，计算公式分别为

NDI5=(B2-B6)/(B2+B6)，

(1)

NDI7=(B2-B7)/(B2+B7)，

(2)

NDTI=(B6-B7)/(B6+B7)，

(3)

NDSVI=(B6-B1)/(B6+B1)，

(4)

STI=B6/B7，

(5)

式中B1，B2，B6和B7分别为MODIS数据B1，B2，B6和B7波段的反射率。

2.1.2 基于MODIS波段构建的指数

DFI与SWIR32指数[2,11]计算公式分别为

(6)

(7)

其中，为了扩大DFI差异性，将DFI值扩大了100倍。

利用ENVI5.3软件中的band math工具根据式(1)—(7)对各个NPVIs指数进行波段组合计算。在ArcGIS10.2软件中利用地面实测样地经纬度信息提取各样地相对应的NPVIs指数值。

2.2 模型建立与验证

2.2.1 相关分析

将提取的NPVIs指数的计算值与fNPV实测值进行相关性分析，检验二者之间关系的相关程度，通过差异显著性选择相关性较好的NPVIs指数用来建立遥感估算模型。本研究利用SPSS统计软件进行相关性分析，再根据结果分析筛选最佳估算模型。

2.2.2 模型建立与验证

对49个样地的fNPV实测值从大到小排列后，按照隔二取一的模式选取建模样本(33个)与验证样本(16个)；然后采用线性回归分析方法，建立以NPVIs指数为自变量和fNPV实测值为因变量的遥感估算模型。模型验证选用R2、均方根误差(root mean square error，RMSE)和相对误差(relative error，RE)作为评价指标，R2越大、RMSE和RE越小，说明fNPV估算模型验证结果越好。其计算公式分别为

(8)

(9)

2.2.3 最优模型的稳定性验证

基于MODIS数据的fNPV估算模型稳定性验证的思路是利用线性回归方法建立较高空间分辨率的影像数据(Landsat8 OLI)和地面实测fNPV (20 m×20 m大样方)的关系，进而得到较高空间分辨率的fNPV分布结果；再以此为基础，通过ENVI5.3软件将较高空间分辨率的数据按照像元简单平均的重采样方式尺度上推到MODIS数据500 m的空间分辨率[26-27]；最后随机布设验证点，进行对比分析。另外，虽然Landsat8 OLI空间分辨率30 m略大于20 m大样方，但由于样方设置在相对均匀的区域，所以这种差别基本不会在fNPV估算中造成影响；本文选用Landsat8 OLI数据估算fNPV适用性较好的NDTIOLI指数[14]，计算公式为

(10)

式中B6OLI和B7OLI分别为Landsat8 OLI数据B6和B7波段的反射率。

3 结果与分析

3.1 NPVIs指数与fNPV的相关性

本研究对选择的7种NPVIs指数DFI，SWIR32，STI，NDTI，NDI7，NDI5，NDSVI及研究区内49个样地的fNPV实测值进行相关性分析，结果如表1所示。NPVIs指数与研究区fNPV实测值之间的相关分析中除了NDI5和NDSVI相关性相对较差之外，其余5个指数与fNPV实测值均存在着较好的相关性，相关性系数R绝对值均大于0.64，达到极显著相关水平(P<0.01)。其中DFI的相关性最好，R可达0.77； SWIR32次之，R为-0.72； NDI7相关性较低，R仅为0.64。DFI，SWIR32和NDTI与fNPV实测值的高相关性表明，利用NPVIs指数构建典型草原地区fNPV估算模型是基本可行的。

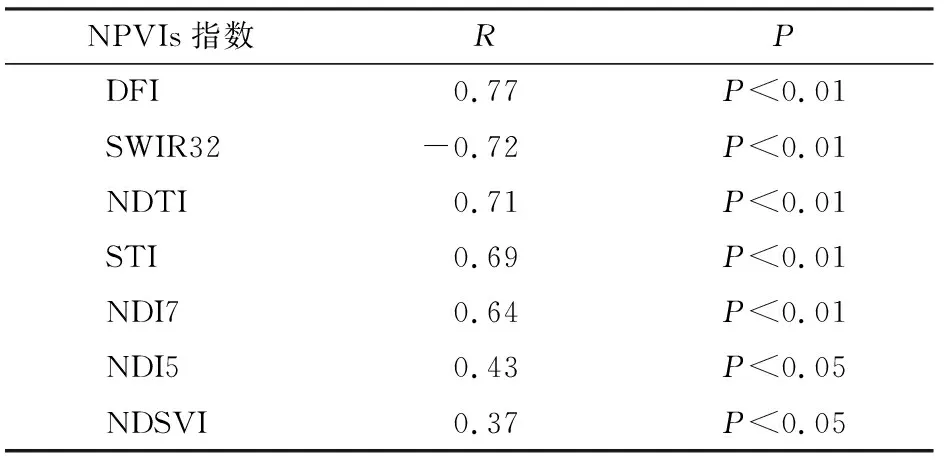
表1 NPVIs指数与fNPV实测值的相关性Tab.1 Correlation between NPVIs and fNPV

3.2 NPVIs指数构建fNPV反演模型

3.2.1 模型构建

采用线性回归分析方法，将遥感影像提取的NPVIs指数(DFI，STI，NDTI，NDI7和SWIR32)与研究区33个建模样本的fNPV实测值进行模型构建(表2)。由于NDI5和NDSVI与fNPV实测值的相关性相对较差，故在建立模型时去除。

表2 NPVIs指数与fNPV之间的反演模型Tab.2 Inversion models of non-photosyntheticvegetation index and fNPV

从表2可知，5种NPVIs指数与fNPV实测值所建立的线性回归模型均能通过极显著性相关水平(P<0.01)的F检验，R2在0.42～0.57之间。5种NPVIs中，DFI反演模型的拟合效果最好，R2为0.57；其次是SWIR32指数； STI，NDTI以及NDI7指数R2均小于0.50，且都与DFI差距较大，其中NDI7的拟合效果较不理想，R2仅为0.42。通过各NPVIs指数与fNPV实测值间的相关系数及反演模型的拟合R2可以看出，相比于其他几种指数，DFI指数反演模型的拟合效果更好，能够有效模拟fNPV的变化规律。

3.2.2 模型精度评价

利用野外同期实测样地的另外16个验证样本作为实测数据与各NPVIs指数反演模型得到的fNPV估算结果进行比较，评价不同NPVIs反演模型的估算精度，检验不同模型在典型草原地区的适用性(表3)。

从表3中可以看出，fNPV估算模型中利用DFI指数反演模型得到的估测值和实测值相关性最好，R2为0.63，RMSE与RE在5种NPVIs指数中也是最小的，RE为26.73%； SWIR32的估算效果稍次于DFI，RE为29.83%； NDTI介于SWIR32与STI之间，其RMSE与RE也均介于SWIR32与STI之间； NDI7指数的效果最差，其误差也较大，RE为34.69%。

各NPVIs指数反演模型的预测值与实测值散点图如图2所示。从图2中可以看出SWIR32，NDTI，STI及NDI7指数的反演模型高估了fNPV的低值部分，预测值位于Y=X线的上方较多，尤其是NDI7估算模型高估现象最为严重。从散点图相关方程式可知，DFI指数斜率更接近于1，且R2较大，其估算结果比较接近实测值。通过比较分析验证模型的R2和斜率，总体上看DFI指数反演模型(R2=0.63，RMSE=0.098 7，RE=26.73%)的估算效果优于其他4种NPVIs指数，fNPV预测值和实测值比较接近于Y=X线附近，这说明该模型具有较好的适用性，在典型草原地区fNPV估算方面更具优势，能够满足估算的需要。

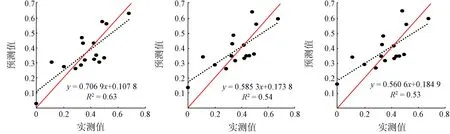
(a) DFI指数 (b) SWIR32指数 (c) NDTI指数

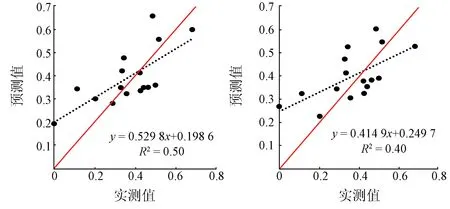
(d) STI指数 (e) NDI7指数

图2 不同fNPV估算模型预测值与实测值散点图

Fig.2ScatterplotsofdifferentfNPVestimatedmodelsbetweenpredictedvalueandmeasuredvalue

3.3 最优NPVIs指数反演fNPV模型的稳定性验证

通过获得的2017年10月5日Landsat8 OLI影像提取出NDTIOLI指数并与fNPV实测值(20 m×20 m大样方)进行回归分析，其拟合R2为0.58(P<0.01)，RMSE为0.092 9，表明该模型拟合程度较高，估算误差较小，可保证Landsat8 OLI估算fNPV的准确性。

为进一步验证最优反演模型的稳定性，采用NDTIOLI指数回归模型计算得到Landsat8 OLI(30 m空间分辨率)的fNPV并将尺度上推到500 m空间分辨率；随机布设50个验证点，将尺度一致的OLI-fNPV与DFI指数反演fNPV模型的估算结果MODIS-fNPV进行对比分析(图3)。

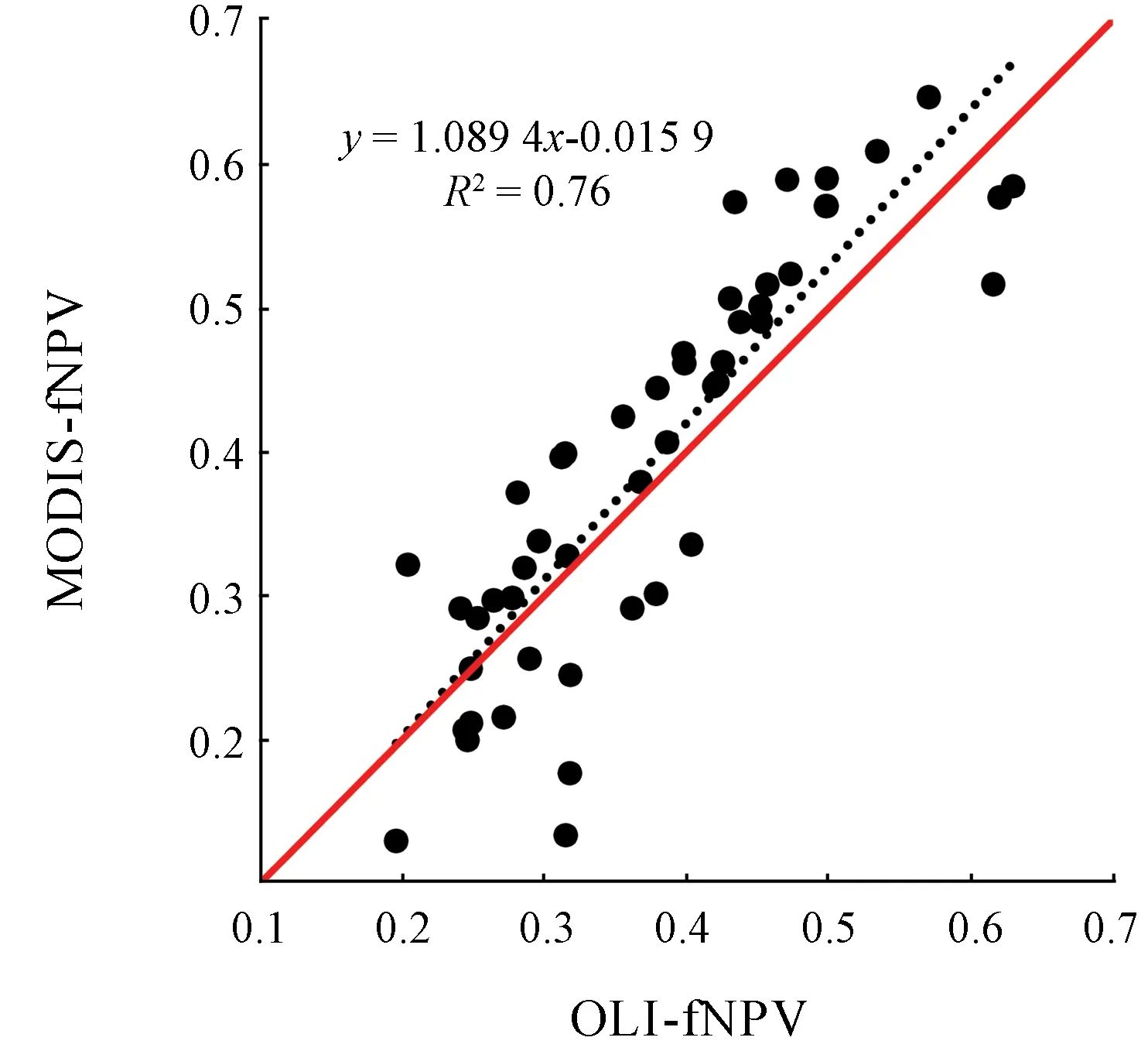
图3 研究区OLI-fNPV与MODIS-fNPV对比Fig.3 Comparison between OLI-fNPV and MODIS-fNPV

从散点图可以看出散点均匀分布在Y=X线附近，误差比较小，说明OLI-fNPV与MODIS-fNPV具有较好的一致性，进一步表明DFI指数反演fNPV模型的稳定性较好。

3.4 fNPV的空间分布特征

通过上述分析，DFI指数反演fNPV模型在研究区估算精度最高且稳定性较好。因此，利用其与fNPV间的线性回归模型进行反演，即

fNPV=0.048 7DFI-0.188 3，

(11)

式中fNPV为fNPV预测值。

该模型R2为0.57。研究区2017年9月30日的fNPV空间分布如图4所示。

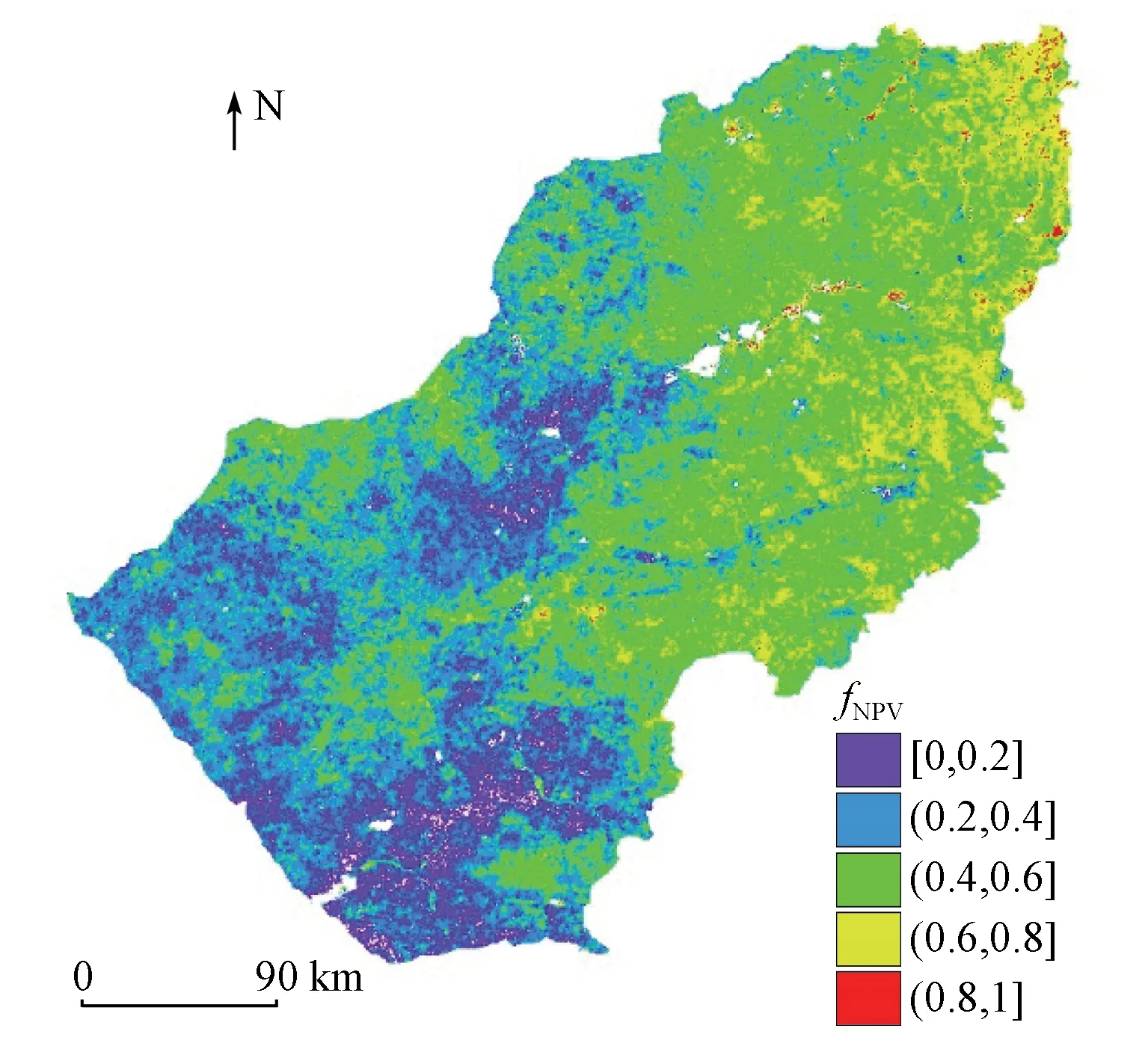
图4 研究区fNPV分布Fig.4 Distribution of fNPV in study area

从图4中可以看出9月末fNPV总体的分布特征与本次野外调查基本一致，从西南到东北fNPV值逐渐增大，整体呈现东北高西南低的趋势。分级统计典型草原地区的fNPV(表4)，主要介于(0.4，0.6]之间，像元个数大约占研究区的44.61%，这些像元主要分布在降水较多的东部；而在降水相对较少的西部，大部分地区小于0.2。

表4 2017年9月30日各个fNPV等级所占百分比Tab.4 Area percent of each fNPV grade on Sep.30,2017

4 讨论

4.1 不同NPVIs指数与fNPV间相关性差异

本研究探讨了几种由MODIS多光谱数据提取的NPVIs指数对典型草原地区fNPV的监测效果。研究表明，常用的遥感估算模型中NPVIs指数与fNPV实测值的相关性均达到显著相关水平，相关性由大到小为： DFI>SWIR32>NDTI>STI>NDI7>NDI5>NDSVI。NDI指数虽然与fNPV具有线性关系，但受BS背景的影响较大[10]； NDTI指数能够增强NPV与BS的差异，具有较好的稳定性[14,28]，但容易受到PV的影响，从而掩盖了NPV的信息[29]； SWIR32与STI同样受PV的干扰较大[19]； DFI指数的表现优于NDI，NDTI，STI，SWIR32以及NDSVI等指数，原因在于DFI相较于其他几种指数利用了更多的波段(B1，B2，B6和B7)参与运算，一定程度上减少了BS背景效应的影响，提高了估算精度；并且DFI指数是基于PV，NPV和BS这3种组分都存在的条件下建立的，能够较准确估算PV，NPV以及BS这3种组分混合情况下草原地区的fNPV[11]。

4.2 最优反演fNPV模型选择

通过线性回归分析方法对锡林郭勒典型草原地区建立了一系列NPVIs指数反演fNPV模型，其中DFI指数反演模型精度较高(R2=0.63,RMSE=0.098 7)，RE仅为26.73%。这与Cao等[30]基于MODIS09GA建立的草原地区反演模型研究结果相似，但仍存在一些差异，需要进一步研究。NDI，NDTI，STI以及SWIR32指数用于本研究区估算结果并不理想，主要原因在于这几种指数仅基于除PV以外的2种组分(NPV和BS)创建，或受BS背景影响大或受PV的干扰严重，限制了其在NPV，PV和BS这3种组分混合情况下的应用[31]。因此，选择DFI指数用于草原地区最优fNPV估算模型的构建。

DFI指数由Cao等[11]基于MODIS数据波段最先提出，用以估算PV，NPV和BS这3种组分混合情况下的fNPV，但是目前国内外利用该指数直接与MODIS影像构建经验模型估算fNPV还鲜有研究。本次研究证明了基于MODIS数据DFI指数能够有效估算典型草原地区的fNPV，并且精度较高。因此，借助于MODIS数据大范围监测、高时间分辨率的优势有必要进一步探究DFI用于fNPV时空动态变化监测的能力。

4.3 fNPV估算的复杂性和误差来源

利用遥感估算fNPV受到众多外部因素的影响，如水分吸收特征几乎能够完全掩盖NPV的光谱特征[19]。此外，不同BS类型、地表湿度和有机质含量等因素均影响NPV估算结果[25,32]。因此，遥感估算fNPV具有复杂性，需要对各种影响因素进一步分析，以更好地证明fNPV估算模型的稳定性和鲁棒性。

值得注意的是，由于野外实测数据与影像数据存在时间上不同步、样方植被覆盖度计算具有主观性的问题，这些数据误差也在一定程度上会影响估算精度。另外，本研究仅对一次实验结果进行了精度检验，样地数量相对较少且缺乏系统的地面真实性检验工作，再加上线性回归模型对实测数据的依赖性较高，模型的普适性并未得到充分的验证。因此，在后续的研究中将选取固定观测点对长时间序列的植被覆盖度情况进行连续观测，获取更多的地面实测样地数据，以更好地评价NPVIs指数估算典型草原地区fNPV的精度。