GF-4卫星影像几何定位精度分析

韩杰， 陶醉， 李慧娜， 苗宝亮， 石宏斌， 刘其悦

(1.许昌学院城乡规划与园林学院，许昌 461000； 2.中国科学院遥感与数字地球研究所，北京 100094； 3.许昌学院电气(机电)工程学院，许昌 461000； 4.中国人民解放军96608部队，洛阳 471000)

0 引言

我国高分辨率对地观测系统重大专项的建设，标志着我国民用卫星遥感技术真正跨进了“高分辨率”时代，如何从卫星数据中高精度提取地理空间信息，已经成为目前研究的热点问题之一[1-2]。作为衡量卫星影像几何质量的一个重要参数，卫星影像几何定位精度一直是科研人员和普通用户所关注的技术指标，它对卫星影像制图、地图导航和影像分类等应用服务至关重要。

高分四号(GF-4)卫星是我国高分辨率对地观测系统中的一颗静止轨道卫星，该卫星具备多种成像模式(凝视模式、跟踪模式、巡航模式、签到模式、夜间模式)，可以向用户提供极高时间分辨率(20 s重访周期)、中等空间分辨率(星下点空间分辨率50 m)和大幅宽(可见光—近红外通道/中波红外通道幅宽约500 km/400 km)卫星影像。该数据已为台风监测、环境监察和大气污染治理等研究提供了重要的数据输入[3-5]。针对静止卫星成像特点，众多研究学者已经在其影像几何定位研究领域开展了相关工作。王密等[6]针对GF-4卫星静止轨道面阵成像特点，构建了其严格成像模型，开展了几何定标工作，并检验定标前后定位精度，分析得出其定位误差可能与成像时间和成像角度有关； 徐文等[7]对GF-4卫星辐射和几何质量进行了详细评价，其中可见光—近红外影像内部畸变在沿轨和垂轨方向均优于0.8个像素，影像平面定位误差均值约为2 629.11 m，这些参数均满足了卫星研制总要求； 皮英冬等[8]提出了一种针对GF-4卫星静止轨道成像基高比较小的区域网平差方法，实现了在无控情况下，对卫星影像区域网平差的处理，并分析了平差前后影像定位误差，评价了多种像方补偿模型的优劣性； 韩杰等[9]采用仿真模拟的方法，基于GF-4卫星严格成像模型，利用GF-4卫星在轨真实数据，结合SRTM DEM数据，分析了仿真定位误差特点，探讨了仿真控制点对几何检校的影响，最后通过构建的几何检校模型，实现了该卫星高精度真实影像定位仿真模拟。

虽然上述研究已经针对静止轨道面阵成像卫星，构建了较为成熟的卫星影像几何定位精度评价体系，但是大多数研究仅是对某一时刻的卫星影像开展定位精度评价，而影像定位误差是否与某些观测因素有关，其几何检校参数是否随在轨运行时间有所变化，变化规律如何等问题都需要做进一步的研究，这对于了解该类型卫星影像几何定位误差来源，进一步优化成像模型，提高影像定位精度具有重要研究意义和实际应用价值。

相关研究结果证明Google Earth影像定位精度完全能够满足GF-4卫星影像定位精度评价要求[6,10-11]。因此，本文以GF-4卫星可见光—近红外通道影像为例，基于Google Earth影像，首先对在轨测试期间和在轨测试后影像的几何定位精度进行评价，然后分析太阳/卫星观测角及姿态角与几何定位误差之间的关系，最后探讨卫星姿态角/成像时间对相机姿态角误差补偿参数的影响。

1 几何定位精度评价

1.1 在轨测试期间定位精度评价

选取在轨测试期间(2016年3月21日)的4景GF-4卫星影像(产品号108873，108872，108864和108868)，分别在GF-4和Google Earth影像上人工选取同名点，将其坐标换算为UTM投影坐标后，比较两者物方投影坐标的差异[12]。从图1和表1中可以看出，以产品号108864和108868影像为例，影像内部几何定位误差较大，但其误差方向与误差的大小近似，属于系统误差。其中4景影像N方向平均误差约为4 591 m(约91个像素)，E方向平均误差约为20 623 m(约412个像素)，平面平均误差约为21 197 m(约423个像素)。图1中纵横坐标分别为影像行列号，箭头长度为几何定位误差大小，箭头指向为误差方向，下同。

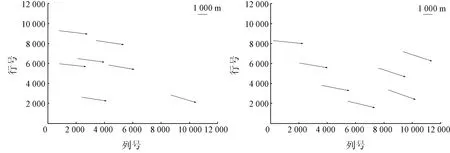
(a) 产品号108864 (b) 产品号108868

图1 在轨测试期间影像几何定位误差分布Fig.1 Error distribution of the commissioning phase period images表1 在轨测试期间的影像几何定位误差Tab.1 Geo-positional residuals of the commissioning phase period images (m)

1.2 在轨测试后定位精度评价

1.2.1 凝视成像影像定位精度分析

本研究选取了2016年11月12日北京地区GF-4卫星凝视成像影像数据(成像时间为12:05—12：32，共24景),根据云层遮盖情况，在GF-4和Google Earth影像上均匀选取6组相同的同名点对，分析几何定位精度。图2和图3分别为凝视成像影像几何定位误差分布及平均平面几何定位误差大小。从图2中可以看出，以产品号148866和148870影像为例，这2组凝视成像影像单景内部几何定位误差与在轨测试期间影像不同，其误差方向并不是朝向某一具体方向，而是大致以影像中心为原点，顺时针方向出现，产生此现象的原因需进一步分析。本文取单景影像几何定位误差绝对值作为评价指标，对凝视成像状态下影像几何定位精度及稳定性进行分析。从图3中可以看出，除个别影像外，其他影像平均平面几何定位误差大致相同。在此凝视过程中，定位稳定性较好，其中平均平面误差约为3 137 m(约62个像素)，标准差约为596 m(约11个像素)。

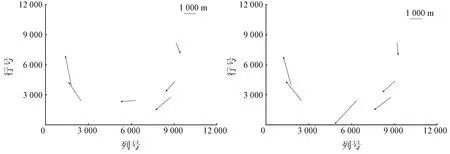
(a) 产品号148866 (b) 产品号148870

图2 凝视成像影像几何定位误差分布

Fig.2Errordistributionofthestaringimagingimages

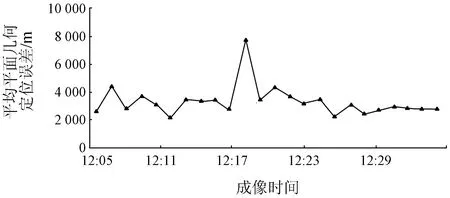
图3 凝视成像影像平均平面几何定位误差Fig.3 Average geo-positional errors inplane of the staring imaging images

1.2.2 长时间序列影像定位精度分析

以北京地区为研究区域，收集在轨测试后该区域长时间序列影像(成像时间为2016年6月18日—2016年11月15日，共32景)，根据每景影像云层分布特点，在GF-4和Google Earth影像上均匀选取同名点对，进行定位精度分析。从图4中可以看出，以产品号124308和124978影像为例，单景影像内部几何定位误差出现按照顺时针排列和方向一致这2种现象。同样统计单景影像内部平均平面几何定位误差后，对长时间序列影像几何定位精度进行分析(图5)。从图5中可以看出，影像几何定位误差波动较为明显，且部分影像误差较大，平均平面误差约为5 335 m(约106个像素)，标准差约为4 675 m(约93个像素)。因此，若要利用该卫星影像进行长时间序列定量遥感研究，则需更加注意影像间的几何定位问题。

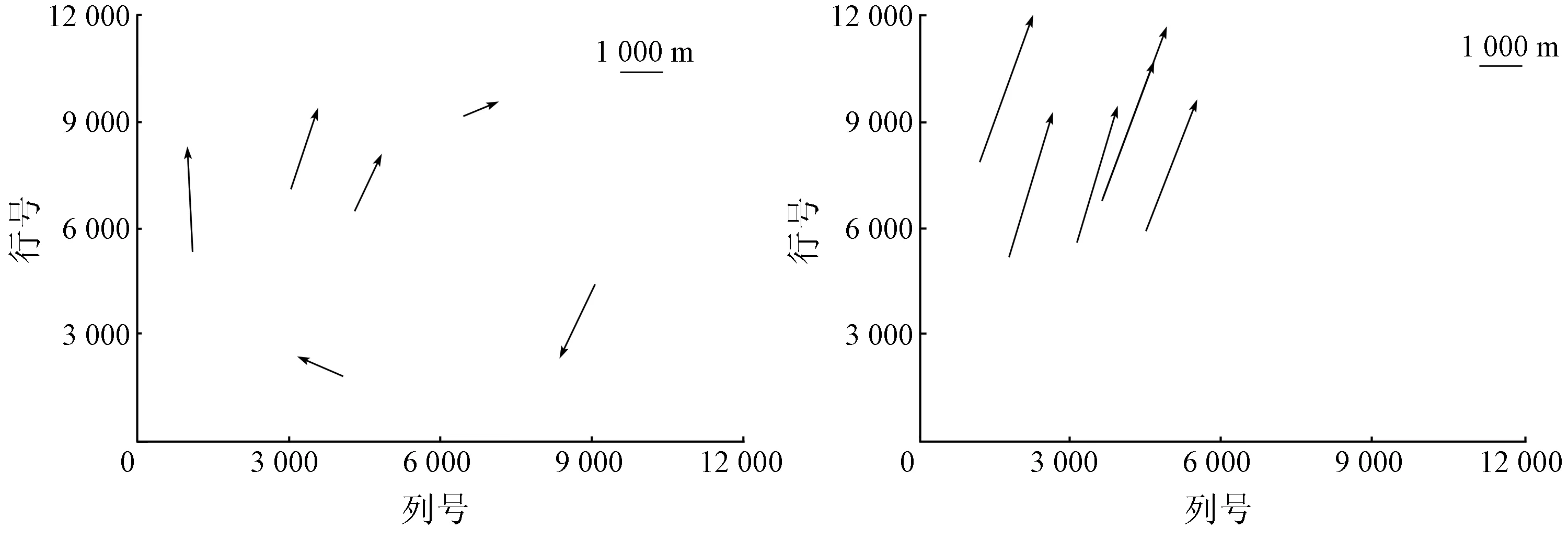
(a) 产品号124308 (b) 产品号124978

图4 长时间序列影像几何定位误差分布

Fig.4Errordistributionofthelongtimesequenceimages

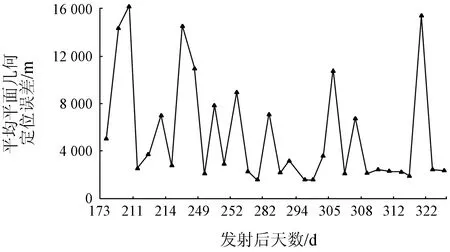
图5 长时间序列影像平均平面几何定位误差Fig.5 Average geo-positional errors in planeof the long time sequence images

2 几何定位精度影响因素分析

2.1 几何定位精度与太阳/卫星观测角度的关系

以北京地区长时间序列影像集为例，分析影像几何定位误差与太阳/卫星观测角度之间的关系(图6)，其中太阳/卫星观测角度可以从影像XML文件中提取。从图6可以看出，影像平均平面几何定位误差与太阳高度角/方位角和卫星方位角/天顶角之间并不存在十分明显的相关关系。

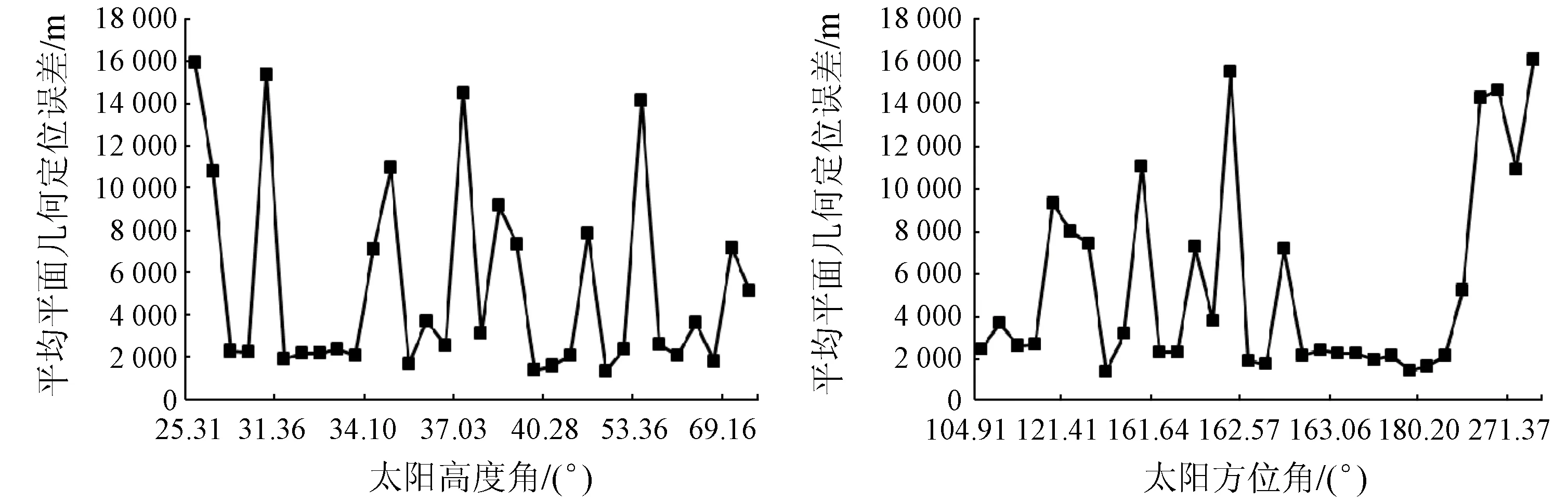
(a) 与太阳高度角之间的关系 (b) 与太阳方位角之间的关系

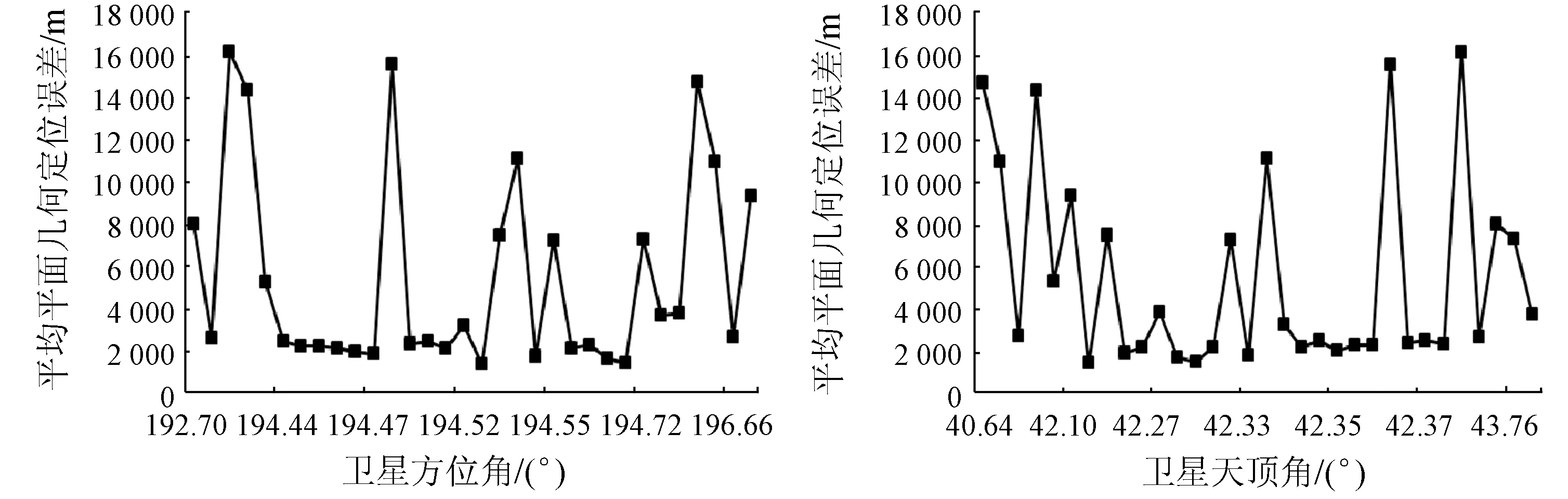
(c) 与卫星方位角之间的关系 (d) 与卫星天顶角之间的关系

图6 几何定位误差与太阳/卫星观测角度的关系

Fig.6Relationshipsbetweenthegeo-positionalerrorsandtheobservationangleofthesatelliteandsun

2.2 几何定位精度与卫星姿态角的关系

由于GF-4卫星位于赤道上空，其偏航角变化很小，因此本文仅分析影像定位精度与卫星滚动角和俯仰角之间的关系。选取2017年1月25日，青海—云南地区3景影像(产品号154607，154608和154621)用于分析卫星滚动角与几何定位误差之间的关系； 选取2017年7月11日，宁夏—渤海地区的5景影像(产品号168000，168001，168002，168003和168004)，用于分析卫星俯仰角与几何定位误差之间的关系，其中卫星姿态角信息可从影像XML文件中提取。从图7中可以看出，随着卫星滚动角减小/俯仰角增加，其几何定位误差逐步降低。

(a) 与卫星滚动角之间的关系 (b) 与卫星俯仰角之间的关系

图7 影像平均平面几何定位误差与卫星姿态角的关系

Fig.7Relationshipsbetweenthegeo-positionalerrorsandthesatelliteattitudeangles

2.3 卫星姿态角/成像时间与相机姿态角误差补偿参数的关系

以往研究结果表明，受卫星发射及发射后外界环境的影响，实验室测量得到的相机安装角度会发生变化，使其不能直接用于高精度影像定位[12-13]。因此通常利用地面控制点对在轨运行期间相机姿态角进行检校，获取其补偿参数后，对严格成像模型进行优化，提高影像直接定位精度。本文采用仿真模拟的方式，获取相机姿态角误差补偿参数。首先，将利用影像有理函数模型(rational function model，RFM)获得的定位信息作为“真实值”[14]； 然后，基于GF-4卫星多光谱相机严格几何模型，结合在轨真实影像卫星姿态角参数(可从XML文件中提取)，将获得的定位信息作为“测量值”[15]； 最后，根据相机外检校模型，获取相机姿态角误差补偿参数，进而分析卫星姿态角/成像时间与相机姿态角补偿参数之间的关系[6-7]。选取2017年11月24日中国西部地区的5景影像(产品号180416，180425， 180426，180435和180436)分析滚动角的影响，选取2017年7月11日宁夏—渤海地区的5景影像(产品号168000，168001，168002，168003和168004)分析俯仰角的影响，选取北京地区长时间序列影像分析成像时间(按天和按小时)的影响，结果如图8—11所示。

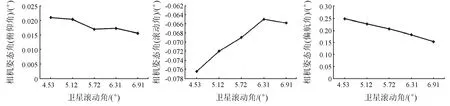
(a) 与相机姿态角(俯仰角)的关系(b) 与相机姿态角(滚动角)的关系(c) 与相机姿态角(偏航角)的关系

图8 卫星滚动角与相机姿态角误差补偿参数的关系

Fig.8Relationshipsbetweenthesatelliterollangleandthecompensationparametersofthecameraattitudeconstantangles

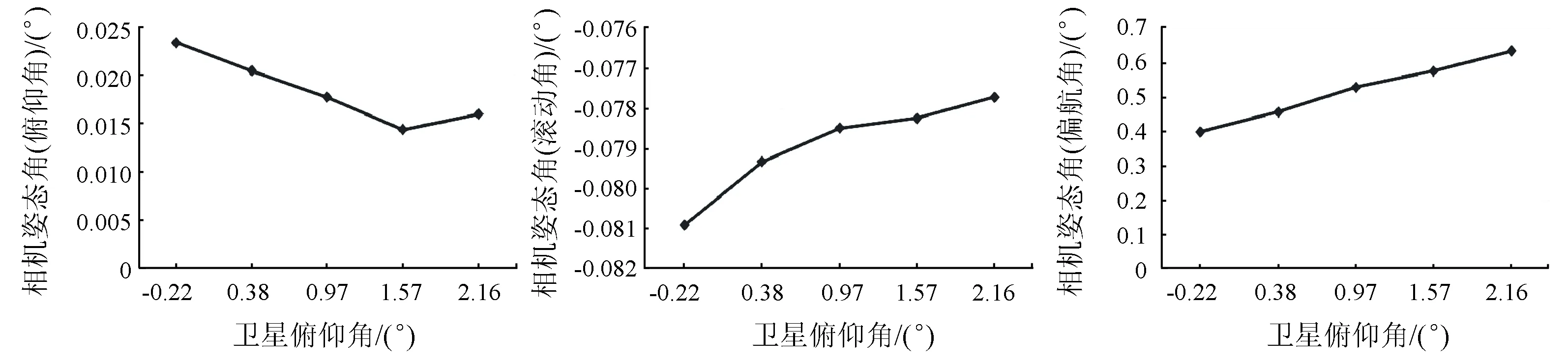
(a) 与相机姿态角(俯仰角)的关系(b) 与相机姿态角(滚动角)的关系(c) 与相机姿态角(偏航角)的关系

图9 卫星俯仰角与相机姿态角误差补偿参数的关系

Fig.9Relationshipsbetweenthesatellitepitchangleandthecompensationparametersofthecameraattitudeconstantangles

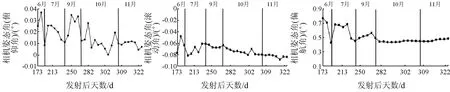
(a) 与相机姿态角(俯仰角)的关系(b) 与相机姿态角(滚动角)的关系(c) 与相机姿态角(偏航角)的关系

图10 卫星成像时间(按天)与相机姿态角误差补偿参数的关系

Fig.10Relationshipsbetweentheimagingtimebydayandthecompensationparametersofthecameraattitudeconstantangles

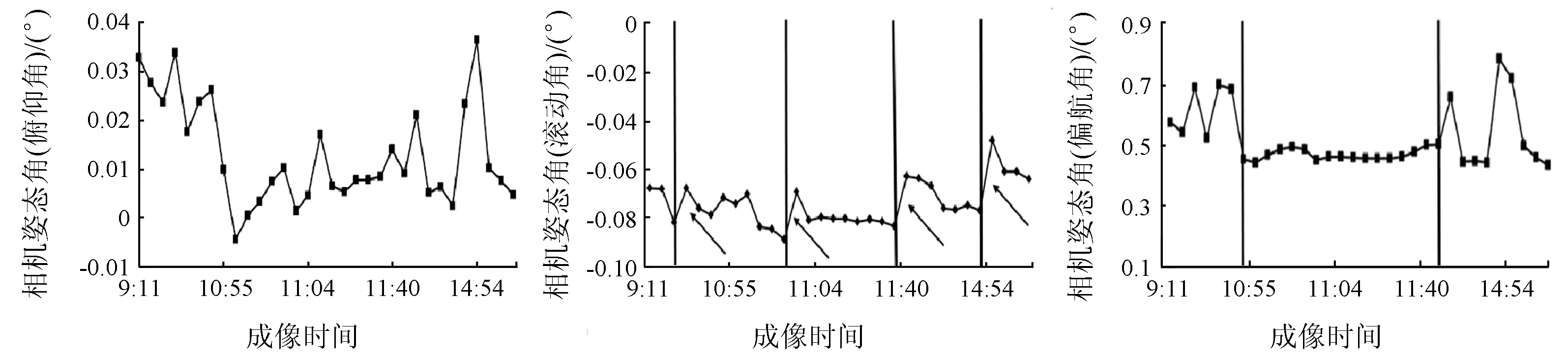
(a) 与相机姿态角(俯仰角)的关系(b) 与相机姿态角(滚动角)的关系(c) 与相机姿态角(偏航角)的关系

图11 卫星成像时间(按小时)与相机姿态角误差补偿参数的关系

Fig.11Relationshipsbetweentheimagingtimebyhourandthecompensationparametersofthecameraattitudeconstantangles

从图8可以看出，随着卫星滚动角的增大，相机姿态角误差补偿参数的绝对值逐渐变小。从图9可以看出，随着卫星俯仰角的增大，相机姿态角(俯仰角和滚动角)的绝对值逐渐变小，而相机姿态角(偏航角)逐渐变大。从图10可以看出，相机姿态角(滚动角和偏航角)相对于相机姿态角(俯仰角)而言更加稳定一些，虽然前两者在9月份之前有所波动，但9月份以后变化幅度很小。另外，通过相机姿态角(俯仰角)与成像时间(按天)的关系可以看出，6，7，9，11月份，该角度均出现了“波峰”的现象，而在10月份出现了“波谷”的现象。从图11可以看出，相机姿态角(俯仰角)与成像时间(按小时)之间出现“波谷”现象，即先变小后增大； 对于相机姿态角(滚动角)而言，整体上比较稳定，但是可以发现，该补偿角在某些时间点处，出现明显的增加现象； 对于相机姿态角(偏航角)而言，在10：20—11：40之间非常稳定，而在其他时间有所波动。由于缺少零级数据支持，出现上述现象的具体原因需进一步分析。

3 结论

1)针对GF-4高轨静止面阵相机特点，综合评价了在轨测试前后及不同成像模式下(凝视成像和长时间序列成像)，影像几何定位误差。

2)利用在轨真实数据，分析了太阳观测角、卫星观测角/姿态角与几何定位误差之间的关系，探讨了卫星姿态角/成像时间与相机姿态角误差补偿参数之间的关系。

3)由于缺乏零级及相关辅助数据，本文只展示了在对几何定位精度分析中出现的现象，而出现该现象的具体原因，则需进一步分析。

志谢：感谢中国资源卫星应用中心为本文研究提供GF-4卫星影像数据，感谢Google Earth为本文提供参考信息。