城区复杂下垫面天空视域因子参数化方法——以北京鸟巢周边地区为例

段欣， 胡德勇， 曹诗颂， 于琛， 张亚妮

(1.首都师范大学资源环境与旅游学院，北京 100048； 2.资源环境与地理信息系统北京市重点实验室，北京 100048)

0 引言

近几十a来，随着我国经济的快速发展和城市人口的急剧增加，城镇化进程持续加快。城市形态对城市微气候具有重要影响，许多研究试图揭示城市形态与热环境之间的关系[1]。天空视域因子(sky view factor,SVF)是最受关注的城市形态参数之一，常用于描述城市三维几何结构，它的定义为： 夜晚从城市地面发出的长波辐射，一部分被树木、建筑物等障碍物阻挡并吸收，另外一部分则被射向天空，这部分被释放的辐射与总的辐射比被称为SVF，它是一个没有量纲且介于0～1之间的值[2-3]。SVF广泛应用于城市热岛效应[4]、城市能量平衡[5-6]和城市表面温度[7-8]等方面的研究。大量研究显示，热岛效应与SVF呈负相关关系[2，9-11]； 地表温度也受SVF的影响[12-13]。因此，精确提取城区复杂下垫面的SVF具有重要意义。

目前，国内外的研究者提出了许多不同的计算SVF的方法。 Steyn[14]在1980年引入了鱼眼相片计算SVF，他提出人为地将鱼眼相片分割为圆环进行计算，但这既耗费时间也耗费人力。而后研究者提出了各种其他利用鱼眼相片计算的方法，其中包括： 借助计算机程序对周围环境进行手动追踪，然后自动计算SVF[15-16]； 通过软件自动追踪周围环境[17]来获取SVF； 通过数码相机进行增强，可以在特定位置快速估算SVF等。到目前为止，利用鱼眼相片直接计算SVF仍然是最佳的方法，但是由于鱼眼相片不能大范围获取，所以该方法无法适用于大范围的SVF计算。2001年Grimmond等[18]使用LI-COR LAI-2000植物冠层分析仪，提出利用鱼眼光学传感器测量自动漫射非截距光获取SVF，该方法的数据收集与处理速度快，但是对天气条件有一定的要求，并且对于操作系统的要求较高； Chapman等[19]提出使用简单且便宜的全球定位系统(global positioning system,GPS)接收机来获取卫星可见性数据，然后将其用于获取与SVF相关的位置指标，进而估算SVF,该方法适用于城市环境中的SVF的估算，但准确度较低,此外，每个GPS单元的性能也会有所不同，从而不可能制定通用方程式; Hodul等[20]在2016年提出利用阴影监测的方法从Landsat数据中提取SVF，该方法的缺陷是许多由灌木或草地投下的小阴影可能会导致SVF偏低; Ratti等[21]提出利用3D建筑数据库计算得到SVF，这种SVF模型已经得到验证，并且结果精确度较高[22-23]； Souza等[24]通过对ArcView R进行扩展来计算SVF，但ArcView R的学习难度较高，并且难以实现诸如多表面反射和复杂树木建模等城市特征； Matzarakis等[25]在2011年提出同时使用栅格和矢量数据来计算SVF，该方法的缺点是虽然可以从ASCII数据中读取栅格数据，但必须通过Rayman中的专用编辑器手动输入矢量数据； 德国汉堡大学的Zakšek等[26]2011年将SVF应用于山地的地形可视化，提出利用数字高程模型(digital elevation model,DEM)数据，快速提取斯洛文尼亚西南部的岩溶地区与Tonovcov grad考古遗址的SVF，进而对地形进行可视化表达，但该研究仅限于研究山区或者特定区域如岩溶区域的地形可视化，并未涉及下垫面环境复杂的城市地区的SVF提取。

综上所述，目前研究快速获取城市地区大范围复杂下垫面的SVF还存在一定的困难。本文基于Zakšek等[26]提出的利用DEM数据进行山地可视化的方法，以北京市鸟巢周边地区为例，利用数字表面模型(digital surface model,DSM)数据快速获取城市区域连续的SVF； 同时以鱼眼相片采样提取的SVF作为验证数据，探讨通过DSM数据大范围提取城市复杂下垫面SVF方法的适用性。

1 研究区概况与数据源

1.1 研究区概况

研究区位置及DSM数据如图1所示。

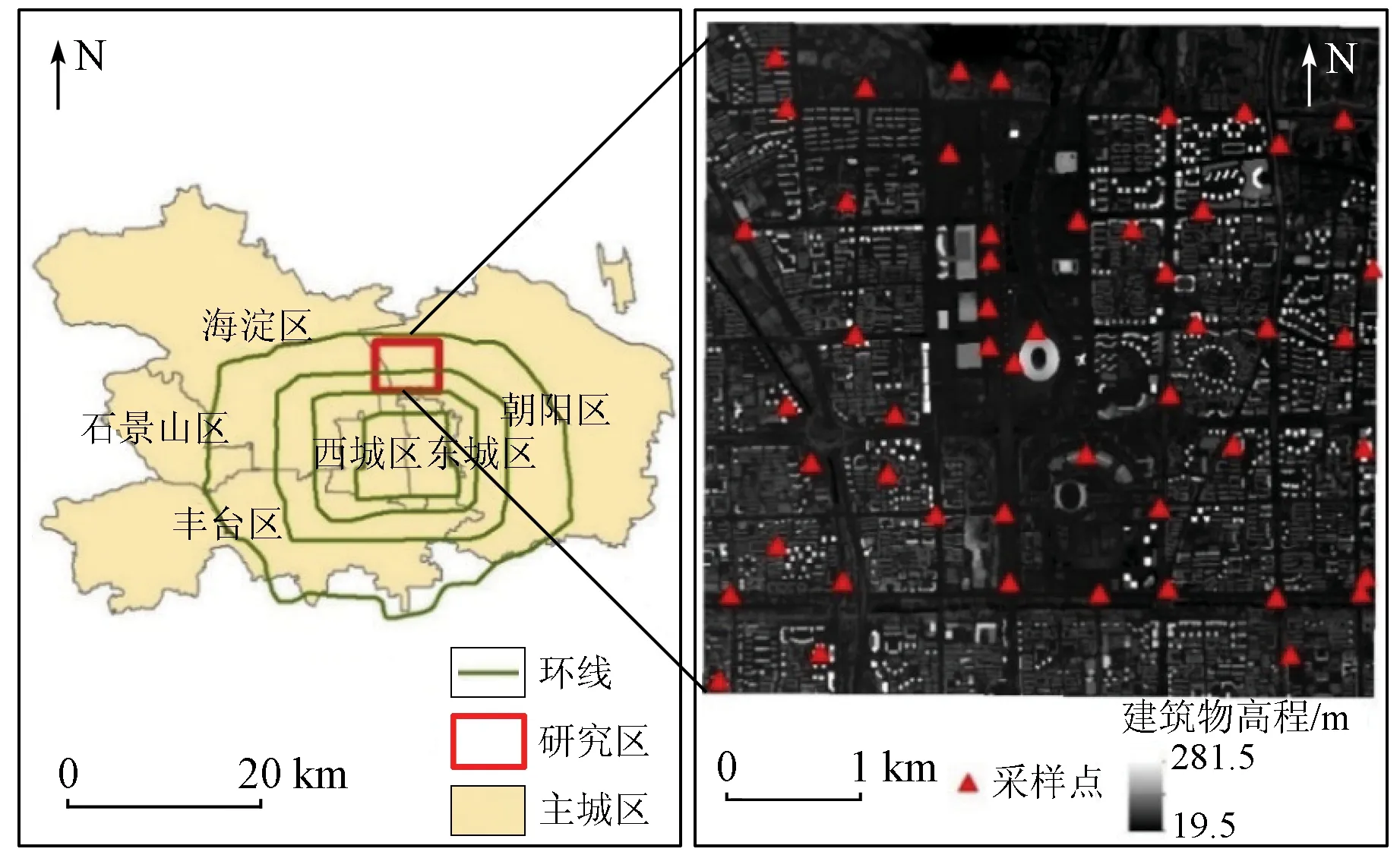
(a) 研究区地理位置示意图(b) 研究区机载LiDAR DSM

图1 研究区概况

Fig.1Overviewofthestudyarea

研究区位于北京市鸟巢(国家体育场)周边，在以其为中心的长、宽约5 km的范围内。地处中纬度地区，海拔在21～55 m之间，平均高程为34 m。区内地物有植被、水体、裸地和建筑物等，下垫面环境较复杂，建筑物高度、密度和形态多样，既有北辰集团等建筑物密度高、形态多样的区域，也有奥林匹克公园等低建筑物密度区，适合鱼眼相片数据的采样收集。

1.2 数据源及其预处理

研究搜集了覆盖北京市鸟巢周边地区的机载LiDAR数据，该数据是通过搭载于Yun-5飞机上的Leica ALS 60系统于2016年5月20日收集的，其空间范围见图1(b)区域。数据空间分辨率为0.5 m，投影方式为UTM，坐标系为WGS-84 UTM-50N，点云密度大约为2～4 点/m2。对点云数据先进行预处理，然后进行分割、滤波和分类，再将获得的地面点按照一定的内插方法生成0.5 m空间分辨率的DSM数据。生成的DSM与50个地面控制点x,y,z坐标对比，水平误差小于1个像元(0.5 m)，高度误差小于0.15 m。

本研究选取平均分布于研究区范围内的48个采样点，如图1(b)所示。为保证数据收集的准确性，使相机能够充分收集地面的数据，在实际采样时将相机放置于冠层底部，垂直地面朝向天空。相机采用尼康D610全幅相机，该相机有效像素为2 426万，最高图像分辨率可达6 016×4 016，镜头为适马(SIGMA)8 mm F3.5 EX DG FISHEYE 定焦鱼眼镜头，该镜头焦距范围为8 mm，具有135 mm全画幅镜头，视角范围可达180°。由于下垫面情况复杂，为了全面收集采样点的SVF数据，在不同建筑物密度、建筑物形态的区域都进行了采集。图2为部分采样点的鱼眼相片示例。

(a) 操场(b) 居民区

图2 采样点鱼眼相片示例

Fig.2Fisheyephotosatsamplingpoints

2 研究方法

2.1 利用DSM获取城市下垫面SVF

利用DSM获取SVF是通过引入立体角来计算的。如果在DSM上选取一个观测点，那么立体角定义为： 以观测点为球心，构造一个单位球面，任意物体投影到该单位球面上的投影面积，即为该物体相对于该观测点的立体角。立体角是单位球面上的一块面积，这和“平面角是单位圆上的一段弧长”类似。建筑物立体角示意图如图3所示。

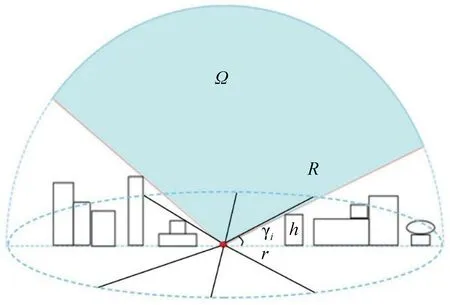
图3 立体角示意图Fig.3 Schematic diagram of solid angle

建筑物立体角Ω(图3)的计算公式为

(1)

式中：γ为建筑物高度角;λ为建筑物方位角;s为半球曲面。假定在短距离(10 km范围内)的距离上地球曲率的影响可以忽略不计，根据定义，整个半球的立体角为

(2)

式中：φ为建筑物在半球中的水平角;γ为建筑物在半球中的高度角。假设在水平面以上，可见天空受到地物的限制，观测点在所有方向上的建筑物都具有相同的高度角，则立体角为

(3)

式中：γ为建筑物的高度角。由于实际观测点在各个方向的建筑物不同，因此建筑物高度角也不相同。将半球以观测点为中心，在水平方向分成若干个大小相等的区域，生成不同的搜索方向。在不同搜索方向上，以观测点为搜索中心，搜索半径为R，从垂直天空方向向水平方向搜索，直到遇到建筑物为止(如图3所示)。式(3)中的立体角可以通过在选定的搜索方向的建筑物高度角来有效地计算，计算公式为

(4)

式中：n为搜索方向的数量;γi为不同建筑物的高度角。其中，γi由建筑物与观测点的水平距离r和建筑物最高点与地平线之间的高度差h所决定，当搜索半径R取不同值时，r与h也发生变化，所以γi受R大小的影响。因此得到观测点的SVF的计算公式为

(5)

SVF受搜索方向的数量n及不同建筑物的高度角γi的影响。由于γi受搜索半径大小的影响，因此影响SVF大小的最主要因素是搜索方向与搜索半径[26]。为寻找反演城区复杂下垫面的SVF的最适宜尺度，本研究分别选择20，30，50，65，80和100个像元大小的搜索半径； 搜索方向数量选择为8，16与32个，进行SVF的计算。

2.2 利用鱼眼相片计算城市下垫面SVF

Holmer[15]提出基于像素法提取SVF。该方法利用拍摄观测点的鱼眼相片计算该点的SVF。由于鱼眼相片中使用行和列的二次像素，所以首先需要通过在相片上的3个点(cj，dj)(j=1,2,3)的位置来确定鱼眼相片的圆心与半径，计算公式为

r2=(cj-c0)2+(dj-d0)2，

(6)

式中： (c0，d0)为圆心坐标；r为圆的半径。考虑不同建筑物投影在平面上的大小取决于与天顶角的距离，不同位置的像元权重不同，接下来需要确定天空视图权重图像。将整个圆分解为r个圆环，每个像素的权重可以表示为

(7)

式中： (c,d)为像素在图像上的坐标；k=1,2,…r。为划定鱼眼相片范围，鱼眼相片圈以外的区域需要掩盖。鱼眼相机拍摄的是彩色图像，每个像素具有以24位编码表示的RGB值： 3个分别用于红色、绿色和蓝色的8位编码，取值为0～255。将这些编码转换为8位编码，取值为0～215。每个像元的像元值表示为

V=B+6G+36R，

(8)

式中B，G，R分别为该像元蓝色、绿色、红色的编码。通过研究像素值的频率分布以及人工选择阈值来将图像划分为天空部分与非天空部分(即有物体遮挡的部分)。在得到的结果图像中，将天空部分的像元赋值为1，非天空部分的像元赋值为0。最后将得到的划分结果图像与天空视图权重图像相乘，所有像元乘积之和为SVF。

2.3 总体技术路线

本文技术路线如图4所示。

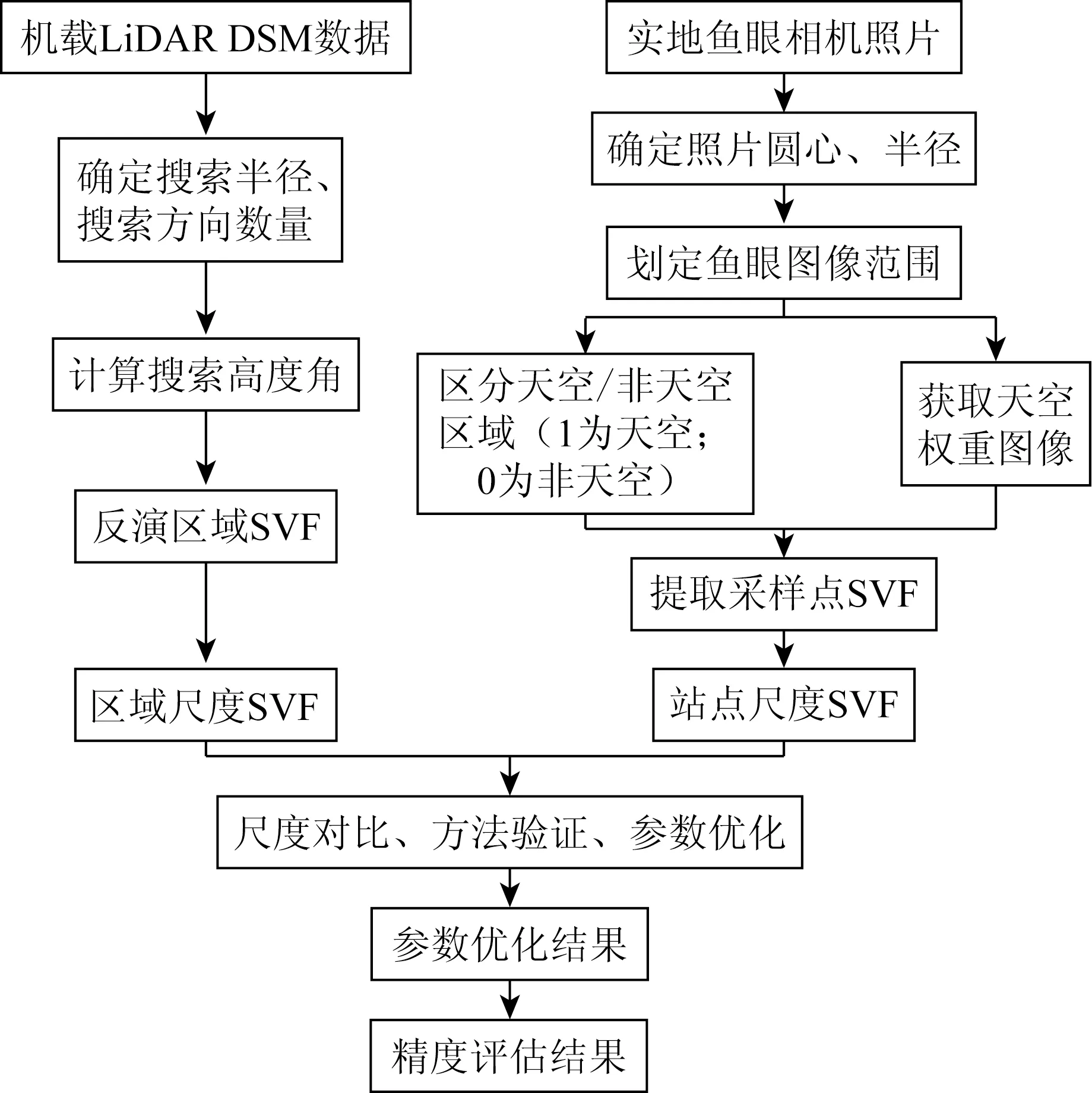
图4 技术路线Fig.4 Technological workflow

本文采用实地鱼眼相片拍摄和机载LiDAR DSM数据反演2种不同方法研究城区复杂下垫面的SVF。在区域尺度SVF的计算中，首先确定机载LiDAR的DSM的搜索半径与搜索方向的数量，然后通过计算搜索高度角来获取区域范围的SVF。在站点尺度SVF的计算中，首先确定鱼眼相片的范围，然后通过计算天空权重图像以及划分天空与非天空来提取采样点的SVF。在“站点—区域”不同尺度的比较分析过程中，不同尺度之间相互联系，“站点尺度”为“区域尺度”提供方法验证和参数优化等支持，不同尺度的对比、方法验证和参数化方案的优化，可以有效地提高SVF的遥感估算精度。

3 结果与分析

3.1 利用DSM提取SVF分布

根据上文提到的利用DSM提取SVF的方法，获得不同搜索半径、搜索方向数量下SVF的分布情况(图5)。如图5所示，该区域SVF具有一定的分布规律。在道路、水体、公园和空地等空旷区域SVF较大，呈现红色、橘红色色调，在奥林匹克公园以及奥林匹克森林公园处尤为明显； 在居民区等建筑物密度较大区SVF较小，呈现浅黄色或者绿色色调。当搜索方向数量不变，搜索半径增大时，SVF较高的红色区域逐渐缩小，SVF较低的浅黄色与绿色区域逐渐增多，表示SVF随着搜索半径的增大而减小。

(a) 搜索半径为20个像元 (b) 搜索半径为50个像元 (c) 搜索半径为80个像元

图5 搜索方向为32个像元时不同搜索半径所计算得到的SVF

Fig.5CalculatedSVFvalueswhenthenumberofsearchdirectionsis32withthedifferentsearchradii

图6为搜索半径为50个像元时，搜索方向数量为8，16，32个时SVF计算值的比较。由图6可以看出，整体上搜索方向数量越多，SVF计算值越小，当搜索方向数量取32个时SVF计算值最小，当搜索方向数量为8个时SVF计算值最大，3种情况下的SVF相近。当搜索半径大小相同，搜索方向数量取16和32个时，由DSM提取的SVF相较于8个搜索方向提取的SVF更接近，综上情况可以得出，当搜索方向数量超过16个时，搜索方向个数对SVF计算值的影响较小。

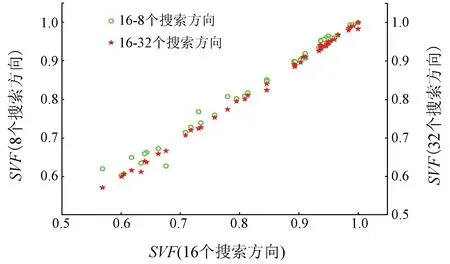
图6 搜索半径为50个像元时的SVFFig.6 SVF values when search radius is 50 pixels

3.2 鱼眼相机SVF采样分析

表1为48个采样点的SVF计算结果。

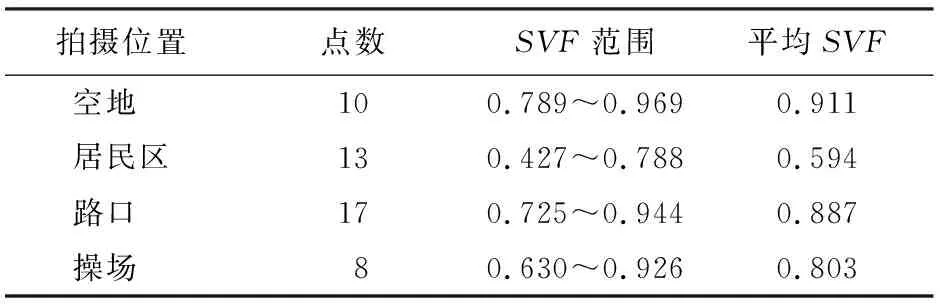
表1 采样点的SVF计算结果Tab.1 Calculation results of the SVF of sampling points

由于下垫面环境复杂，不同下垫面、不同建筑物密度的区域，SVF不同。按下垫面类型的不同，选择了4种具有代表性的区域作为采样位置，包括空地、居民区、路口和操场。其中，最大的SVF为0.969，位于空地区域； 最低的SVF为0.427，位于居民区。在建筑物密度较高的居民区，SVF相对较小，平均SVF为0.594； 空地、路口和操场的建筑物密度较低，SVF值相对较大，平均SVF分别为0.911，0.887和0.803。

3.3 利用DSM提取SVF验证分析

以鱼眼相片计算所得的SVF为验证数据，分析DSM提取的SVF结果精度。在搜索方向数量为32个时，分别取搜索半径为50，80，100个像元，比较DSM提取的SVF与鱼眼相机测量计算得到的SVF。结果如图7所示。

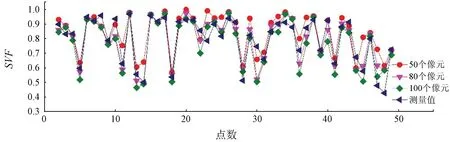
图7 2种方法SVF比较Fig.7 Comparison of SVF values of two methods

整体上，随着搜索半径的增加，SVF减小，鱼眼相机测量的SVF与DSM提取的SVF变化趋势相同，且SVF值也相近。

为进一步验证分析，在搜索方向数量为32个时，将在不同搜索半径下DSM提取的SVF与外业测量的SVF分别进行线性回归拟合，结果如图8所示。

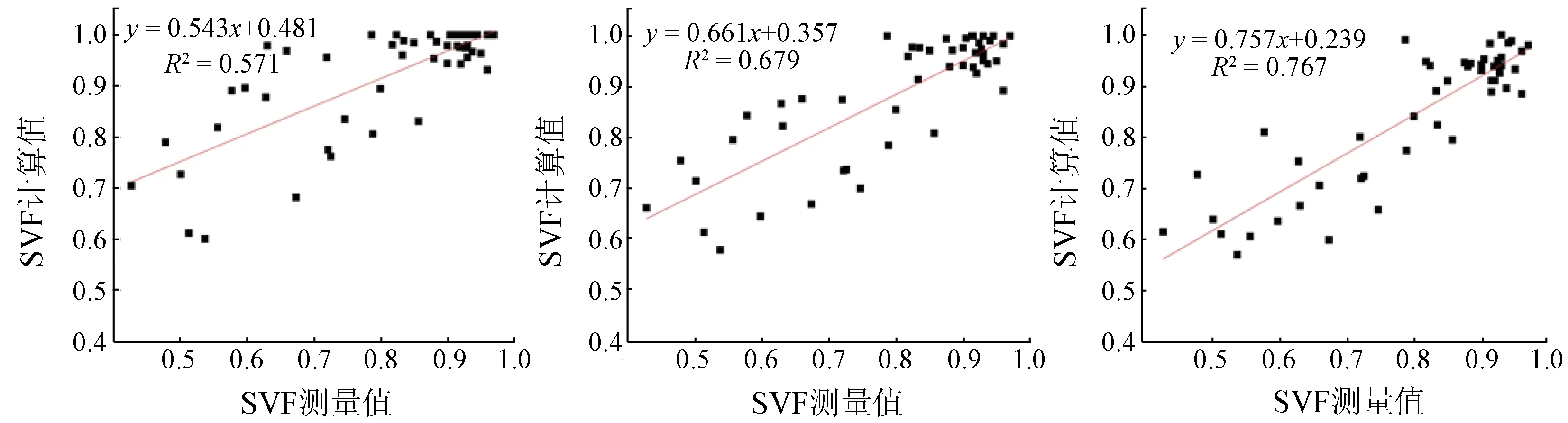
(a) 搜索半径为20个像元 (b) 搜索半径为30个像元 (c) 搜索半径为50个像元

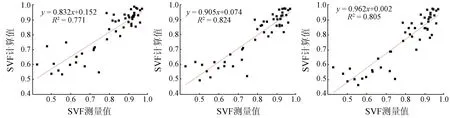
(d) 搜索半径为65个像元 (e) 搜索半径为80个像元 (f) 搜索半径为100个像元

图8 不同搜索半径下2种方法线性回归拟合

Fig.8Linearregressionfittingoftwomethodswithdifferentradii

通过观察分析图 8，可以发现，由DSM计算所得的SVF与鱼眼相机拍摄得到的SVF具有一定的线性相关关系。随着搜索半径的增大，决定系数R2先增大后减小，在搜索半径为80个像元时取得最大值，即搜索半径为80个像元时拟合效果最佳。

为进行全面比较，求解出不同搜索半径、不同搜索方向数量下DSM提取的SVF与鱼眼相片计算得到的SVF之间的均方根误差(root mean square error,RMSE)，进行综合比较分析，得到RMSE的变化趋势图(图9)。

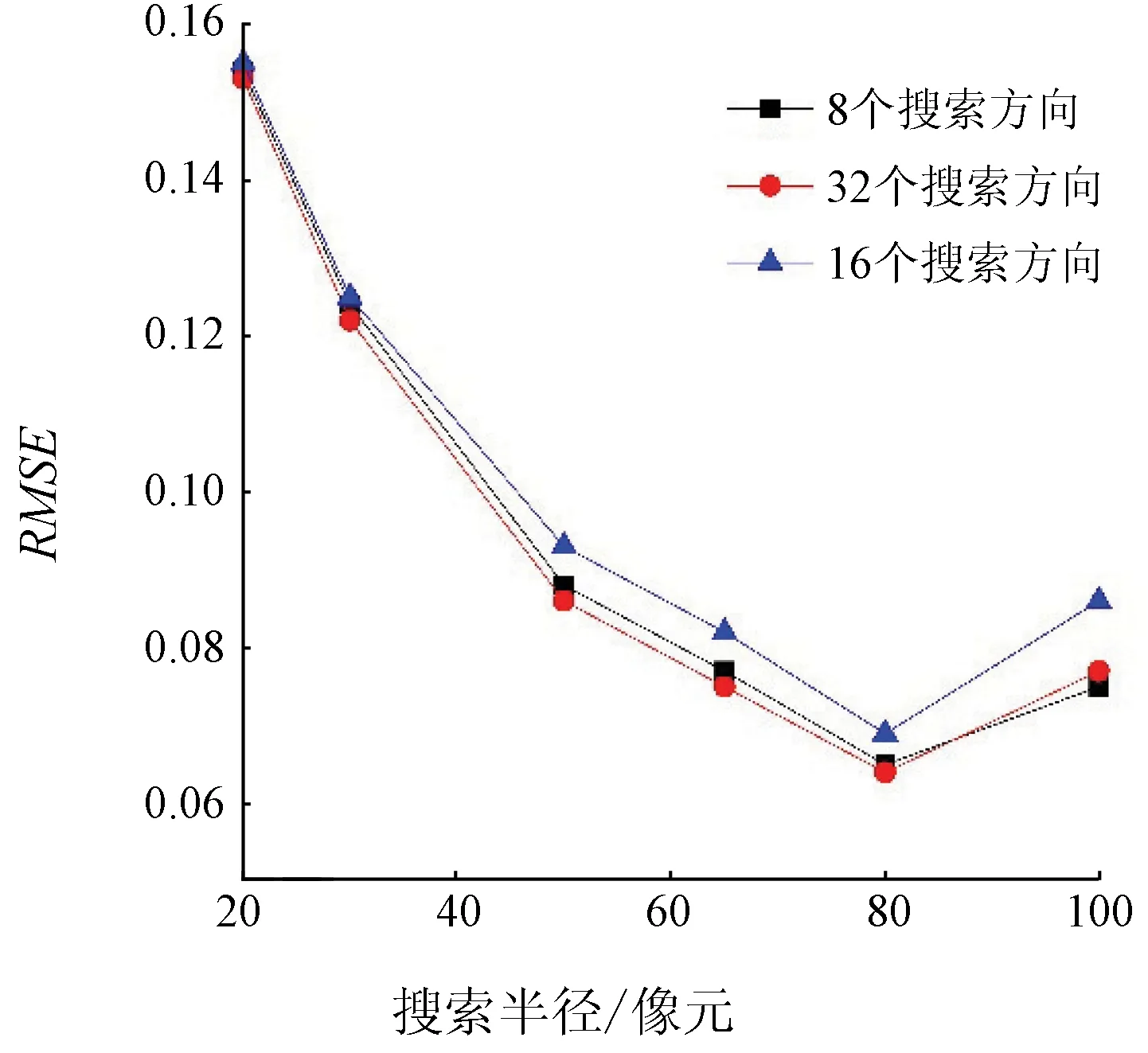
图9 不同搜索半径、搜索方向数量下的RMSE趋势Fig.9 Trend of RMSE with different searchradii and number of search directions

如图9所示，在搜索半径不变时，16和32个搜索方向的RMSE基本相同，8个搜索方向的RMSE较大； 搜索方向数量不变时，随着搜索半径增大，RMSE先减小后增大。在搜索方向为8个、搜索半径为20个像元时RMSE最高，为0.155，在搜索方向为32个、搜索半径为80个像元时RMSE最低，为0.064，所以前者DSM计算得到的SVF与鱼眼相机提取的SVF偏差最大，后者DSM计算得到的SVF与鱼眼相机提取的SVF偏差最小。

综上所述，当搜索方向为32个、搜索半径为80个像元时，DSM计算所得的SVF与鱼眼相机测量计算得到的SVF最接近，由DSM提取的SVF结果最准确。

4 结论

本文利用DSM数据计算城市地区复杂下垫面的SVF，以北京市鸟巢周边地区为例，分析了在不同数量的搜索方向、不同搜索半径下的SVF，并实地拍摄采样点的鱼眼相片，计算采样点的SVF，以利用鱼眼相片采样提取的SVF作为验证数据，对DSM提取城市SVF进行参数化方案的优化，并评估分析 DSM提取城市SVF方法的结果精度。具体结论如下：

1)利用DSM数据计算的下垫面SVF受搜索半径大小、搜索方向数量的影响。SVF随着搜索半径的增大而减小，在搜索半径为80个像元即40 m时SVF最准确； SFV随着搜索方向数量增加而减小，选择32个搜索方向时计算的SVF最准确。

2)当搜索方向为32个、搜索半径为80个像元时，R2取得最大值，且RMSE最低，为0.064，即在该参数下由DSM计算所得的SVF与鱼眼相片计算得到的SVF最接近，由DSM提取的SVF结果最准确。

3)通过2种方法的比较，得到在一定的范围内，两者具有一定的线性相关关系，表明利用DSM计算大范围城市下垫面SVF的方法具有一定的可行性。

本文提出了在城市地区利用DSM数据计算城市地区复杂下垫面的SVF，并利用鱼眼相片计算SVF，对2种方法进行研究分析，获得了一些初步的结果。同时本研究也存在相应的不确定因素。一是树木等非建筑物的影响，这可能导致SVF计算结果的部分偏差； 二是影像的空间分辨率会影响估算的SVF，本文选取的影像空间分辨率为0.5 m，未分析其他空间分辨率影像的情况。在后续的进一步研究中需考虑不同空间分辨率的数据对SVF的影响，深入分析不同数据尺度下采用DSM数据计算SVF方法的可行性。