玻璃成分–结构–性质的“基因结构”模拟法

张丽艳, 李洪, 胡丽丽, 王亚杰,3

玻璃成分–结构–性质的“基因结构”模拟法

张丽艳1, 李洪2, 胡丽丽1, 王亚杰1,3

(1. 中国科学院 上海光学精密机械研究所 高功率单元技术实验室, 上海 201815; 2. 日本电器玻璃株式会社, 谢尔比 北卡罗莱纳州, 美国 28150; 3. 中国科学院大学, 北京 100049)

介绍了一种基于玻璃结构性质而建立的玻璃成分(C)–结构(S)–性能(P)的统计模拟方法。分析了常用的成分–性质(C-P)模拟法的局限性以及结构–性质(S-P)模拟法的特点, 并利用磷酸盐激光钕玻璃化学稳定性改良实验比较了C-P与S-P模型的差异, 表明对于组分微调设计, 结构模拟可以给出更好的模拟结果。叙述了C-S-P模型的建模步骤, 通过模拟案例演示了使用C-S与S-P模型反演玻璃成分的具体过程。除常规性质外, C-S-P模拟法还可以对玻璃的光谱激光性质及化学性质等C-P模型难以准确模拟的性质进行预测和模拟。目的是探索一种对玻璃设计普遍适用的, 可以为新型玻璃的研发和玻璃工业生产提供高效、准确设计的便捷模拟方法。

玻璃基因结构; 统计分析建模; 成分–结构–性质模型

准确的材料性质模拟预测是新材料发展的方向[1]。玻璃作为一种热力学亚稳态材料, 在玻璃成分和性质之间建立的数学函数关系, 即C-P关系的统计建模方法已被广泛应用于学术研究和商业玻璃行业中[2-4], 如玻璃纤维, 核废料固化玻璃等[5-6]。但是对于大多数玻璃体系而言, 玻璃复杂的组成、层出不穷的新玻璃探索以及多变的成分设计思路, 如多种网络形成体共存, 离子型或非氧化物玻璃系统, 多变的原料品种等, 使得C-P模型的模拟精度达不到设计要求, 这一定程度上与玻璃的无定型结构特性有关。商业玻璃数据库, 例如SciGlass和INTERGLAD, 虽然涵盖了数千个玻璃配方和相应的基本性能, 但其本质是配方的积累和基于玻璃组成氧化物特点而进行的玻璃性质的简单估算, 并不具备准确的C-P预测功能。迄今为止, 没有哪一种数据库可以提供玻璃的结构–性质(S-P)之间, 尤其是光谱或强度/模量/化学性质–玻璃结构之间的内在关联信息, 以满足不同性质要求的新型玻璃材料的设计。因此, 从玻璃的实际应用设计角度来看, 目前没有新的手段可以用来进行玻璃材料准确的预测设计与性能改良。长期以来, 实用性复杂玻璃体系的设计都是在很多先前的经验积累上和在较狭窄的玻璃组成空间范围内调试, 以取得在玻璃性能上的渐进式改良。这种方法不仅实验量大、速度缓慢, 且具有一定的盲目性。那么, 如何对多组分玻璃体系进行较为精准的模拟设计, 且模拟方法不受玻璃性质是否呈线性变化的限制, 将是一个很有意义的研究课题。

复杂玻璃系统的组分与网络结构及相关性能的研究工作较少, 存在诸多挑战, 但对用“结构改良”的方式来设计复杂玻璃系统从而满足更高的应用和生产性能的需求是至关重要的。因此, 要设计准确的多组分玻璃的性能和组成, 新方法的探索和建立是必要的。以目前的检测方法能提供的结构信息为基础, 精确解析和定量测量玻璃的基本结构变化, 通过以此为基础建立的数据库, 对玻璃结构进行所需的改良设计, 从而使设计的新玻璃达到应用和生产工艺所需的更高标准。这种新的从玻璃结构入手的设计开发途径类似目前医学和医药界正在快速推动的基因库开发与基因治疗。

以激光玻璃为例, 激光玻璃的设计多年来一直希望摆脱传统的经验设计模式, 能够对激光玻璃的光谱性质进行较为准确的预测, 缩短玻璃的研发时间, 并降低研发成本, 同时要求开发超宽带、高频率激光玻璃应用于未来的高能物理和清洁核聚变发电等。此外, 由于高强度高模量玻璃纤维的熔制和拉丝温度极高, 使其产量低、成本高, 导致该类产品开发停滞已数十年。如何保持或提高其玻璃性能并降低生产温度急需新的玻璃设计思路。那么, 从结构设计和改良入手研发新型高强度、高模量玻璃纤维, 对国防和航空应用也具有重要意义。

随着近年来研究玻璃“中程”结构技术手段的不断发展和完善[7-9], 能否用数理统计模拟的方法将激光玻璃结构信息和玻璃的性质以及组分设计相结合, 即将玻璃成分–结构–性能的大量数据用数理统计方法整合为一体, 进而找出用目前常规方法难以发现的玻璃成分–结构–性质的关系模型。利用现有的结构测试分析方法, 获得并精确解析所研究的玻璃系统从简单到复杂组分的结构变化规律, 归纳并进行玻璃成分–结构–性质的统计模拟, 建立三者之间相关性的模拟模型及模拟公式, 进而达到可以根据结构信息准确模拟新型玻璃性质的目的。这种新方法可为探索新型玻璃提供新的思路, 为玻璃研究人员对玻璃的“分子”或“结构单元”设计改良提供可靠的手段。可以更为准确地通过结构信息预测成分对目标性质的影响, 大大缩短新型玻璃的研发周期。具体方法为: 利用各种结构测试手段, 如核磁共振(NMR)、电子顺磁共振波谱(EPR)、拉曼光谱(Raman)、红外光谱(IR)和X射线光电子能谱分析(XPS)等, 采用综合测试方法确认相关玻璃中的各种玻璃结构单元; 研究结构单元对特定性能的影响规律, 从而确定玻璃成分–结构–性能之间的量化关系模型; 利用这种模型, 可以迅速设计所需性质的玻璃组分; 再通过组分验证实验进一步补充数据库, 不断修正模型, 最后达到准确预测的目的。多种测试方法综合运用的优势在于可在更好地解析玻璃结构的基础上建立更为准确的结构模型, 如P5+、Al3+两种离子进行结构建模时, 根据NMR研究结果, 则还需考虑P-O-Al的关联作用和相互影响; 如建立磷酸盐玻璃中Yb3+离子的结构模型, NMR证实了Yb3+、P5+之间几乎不存在键合, 因此不必考虑P-O-Yb之间的交联等等。类似于氟磷玻璃这类非氧化物玻璃系统, 由于原料的多变性(如引入磷的原料可以根据具体要求使用磷酸盐、偏磷酸盐及磷酸二氢盐)、玻璃结构的特殊性、高挥发性和易析晶特点, 导致其成分–性质模拟的精度低, 运用结构模拟则可得到较好的预测结果。

将上述这种基于玻璃结构信息而建立的模拟方法运用到稀土掺杂的磷酸盐玻璃的组分–红外/拉曼结构–光谱性质的预测中, 其实验结果与预测结果的高度重叠性证实了这种方法的可靠性与准确性, 首次展示了复杂的玻璃激光性能可以通过少数特征结构或特征“基因”来进行线性模拟[10]。

本研究对结构模拟法的建模原理和步骤进行了重点阐述, 并介绍了C-P和S-P模拟方法各自的特点。通过几组模拟案例比较了C-P与S-P模拟在预测精度上的差别。玻璃成分–结构–性能模拟法的最终目标是依据玻璃结构信息建立一种可靠的模拟方法, 使得实用玻璃设计变得更加高效、迅捷、准确。

1 数理统计模型的建模原理

文献[11]详细叙述了数理统计模拟建模的基本方程。众所周知, 在晶体和金属材料基因库研究中广泛应用的第一性原理不适用于预测具有多组分和复杂结构特性的玻璃材料。康奈尔建立了一个简单而实用的组分–性质模型公式[12];

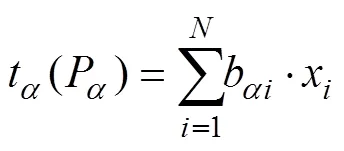
该公式可称为一阶模型公式, 其中b是第个属性的第个分量系数,t是属性P的变换或恒等变换(即不变换),x是第个组分的质量(摩尔)分数。如果玻璃中的各个组分被限制在足够窄的成分范围内, 则组成的非线性函数可以近似为具有可接受误差的线性函数; 若是成分在更宽的范围内变化, 则一阶模型可能不足以接近真实的非线性关系。在这种情况下, 需要非线性逼近函数, 也就是建立二阶模型公式。在多项式模型中, 二阶模型包括二次项和交叉乘积项, 如:

其中b是第个属性的第个分量的平方的系数,b是第个属性的第个和第个分量的叉积的系数。运用公式(2)建立模型的原则是不能使用所有交叉乘积项[13-15]。

1.1 成分-性质(C-P)模型

在常用的C-P模拟中, 公式(1)的运用最为简单普遍。根据文献中已有的或者实验中获得的某一系统玻璃的成分–性质数据, 建立二者之间的线性统计关系; 根据建立模型设计的玻璃成分进行实验, 所得测试数据补充进数据库进行模型修正。为获得较为可靠的C-P模型, 需要注意以下几个问题:

1) 制备较大的玻璃样品, 注意原料称量准 确性;

2) 稳定一致的玻璃制备工艺, 如熔制过程时间控制、挥发损耗、通气或除水时间等等;

3) 玻璃的光学均匀性高(特别针对光学玻璃与激光玻璃);

4) 性质测量的准确度高;

5) 在配方中不宜使用两组分(比如P2O5和Al2O3)相互取代式玻璃成分设计法。

组分–性质模型在模拟某些物理性质、热性质和机械性质时较模拟光谱性质和化学性质更为准确。发射截面、有效线宽、荧光寿命等性质与稀土离子的近–中程环境有密切关联, 而化学稳定性的测量从测试精度上来说误差相对较大。因此, 基于成分和性质变化而建立的一阶线性模型很难对这类性质进行准确模拟。

公式(2)虽然可以得到更“美观”的模型, 但因其交叉项的选取缺乏判断依据, 所以C-P关系二阶模型的实用性较差。虽可依靠某些结构信息判断某两种氧化物之间有结构交联或相互影响, 如根据P–O–Al键可选择P2O5和Al2O3交叉, 然而, 一旦成分中出现两种引入Al3+的原料, 如AlPO4和AlF3, 则模拟系统无法判断Al3+来自哪种原料, 因此很难在后续的玻璃设计中对AlPO4和AlF3的具体使用配比上给出确定而合理的建议, 除非将某种特定的比例约束条件引进C-P模拟数据库。这种确定共含Al3+原料的合理比例关系必须在建立该C-P系统之前, 采用系统的、各组分单一变化的系列玻璃样品的制备方法和测试进行确定。对多数玻璃的应用, 需要同时监测玻璃析晶性能, 以防出现在制备玻璃小样时性质均符合, 但放大生产中有玻璃析晶的不良影响。可以利用已有的大量数据建立成分–性质模型, 但很难保证这些玻璃在熔制和性质测试的时候是完全一致或者准确的, 即保证成分和性质的准确性。尤其值得强调的是, 玻璃设计中常用的取代方法(如磷酸盐玻璃中用部分SiO2取代P2O5), 在建立C-P模型时会面临一些问题。因为系统无法判断玻璃性质的变化是由SiO2还是P2O5的改变引起的, 所以造成模型的精准度较差。

1.2 结构–性质(S-P)模型

结构–性质的建模原理是将公式(1, 2)中的玻璃组成项换成玻璃网络结构单元的相对“浓度”, 或相对分布, 从而建立结构和性质关系模型。这意味着玻璃由一组网络单元组成, 每个网络单元具有统计意义上独特的结构特征, 并且成比例地影响玻璃性质。S-P模型具有如下特点:

1) 玻璃结构测试的准确度高, 组分称量误差的影响小;

2) 结构信息的综合运用可以更好地建立二阶S-P模型(如混合碱效应, NMR证实的稀土掺杂磷酸盐玻璃中为P–O–Al键合而非P–O–RE键合等等), 故此, S-P的二阶模型具有较好的实用性;

3) Raman、IR 等常用结构测试方法快捷方便, 可以获取较为准确的结构信息;

4) 复杂玻璃系统的设计目标性质可以通过结构特征基团(玻璃基因)来锁定;

5) 对非线性光谱激光性质、化稳性质等, S-P模型依然可以做到准确模拟。

另外, 若非必要, 不必将用于模拟的IR和Raman光谱的各个分峰做具体的振动单元归属。因为统计模拟只将各个振动峰积分面积的变化作为模拟要素, 而不需要明确每个峰是由什么键的振动造成的。

1.3 成分–结构–性质(C-S-P)模型的建模过程

结构模拟的最终目的是要得出能很好地符合所设计性质的玻璃成分, 因此, S-P模型要和成分之间建立联系来设计最终的目标玻璃配方, 具体建模步骤如下:

1) 建立成分–结构(C-S)模型;

2) 建立结构–性质(S-P)模型;

3) 根据所需要设计的玻璃性质, 利用S-P模型反推对应的玻璃结构;

4) 根据第三步得到的玻璃结构, 利用C-S模型反推该结构对应的玻璃组分, 并由此建立起C-S-P模型关系;

5) 根据设计组分制备玻璃, 将所有结构及性质信息补充进数据库以完善模型。

所有玻璃结构分析手段皆可以按照以上方法进行C-S-P建模。如利用文献中搜集的碱土金属磷酸盐玻璃的NMR数据(Q基团和化学位移ISO)建立的C-S-P二阶模型可以预测混合碱土金属效应, 转变温度、弹性模量等性质的实测结果与模拟结果有很好的契合[16]。

2 C-S-P模型模拟案例

2.1 激光钕玻璃化学稳定性的改良设计—无规律实验数据的结构建模

在复杂玻璃系统的实验中经常遇到无规律可寻的实验结果, 其成因是多方面的, 如计算、称量、熔制或测试等各个环节。结构模拟可以把实验中无规律的实验结果进行准确的分析和利用。

在基础激光钕玻璃Baseline(BL)中分别引入少量的SiO2(0.5wt%, 1.0wt%, 1.5wt%, 2.0wt%)、B2O3(0.5wt%, 1.0wt%, 1.5wt%, 2.0wt%)和La2O3(1wt%, 2.0wt%, 3.0wt%, 4.0wt%), 以改善其化学稳定性, 并保持BL玻璃的某些基础性质, 如折射率d、非线性折射率2、膨胀系数及转变温度g等不会恶化。表1为样品玻璃的编号及性质。每个样品配置800 g N41型钕玻璃粉料外加相应重量百分比的外掺组分, 如S1为800 g N41粉料+0.5wt% SiO2, 即4 g SiO2, L4为800 g N41粉料+32 g La2O3等。配合料混合均匀后置于石英坩埚内, 在1150 ℃的熔炉中预熔并进行1 h的除水, 后倒入铂金坩埚中搅拌均化6 h后, 降温至900 ℃浇注于预热的铸铁模具上成型, 于马弗炉中退火后, 进行加工及性能测试。所有玻璃样品的制备、加工和测试过程相同, 以保证实验结果的可比性。

表1 实验玻璃编号及性质

*WL=Weight Loss

从实验结果可以看出, 三组玻璃十二次实验, 得出的数据无法指导BL玻璃究竟要如何进行组分微调才可以达到改善化学稳定性的目的。为此进一步进行了各样品的拉曼和红外光谱测试, 使用文献[10]的解析方法, 对结构数据进行系统处理及解析。然后根据C-S-P建模方法, 建立了BL改性实验样品的玻璃成分预测模型。以引入SiO2样品的拉曼光谱为例, 图1为BL玻璃与四个玻璃样品的拉曼光谱及分峰情况, 共有11个单峰。图(b)为拟合误差, 图(c)为虚框处的拟合细节。图1(c)也显示了看似平坦的谱线, 实际存在很多细微的结构差异。图2为12个样品与BL玻璃的拉曼光谱分峰拟合后各分峰积分面积的变化。由图可以看出, 相比于BL基础玻璃而言, 虽然引入的氧化物量很少, 但仍然可从结构光谱曲线中获得大量的结构变化信息。这些结构信息的变化是很好的建模数据, 表2所示为各样品拉曼光谱分峰的积分面积。

使用商业统计模拟软件JMP建立C-P和S-P模型, 均方根越接近于1, 则模型精度越高。图3以最关键的样品失重百分比(化稳性)为例分别建立了两种模型。显然, C-P模型的收敛性差, 模拟精度非常低,(线性回归系数平方)仅有0.66, 表1的结果也证实了这一点; 而S-P模型的达到了0.97, 模型收敛性好, 后续的模拟过程不再一一描述。

图1 BL与含SiO2的玻璃拉曼光谱对比(包含测试与拟合谱图对比)及BL拉曼分峰结果细节描述(a~b)为拟合误差, (c)为虚框处的拟合细节

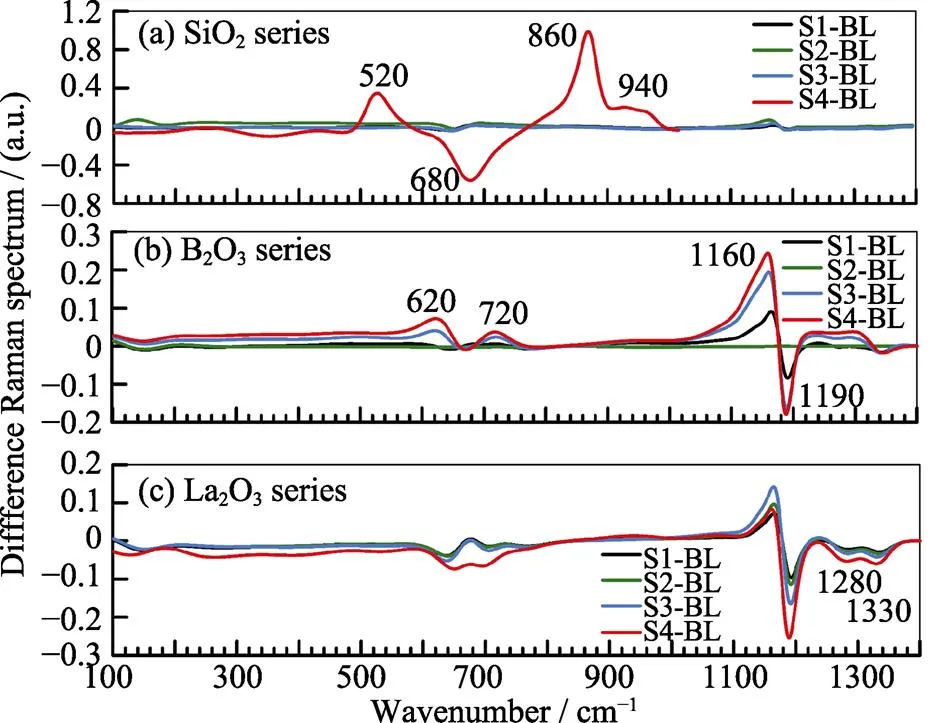
图2 SiO2、B2O3和La2O3对BL玻璃拉曼光谱强度的影响

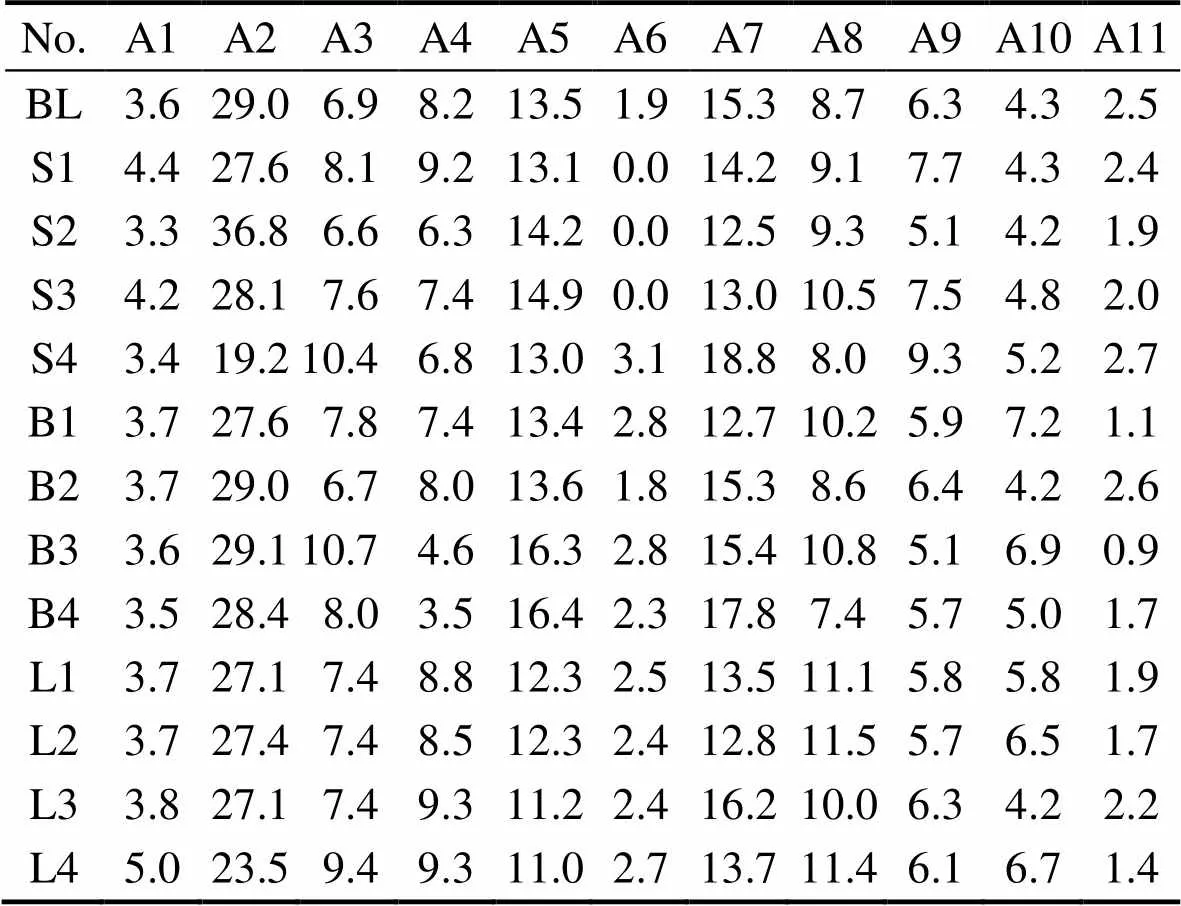
表2 拉曼光谱分峰拟合后各分峰的积分面积(A=Area)

图4给出了S-P模型各性质的预测值与实测值的比较。结果显示, 除了个别明显有疑问的结果外, 整体模型的模拟精度较好。根据该模型, 可以进行新玻璃的成分设计。例如设计化稳性≈0.9 mg/cm2, CTE≈12.2´10–6/K,2≈1.03´10–13esu,g≈488 ℃,d=1.503的玻璃, 则其建议玻璃成分及相应性质列于表3。模型中明显偏离预测范围的点, 在重测性质后如果实测性质没有改变, 则有两种方法可以辨识其误差来源。第一种是直接将其结构信息代入C-S模型, 反推该结构应该对应的组分是什么; 第二种方法是将其实测性质代入S-P模型, 反推关键结构单元后, 再用C-S模型刻画成分信息。如果性质测试结果验证后确实是正确的, 那么这类反常点的异常来源多为玻璃成分误差。为避免异常点数据影响模型精度, 较好的做法是将其从建模数据中剔除, 重新规划模型, 这样反推得到的玻璃成分会更准确。这亦是结构模型可以纠正实验误差的一个重要作用, 也是成分模型无法实现的功能。

图3 化学稳定性的(a)C-P与(b)S-P拉曼模型

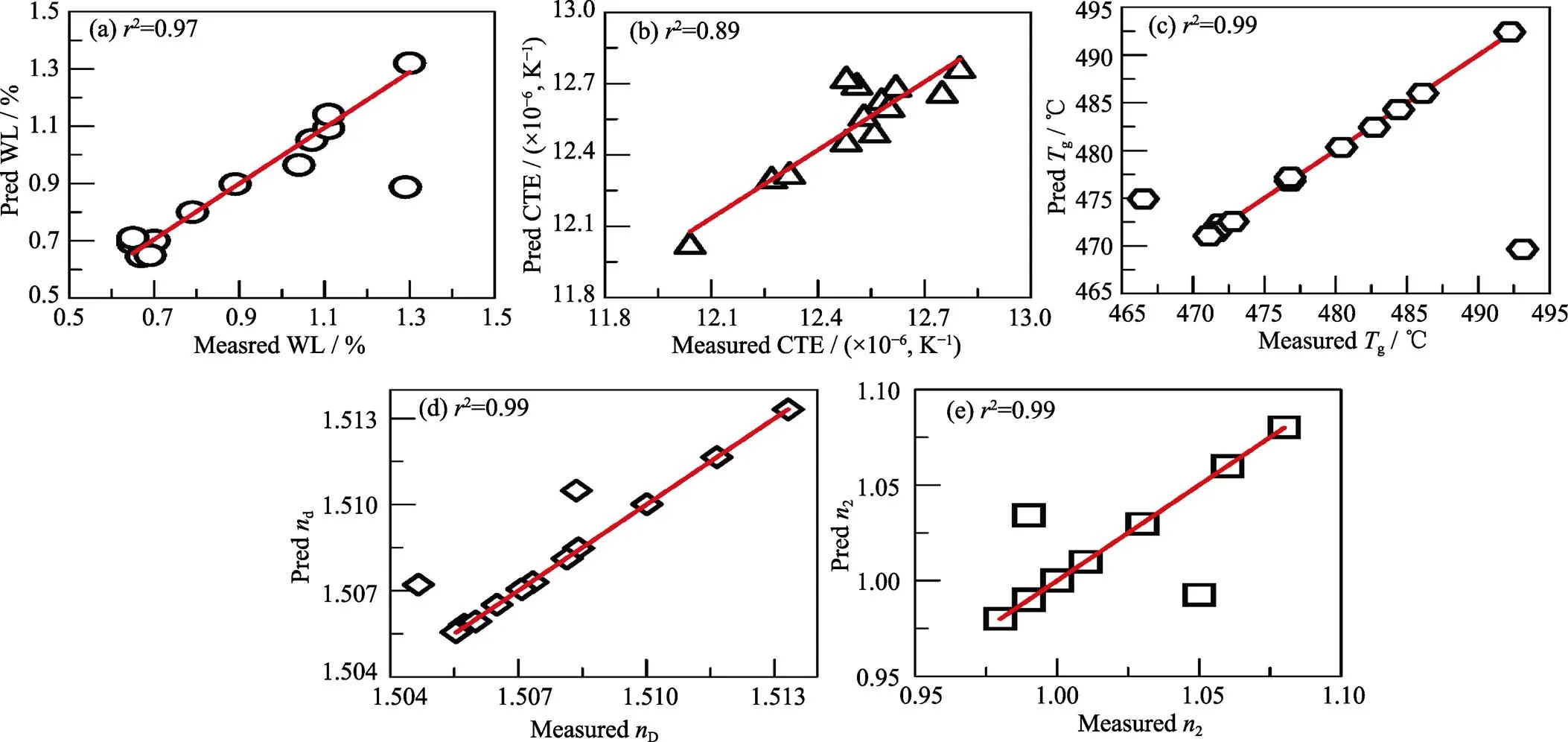
图4 基于S-P模拟的BL化稳性改性玻璃预测值与实验值的比较

*RO and R2O represent specific alkaline earth metals and alkali metal oxides, respectively

2.2 掺镱磷酸盐激光玻璃的光谱性质改性模拟设计

文献[10]详细叙述了如何在GeO2改性的掺镱氟磷玻璃中进行光谱性质结构模拟的全部过程, 也是首次报道的使用结构基因模拟法成功进行复杂玻璃系统准确预测光谱性质的研究。这里以C-P模型难以模拟的取代型玻璃系统(70-)P2O5-10B2O3- 10BaO-3Al2O3-3Nb2O5-4K2O-SiO2-1.25 Yb2O3(= 0, 2, 5, 10, 20) (PS玻璃)为例, 说明C-S-P模拟法的实用性。以红外光谱为例, 对所有样品进行性质和结构测试和光谱分峰(共分出15个子峰), 并计算各分峰的积分面积1-15。为了简化演示过程, 表4仅列出了对PS玻璃设计最重要的性质, 分别是发射截面、转变温度和Stark分裂, 并标出了样品根据ICP测试结果计算的样品中Yb3+离子的浓度。

以=0、2、5和20的玻璃进行结构建模, 以=10的玻璃为验证样品。对=0、2、5和20的玻璃进行红外分峰处理, 得到与表2类似的各分峰积分面积。依据这些结构信息分别建立C-S及S-P模型, 然后设计目标性质为g=503 ℃,emi=0.53 pm2, Stark splitting=786 cm–1的玻璃成分(即PS10)。如 图5所示, 将所设计性质输入刻画器(玻璃设计基因库), 并赋予所要求的各性质一定允许范围的标准偏差。结果显示, 在模拟意愿达到0.99911(即99.911%的设计可行性)的时候, 玻璃的性质应为g= 501.5 ℃,emi=0.5306 pm2, Stark splitting=786.3 cm–1, 此时的SiO2含量应该为10.13mol%, 这非常接近PS10样品中的SiO2=10mol%的实际值。

作为比较, 图6给出了该目标性质的C-P模型设计结果。图6(a)是设计成分SiO2的含量为10mol%时对应的设计性质, 可见模拟意愿仅为0.7, 所需性质无法满足要求。图6(b)是提高模拟意愿到最高值, 此时SiO2的含量为13mol%, 模拟意愿为0.85, 性质同样无法达到设计要求。C-P模型的模拟结果甚至不如从成分–性质线性关系中直接量取的数值, 如图7所示。

图5 由模拟器设计的满足设计性质的玻璃特定结构基团组分(Ai)

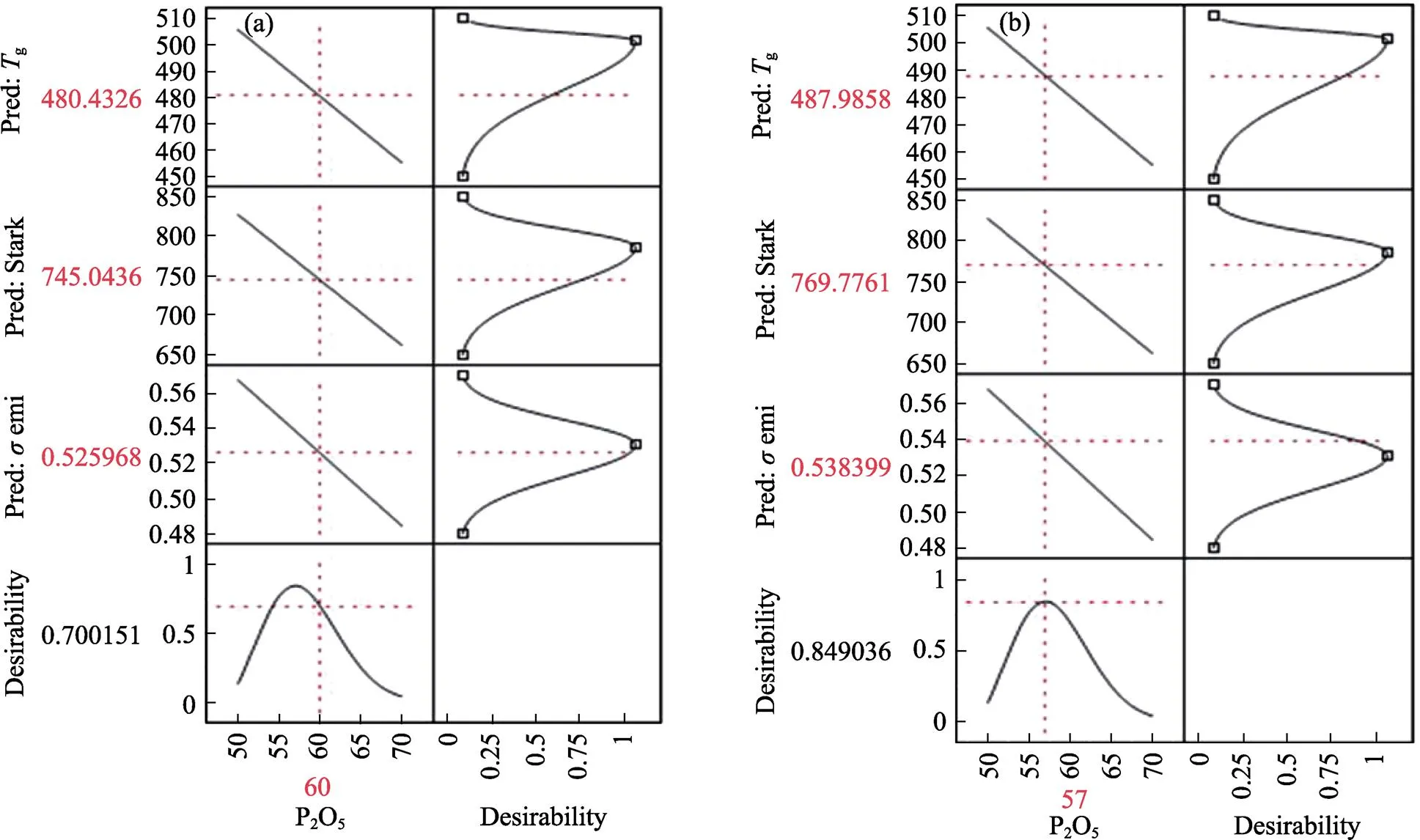
图6 设计成分为SiO2=10mol%时对应设计性质(a)和最高模拟意愿对应的P2O5值对应性质(b)的C-P模型图

图7 Tg、Stark分裂和发射截面的线性估计值

3 结论

本工作提出了一种玻璃的“基因结构”模拟设计法, 简称C-S-P模拟法。该方法利用玻璃的结构信息构建成分和性质之间的关系, 建立成分–结构–性质模型, 进而准确设计符合目标性质的玻璃成分, 达到智能玻璃设计的目的。这种方法不仅可以运用于系统的玻璃模拟数据库的建设, 而且在常规的玻璃实验中亦可方便使用。拉曼和红外光谱能够提供很好的结构模拟要素, 并以磷酸盐激光钕玻璃的化学稳定性成分微调改进实验的无规律实验结果, 同时以改进掺镱磷酸盐玻璃光谱性质实验为案例, 演示了C-P与S-P模拟的差异以及C-S-P方法的模拟过程。除常规性之外, C-S-P模型可以对C-P模型难以模拟的、具有非线性变化特点的光谱激光性质和化学稳定性等进行准确模拟和预测, 并且不受玻璃成分设计方式的限制。每一种玻璃系统的C-S-P模型数据库皆可逐步采集、补充及完善, 以此推进玻璃材料的高效、迅捷、准确的设计进程。具体的建模演示除文献[10, 16]外, 将在后续文章中做进一步介绍。

[1] ZHAO J C. A perspective on the materials genome initiative., 2014, 36(2): 89–104.

[2] VOLF M.Mathematical Approach to Glass. Amsterdam: Elsevier Science Publishers, 1988.

[3] LI H, DAVIS M J, URRUTI E H. Eye-safe laser glass development at SCHOTT., 2010, 7686(16): 1–12.

[4] VIENNA J D. Compositional models of glass/melt properties and their use for glass formulation., 2014, 7: 148–155.

[5] LI H, CHERYL R, WATSON J. High-performance glass fiber development for composite applications., 2014, 5(1): 65–81.

[6] VIENNA J D, HRMA P R, SCHWEIGER M J,Effect of composition and temperature on the properties of High-Level Waste (HLW) glasses melting above 1200 ℃ (Draft). Office of Scientific & Technical Information Technical Reports, 1996.

[7] YAMASHITA H, YOSHINO H, NAGATA K,Nuclear magnetic resonance studies of alkaline earth phosphosilicate and aluminoborosilicate glasses., 2000, 270(1): 48–59.

[8] GREAVES G N. EXAFS and the structure of glass., 1985, 71(1): 203–217.

[9] SEN S, RAKHMATULLIN R, GUBAYDULLIN R,A pulsed EPR study of clustering of Yb3+ions incorporated in GeO2glass., 2004, 333(1): 22–27.

[10] ZHANG L Y, LI H, HU L L. Statistical structure analysis of GeO2modified Yb3+: phosphate glasses based on Raman and FT-IR study., 2017, 698: 103–113.

[11] LI H, ZHANG L Y, HU L L,Statistical Modeling Approach to Glass Research and Development: Composition-Structure- Property Relationships (Invited). 8th International Symposium on Advanced Glass, Shanghai, China, 2018.

[12] CORNELL J A. Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data, 3rd ed. New York: John Wiley and Sons, 2002.

[13] DARROCH J N, WALLER J. Additive and interaction in three-component experiments with mixtures., 1985, 72: 153–163.

[14] PIEPEL G F, SZYCHOWSKI J M, LOEPPKY J L. Augmenting scheffe linear mixture models with squared and/or crossproduct terms., 2002, 34(3): 297–314.

[15] SCHEFFE H. The simplex-centroid design for experiments with mixtures., 1963, 25(2): 235–263.

[16] ZHANG L Y, LI H, HU L L. Statistical approach to modeling relationships of composition-structure-property I: Alkaline earth phosphate glasses., 2018, 734: 163–171.

Structure Modeling of Genes in Glass: Composition-structure-property Approach

ZHANG Li-Yan1, LI Hong2, HU Li-Li1, WANG Ya-Jie1,3

(1. Key Laboratory of Materials for High Power Laser, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai 201815, China; 2. Nippon Electric Glass, Shelby, North Carolina 28150, USA; 3.University of Chinese Academy of Sciences, Beijing 100049, China)

A statistical modeling approach to modeling glass composition (C) – structure (S) – property (P) is introduced based on glass property response to the glass network structure. This paper first reviewed some of the limitations of the C-P statistical modeling approach, then followed by complementary benefit identified from using S-P statistical modeling approach. Furthermore, S-P modeling is not limited by a narrower composition space as seen in the C-P modeling case, which benefits glass composition fine-tuning and design optimization, such as in the chemical stability experiment for Nd: phosphate laser glass, the S-P models perform much better than the C-P models. The procedure of C-S-P modeling was illustrated, and how to use C-S and S-P models inverse the composition of glass was also detailed. Except for the regular properties, C-S-P modeling methodology can provide more accurate predictions on laser glass emission properties, chemical durability,., which are often difficult by using the C-P modeling approach alone. Our effort on C-S-P modeling is to explore a general methodology that can provide researchers with an alternative method to facilitate glass design with higher efficiency, fast turn-around, and high accuracy and precision.

glass structure gene; statistical analysis modeling; composition-structure-property model

TQ174

A

1000-324X(2019)08-0885-08

10.15541/jim20180514

2018-10-31;

2019-01-07

张丽艳(1971–), 女, 副研究员. E-mail: jndxzly@hotmail.com