一种基于Costas序列的多输入多输出声纳正交发射信号集设计方法

贾基东， 李淑秋， 高善国

(1.中国科学院 声学研究所， 北京 100190; 2.中国科学院大学 电子电气与通信工程学院， 北京 100049; 3.中国科学院 先进水下信息技术重点实验室， 北京 100190)

0 引言

如何选择发射信号的波形是主动声纳设计过程中必须考虑的问题之一。不同的信号波形具有不同的信号参数，会有不同的处理结果，直接影响声纳的性能[1]。如传统声纳系统常采用单频矩形连续波(CW)脉冲信号、线性调频(LFM)脉冲信号等。其中，CW的短脉冲具有较好的距离分辨力、长脉冲具有较好的速度分辨力，二者不可兼得。LFM利用脉冲压缩技术克服了探测距离和测距精度之间的矛盾，但其距离分辨力不如CW短脉冲、速度分辨力不如CW长脉冲。可见，对于不同用途的主动声纳而言，波形设计工作至关重要。

多输入多输出(MIMO)探测声纳是一种通过MIMO技术规划时空信道，以获取更高声纳探测能力的新型主动探测声纳[2]。相比于传统主动声纳的单输入多输出(SIMO)系统，MIMO声纳具有多个发射单元，能够同时发射多个相互正交的探测波形，在接收端通过相关技术对不同发射信号进行分离处理，从而可以获得更高的检测增益和空时分辨能力。因此，对于MIMO声纳的波形设计工作而言，首先是要找到一组两两相互正交的发射信号集，且具有良好的距离分辨力和速度分辨力。

MIMO技术在探测中的应用引起了众多学者对设计MIMO声纳正交探测波形的兴趣。由于CW信号存在测距精度和传播距离的矛盾，人们尝试找出适合MIMO声纳的宽带探测信号。文献[3]研究了一种正交频分(OFD)LFM信号，这种信号是对传统声纳LFM信号的直接扩展，各个LFM信号分别落在不同的子频带内、形成彼此间的正交性。

文献[4]提出了一种基于Gold序列的相位编码信号。Gold序列由两个m序列优选对通过模2和运算产生，具有优于m序列的互相关函数和多于m序列的序列族数量，但任意长度的m序列优选对并不容易寻找[5]。文献[6]设计了一种码分复用波形，将信号频域和时域划分为等分的子带，在每个时域子带内随机选取子频带和调频正负，从而使信号间相互正交。随机编码的时频编码信号难以进行理论分析，信号集整体性能有待验证。Costas序列由Costas于1984年提出，采用Costas序列编码的跳频信号具有近似理想的时延多普勒模糊函数，受到人们的广泛关注[7-12]。

本文研究了Costas序列在MIMO声纳探测中的应用，提出了一种基于Costas序列的跳频信号集设计方法，以期使信号集正交性和信号集中的信号数量同时达到最优。

1 正交信号集模型

1.1 理想正交信号集

信号集S={s0,s1,…,sN-1}称为一组正交信号集，当且仅当满足：

|χij(τ,η)|=0,i≠j,

(1)

式中：τ表示信号时延；η表示多普勒尺度因子；|χij(τ,η)|表示信号si与sj的模糊函数[13]，

(2)

1.2 OFD-LFM信号

假定sn-1(t)是第n个声源发射的OFD-LFM信号，则有[3]

(3)

1.3 跳频信号模型

跳频信号是信号频率根据序列编码随时间跳变的信号。假定跳频信号子脉冲为CW信号，序列编码为M={m0,m1,…,mN-1}，第n个子脉冲频率为fn=f0+Δfmn，f0为初始频率，则跳频信号s(t)的数学模型描述如下：

(4)

式中：pn表示子脉冲，Ts=T/N表示子脉冲周期；

(5)

上述跳频信号模型实际上是一种在时频二维平面按一定规律构建信号的通式，CW信号、LFM信号都可以视作跳频信号的特例。跳频信号子脉冲时长趋向于0、编码序列码元值依次递增或递减时，跳频信号分别成为正负调频的LFM信号；编码序列仅有一个码元时跳频信号转化为CW信号。

跳频信号的性能与编码序列密切相关。常用的编码序列有M序列、Gold序列[4]、线性同余序列[14]、二次同余序列[15]等。文献[16-17]在1984年提出了Wlech和Golomb两种结构化方法设计Costas矩阵，两种方法都建立在有限域和本原元理论基础上。基于同一素数p构造的Costas序列具有相同的序列长度，按照这些序列编码的跳频信号不仅具有近似理想的自模糊函数，而且同一素数的有限域生成的不同Costas序列间具有一定的正交性，在一定约束条件下可以视作一组正交信号集。

2 Costas序列编码的正交跳频信号集

任意每行每列有且仅有1个元素等于1、其余元素都为0的N2阶矩阵称为置换矩阵。Costas矩阵是一类特殊的置换矩阵，它与自身任意方向的平移副本之间都至多有1个元素1重合，如图1所示。

图1 Costas矩阵Fig.1 Costas matrix

Costas矩阵的定义如下：

定义1N2阶置换矩阵A=[aij](其中1≤i,j≤N,aij∈{0,1})称为Costas矩阵，当且仅当对任意不全为0的整数r,s(|r|≤N,|s|≤N,(r,s)≠(0,0))，以下非循环差异函数满足：

(6)

其中，非循环是指i+r或j+s超出区间[1,N]时ai+r,j+s=0.

2.1 Costas序列生成方法

2.1.1 有限域和本原元理论

设F是一个含有0和1的数集，如果F对于数的四则运算都封闭，则称F为1个数域。用q表示数域F中的元素个数，q=∞时F称为无限域，q<∞时F称为有限域。q也称做数域F的阶，相同阶的有限域都是同构的。可以证明[18]，有限域的阶q=pn，其中p表示素数。有时，将pn阶的有限域称为伽罗华域(Galois field)，记作GF(q)。n=1时有q=p，此时称GF(q)为素域。

对于GF(q)中的元素α，如果GF(q)中的所有非零元素都能由|αn|q表示，其中1≤n≤q-1，则称α为GF(q)的本原元，表述如下：

GF(q)={α1,α2,…,αq-1}，

(7)

其中，省略了对q的取模运算|*|q，以下涉及有限域四则运算时均采用这种省略表述。

下面给出一些有用的性质：

性质1有限域GF(q)中有且仅有φ(q-1)个本原元，其中φ表示欧拉函数，即

(8)

式中：p1,p2,…,pr表示q-1质因子分解的r个不同质因子。

性质2如果α是有限域GF(q)的本原元，则有

αq-1/2=-1.

(9)

性质3如果α是有限域GF(q)的本原元，r1,r2,…,rφ(q-1)表示q-1的欧拉函数所描述的φ(q-1)个整数，则GF(q)的所有本原元可以表述为αr1,αr2,…,αrφ(q-1).

2.1.2 本原元搜索方法

利用本原元的定义和性质，可以得到一种搜索GF(q)的所有本原元的方法，首先搜索GF(q)的1个最小本原元，然后利用性质3生成GF(q)的所有本原元集合。具体步骤如下：

步骤1对于给定的素数p，初始化k=2.

步骤2判断是否满足条件|k(p-1)/2|p=p-1，是则继续步骤3，否则转步骤5.

步骤3计算p-1的欧拉函数φ(p-1)和这φ(q-1)个整数所组成的集合V.

步骤4计算集合E=|kV|p，去掉集合E中的重复元素，判断集合E中的元素个数是否等于φ(p-1)，是则搜索结束，集合E就是素数p的所有本原元组成的集合，否则进入下一步。

步骤5令k=k+1，重新回到步骤2.

2.1.3 Welch-Costas序列的构造

对于有限域GF(q)，其中q=pn，令n=1，则有限域GF(q)变为素域GF(p)，即GF(p)={1,2,…,p-1}。记GF(p)的所有本原元组成的集合为Ep，若α∈Ep，则本原元α生成的GF(p)长度为N=p-1的Costas序列[17]如下：

W1=αj，j=1,2,…,N.

(10)

记GF(p)所有长度为N=p-1的Costas序列组成的集合为Xp，称作序列集Xp. 则Welch结构W1构造了一种集合Ep到Xp的一一映射关系，即GF(p)每个本原元都唯一地生成1个Costas序列，且序列集中共有φ(p-1)个Costas序列，记作|Xp|=φ(p-1)。

2.2 信号集正交性表示

2.2.1 序列集的正交性

跳频信号性能与编码序列密切相关，基于Costas序列编码的正交跳频信号集性能与Costas序列集同样有紧密联系。对于有限域GF(p)的序列集Xp，其中任意2个Costas序列的正交性可以用序列的差异函数描述如下：

(11)

式中：i=j时Cij(r,s)表示序列的自差异函数，i≠j时Cij(r,s)表示序列的互差异函数；s=0时Cij(r,0)称为序列的时延差异函数；r=0时Cij(0,s)称为序列的频移差异函数。

显然，由Costas序列的定义可知，除了C(0,0)，序列的自差异函数C(r,s)≤1，如图2所示，因此用Costas序列编码的跳频信号具有图钉型的理想自模糊函数。相比于传统声纳的发射波形设计，在MIMO声纳中，还关心信号集的互模糊性能，然而任意有限域GF(p)构造的Costas序列互相关性能并不理想。幸运的是，对于一些具有特殊形式的素数序列，由它们的有限域构造的Costas序列则具有相对较好的互相关性能。对于一类形如p=2p1+1的素数序列，其中p1也是素数，称为安全素数。Drakakis等[19]指出，对于安全素数的有限域所生成的Costas序列集合Xp，其中任意2个W1序列的互时延差异函数Cij(r,0)≤2.

图2 Costas序列的自差异函数Fig.2 Self-difference function of Costas code

定义如下序列集时延差异函数图谱：

(12)

则MCp(i,j)图可以清晰地显示出序列集Xp时延差异函数的整体性能。

定义如下序列集时延差异函数最大值函数：

(13)

则可以用MMC(p)表述不同有限域GF(p)序列集Xp互时延差异函数的性能变化。

2.2.2 信号集的正交性

与序列集Xp相对应，信号集Sp的正交性可以用(2)式所示2个信号的互模糊函数表示：η=1时|χij(τ,1)|表示时延模糊函数，τ=0时|χij(0,η)|表示频移模糊函数。

定义如下信号集时延模糊函数图谱：

(14)

则MXp(i,j)图可以用来表示信号集Sp时延模糊函数的整体性能。

定义如下信号集时延模糊函数最大值函数：

(15)

则可以用MMX(p)表示不同有限域GF(p)信号集Sp互时延模糊函数的性能变化。

2.3 信号集大小与序列长度

对于给定的素数p，有限域GF(p)的信号集大小|Sp|=φ(p-1)。对于安全素数p=2p1+1，则有

|Sp|=φ(2p1)=p1-1.

(16)

信号集大小依赖于素数p，而素数的选择又与时间带宽积所允许的序列长度N有关。

已知序列长度N通常有两种选择[20]：一种是最小化时延自模糊函数旁瓣的选择，为

(17)

式中：B为信号总带宽；ka为序列自相关旁瓣最大值。另一种称作奈奎斯特选择，为

(18)

与最小化时延自模糊函数旁瓣的选择相比，奈奎斯特选择下信号时延自模糊函数的旁瓣值稍高，但时延自模糊函数拥有更陡峭的中心区域。

在信号时间带宽积一定时，序列长度N的选择就决定了信号时频变化在时频平面的精细程度。奈奎斯特选择下信号子脉冲的时间带宽积TsBs≈1，信号子脉冲已经是不可压缩信号，因此奈奎斯特选择实际是序列长度N的上限值。

3 仿真实验

假定信号集的总带宽为1 000 Hz，起始频率为500 Hz，信号时长1 s，采样率为10 kHz. 通过2.1节所述的Costas序列生成方法，对p<1 000的素数进行仿真分析。以p=107为例，X107中α=2对应W1序列的自时延差异函数如图3所示，X107中α=2与α=5对应W1序列的互时延差异函数如图4所示。由图3和图4可以看出，序列的自时延差异函数具有尖锐的主瓣，互时延差异函数在整个时间范围内具有很低的相关峰。

图5 S107中α=2与α=5对应的Costas编码跳频信号时域波形和信号频谱Fig.5 Waveforms and spectra of signals related to α=2 and α=5 in S107

图3 X107中α=2对应W1序列的自时延差异函数Fig.3 Self-difference function of W1 related to α=2 in X107 in time field

图4 X107中α=2与α=5对应W1序列的互时延差异函数Fig.4 Cross-difference function of W1 related to α=2 and α=5 in X107 in time field

对比本文方法和OFD-LFM方法生成的正交信号集，同样以p=107为例，S107中α=2与α=5对应的Costas编码跳频信号时域波形和信号频谱如图5所示。由图5可以看出，两个编码信号在不同子脉冲区间的频率不同，二者在频域内不同频点的能量大小也不同，但两个信号带宽都为1 000 Hz，利用了系统的全部带宽。图6所示为具有同样系统带宽和信号集大小的OFD-LFM信号，但每个信号带宽仅有19.2 Hz，与Costas信号相比，所能获取的时间增益较小。α=2对应编码信号的自模糊函数如图7所示，α=2与α=5对应编码信号的互模糊函数如图8所示。从图7和图8中可以看出，Costas编码的跳频信号具有图钉状的自模糊函数，同组正交编码跳频信号集中不同信号间具有近似理想的正交性。

图6 OFD-LFM信号集中信号s0与信号s1的时域波形和信号频谱Fig.6 Waveforms and spectra of s0 and s1 in OFD-LFM set

图7 S107中α=2对应编码跳频信号的自模糊函数Fig.7 Self-ambiguity function of signal related to α=2 in S107

图8 S107中α=2与α=5对应编码跳频信号的互模糊函数Fig.8 Cross-ambiguity function of signals related to α=2 and α=5 in S107

从图9中可以看出，相比于全体素数，形如p=2p1+1安全素数的有限域GF(p)，其所生成的序列集和信号集具有更加优良的正交性能；从图10中可以看出，安全素数的信号集大小与该素数的比值形成了图中斜率最大的直线。因此，在选择序列长度N时，无论从信号集正交性角度考虑还是从信号集的大小考虑，选择p=2p1+1形式的安全素数都是最优的。

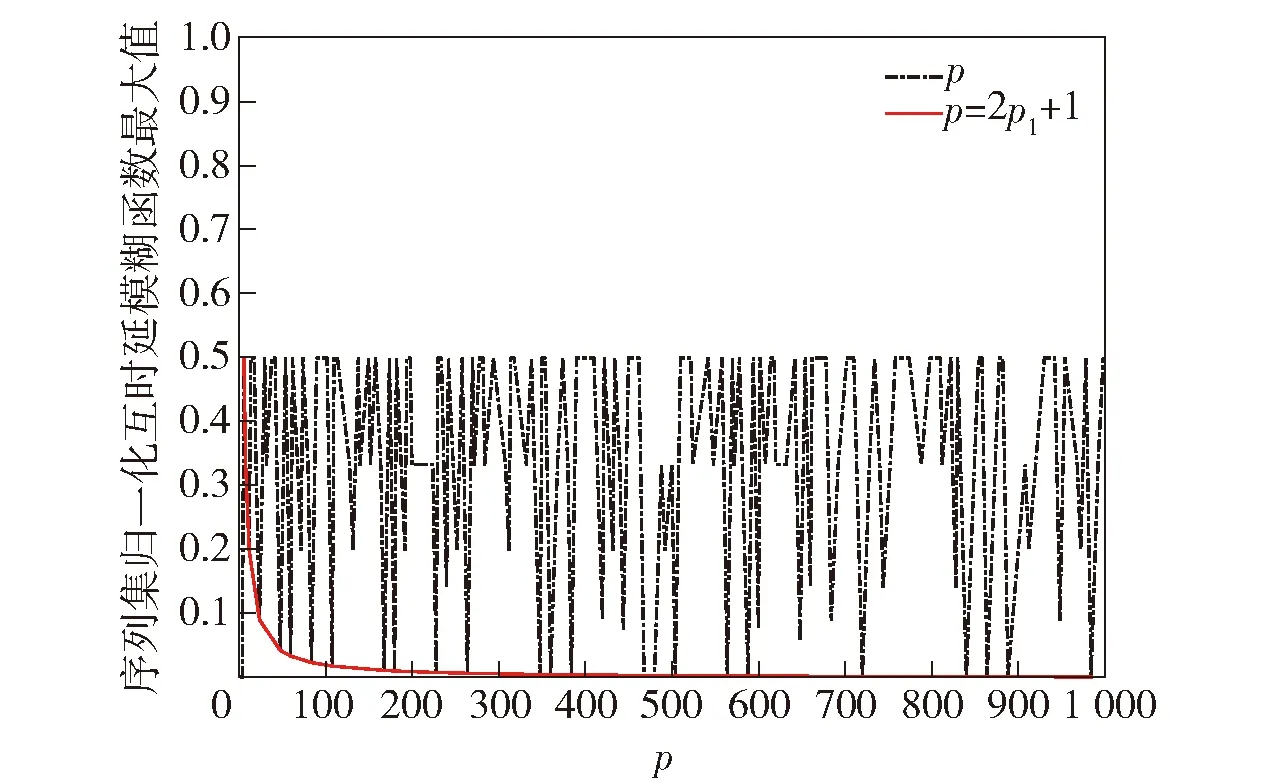
图9 不同GF(p)序列集的互时延模糊函数最大值变化曲线Fig.9 Maximun changing curves of MMC(p)

图10 信号集大小|Sp|随素数p的变化曲线Fig.10 |Sp| vs. p

跳频信号集的正交性与序列集密切相关，如图11所示，其中，图11(a)表示X107时延差异函数图谱，图11(b)表示带宽B=1 kHz和信号时长T=1 s时S107的时延模糊函数图谱。从图11、图12的对比中可以再次验证：安全素数所对应的有限域能够生成具有优异正交性的跳频信号集。

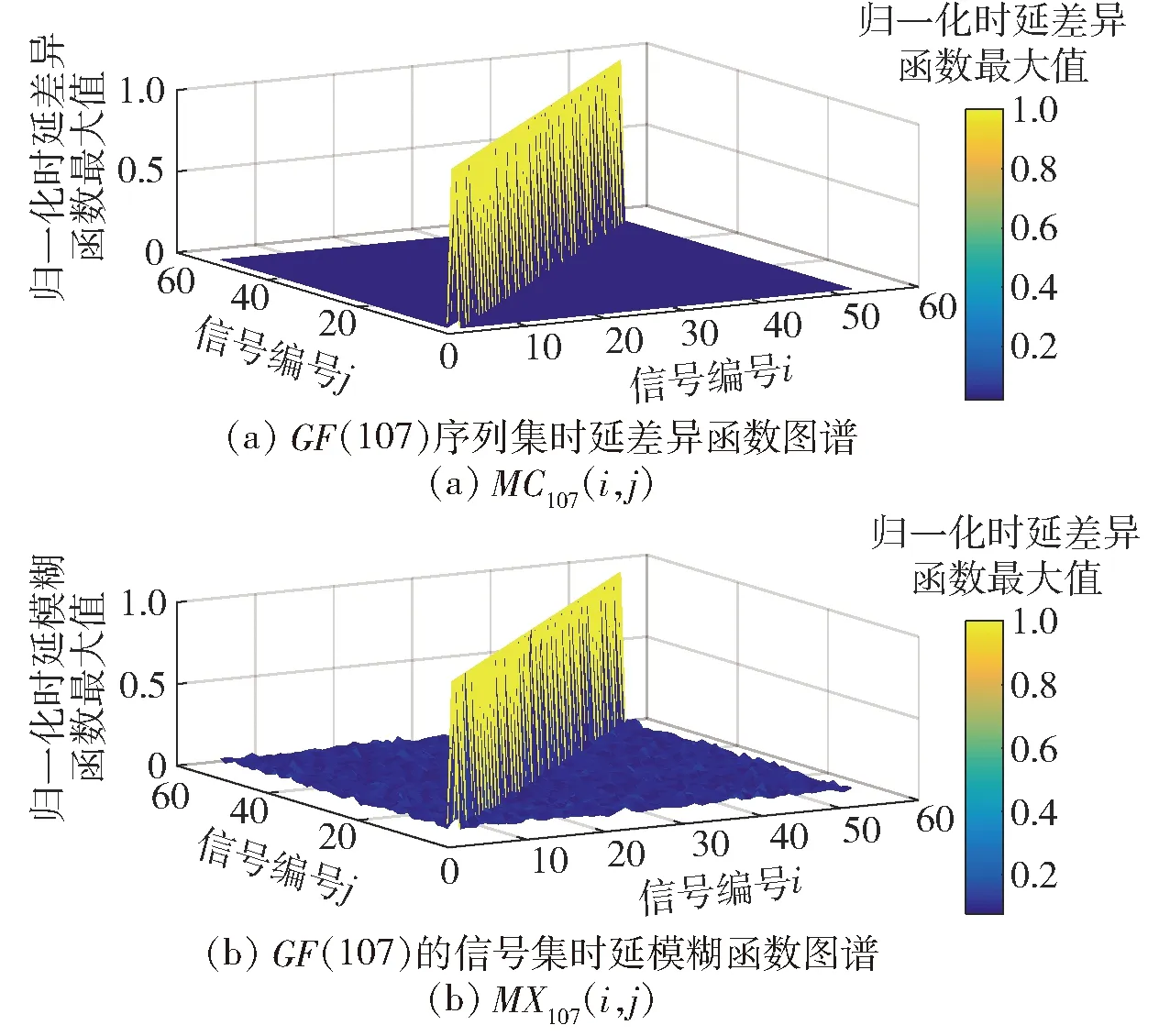
图11 GF(107)序列集和信号集的正交性Fig.11 MC107(i,j) and MX107(i,j)

图12 GF(113)序列集和信号集的正交性Fig.12 MC113(i,j) and MX113(i,j)

图13 GF(p)的信号集归一化互时延模糊函数最大值曲线Fig.13 MMX(p) for B=1 kHz, T=1 s and B=0.75 kHz, T=2 s

再次设定信号集总带宽为750 Hz，起始频率500 Hz，信号时长2 s，采样率10 kHz，与前述仿真条件下的信号集性能进行对比。如图13所示，对于全体素数，当时间带宽积BT不同时，信号集正交性较差的素数p出现的位置不同，但对于安全素数，对应生成的信号集能始终保持良好的正交性。

4 结论

为满足MIMO声纳对发射信号集的正交性需求，本文提出了一种基于Costas序列的MIMO声纳正交发射信号集设计方法。针对常规宽带信号在工作带宽限制下单个信号带宽与发射信号集大小相互制约的矛盾，利用安全素数生成的Costas序列编码跳频信号有效解决了该问题，并通过仿真实验进行了验证。仿真结果表明，对于1 000以内的素数，基于安全素数的有限域构造的正交跳频信号集不仅具有最优的正交性，还能取得最大的信号集大小。