巧用三角板教学平行四边形的性质

王彩霞

关键词：三角板;教学;平行四边形;性质

【中图分类号】G623.5    【文献标识码】A       【文章编号】1005-8877（2019）22-0014-02

平行四边形是一种基本的几何图形，在我们的生活中随处可见，如庭院的篱笆门，小区的伸缩门，载重汽车的护栏等等。《数学课程标准》指出，“有效的数学学习活动不能单纯的依赖模仿和记忆，动手实践、自主探索和合作交流是学生学习数学的重要方式”。因此，关于平行四边形性质的教学，笔者在学生的认知发展水平和已有知识经验的基础上，用数形结合的方法，利用身边常用的教学工具“三角板”进行讲解。这样做，激发了学生动手操作的积极性，向学生提供了充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、思想和方法，获得广泛的数学活动经验，取得良好的教学效果。这节课笔者是这样讲解的。

1.导入

提问：在生活中，有哪些具有平行四边形形状的物体？

生1：窗户的防盗栏

生2：花园的栅栏

生3：伸缩衣架

生4：消防云梯

生5：折叠椅

我拿出准备好的两个全等的直角三角板拼图。先用两个全等的三角板拼出平行四边形，如图1。

提问：我手中拼出的图形是什么？

学生集体回答：平行四边形

追问：你们怎么知道它是平行四边形？

学生回答：看到的呀！

看到的就是真的吗？这节课我们一起来探究，看看你看到的图形是不是平行四边形。

2.新知探究

探究一：拼图是不是平行四边形？它的对边有什么关系？

师：两组对边分别平行的四边形是平心四边形。你看到的这个用三角板拼成的四边形是不是平行四边形？小组合作，用全等的两个三角板拼接出同样的图形，观察探究，找出两组对边的位置关系。

学生交流：

生1：这个拼图是平行四边形。因为图1四边形ABCD中，∠ADB=∠CBD=30度;∠ABD=∠CDB=90度;所以 AD// BC，AB//DC，两组对边分别平行。

生2：我发现这个拼接的平行四边形的两组对边分别相等。图1中，平行四边形是由两个全等的直角三角形板拼接而成，所以对边相等。

师：观察，这个平行四边形的对角有什么关系？

生1：平行四边形的对角相等。

追问：怎么知道平行四边形的对角相等？

生2：图1中，平行四边形是由两个全等的直角三角形拼接而成的，其中一组对角是全等三角形的对应角，是相等的。另一组对角都是三十度角与九十度角的和，所以也相等。

探究二：师：请各小组用四个全等的直角三角板拼接一个平行四边形，如图2，仔细观察对角线的关系。

交流：平行四边形的对角线互相平分。

提问：你能说说对角线互相平分的理由吗？

生：因为四个直角三角板是全等的，它们的对应边相等，所以这个平行四边形的对角线也就互相平分。

探究三：师：以上我们是用直角三角板拼接成的平行四边形，它们是特殊的平行四边形。那么一般的平行四边形是否也是由两个全等的任意三角形组成，且满足这些性质呢？请大家在练习本上画出一个任意平行四边形ABCD。

求证：

（1）这个平行四边形由两个全等三角形组成。

（2）对边平行且相等。

（3）对角相等。

（4）对角线互相平分。

证明：1.连接AC

∵AD// BC，AB//DC

∴∠DAC=∠BCA ，∠BAC=∠DCA（两直线平行，内错角相等。）

在△ABC和△CDA中

∵ ∠DAC=∠ACB

AC=CA

∠BAC=∠DCA

∴△ABC≌△CDA   （SAS）

∴AD=BC.AB=DC（全等三角形的对应边相等）

∠ABC=∠CDA.同理∠BAD=∠DCB

即平行四边形的两组对边平行且相等，对角相等。

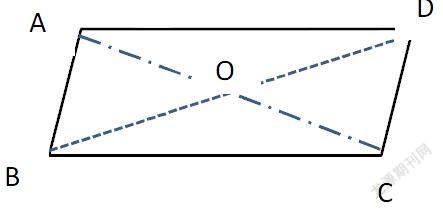
证明3：连接BD交AC于点O

∵四边形ABCD是平行四边形

∴AD=BC.AD‖BC.

∴∠DAO=∠BCO，∠ADO=∠CBO（两直线平行，内错角相等）

在△AOD和△COB中

∠DAO=∠ACB

AD=BC

∠ADO=∠DBC

∴△AOD≌△COB   （ASA）

∴OA=OC.OB=OD

即平行四边形的对角线互相平分。

3.当堂练习

在平行四边形ABCD 中 BC=10，AC=8，BD=14，AC、.BD相较于点O。求△AOD的周长是多少？△ABC与△DBC的周长哪个长？长多少？

先让学生读图，读题，思考，在进行讨论，最后分别叫学生在黑板上讲解做题思路并书写做题过程。等学生做完我再对做题过程进行纠正。

4.反思

这节课中，我们用身边现有的三角板拼接成平行四边形，图形看起来形象直观，所有的性质在图像中都可以呈现出来。但常用的三角板都是直角三角形，具有特殊性。在特殊三角形拼接成平行四边形的基础上，学生自然能联想到任意三角形拼接成的平行四边形，其性質一样明显。由此得出这样的结论：任何一个平行四边形中的每一条对角线都可以把平行四边形分割成两个全等的三角形。也就是说，任何一个平行四边形都可以看作是由一对全等三角形拼成的。可见，用三角板学习平行四边形的性质，虽然具有特殊性，但与普遍规律并不矛盾。笔者认为，用三角板巧解平行四边形的性质的方法，一方面激发了学生学习的积极性，另一方面学生学起来通俗易懂，易于接受和理解。

参考文献

[1]陈江嵩.关于“三角板中的数学问题”教学设计和思考[J].考试周刊，2014（73）：67+83