罗德里格矩阵在盾构姿态解算中的应用

魏云豹 刘恒杰 周小利

摘 要：在大量實际隧道工程中，采用罗德里格矩阵进行盾构机轴线精确解算，其精度可达到毫米级，完全可满足日常隧道施工需求。由此，本文介绍了利用罗德里格矩阵模型和反对称矩阵，把传统七参数模型中的三个旋转参数用反对称矩阵中三个独立参数代替，使用Excel表格工具解算出盾构机轴线坐标。

关键词：盾构机轴线坐标;罗德里格矩阵;三维坐标转换

中图分类号：U452.13 文献标识码：A 文章编号：1003-5168（2019）28-0076-04

Application of Rodrigue's Matrix in Attitude Calculation of Shield Machine

WEI Yunbao LIU Hengjie ZHOU Xiaoli

（China Railway Engineering Equipment Co.， Ltd.，Zhengzhou Henan 450000）

Abstract： In a large number of practical tunnel projects， Rodrigo's matrix is used to accurately calculate the axis of shield machine， and its accuracy can reach millimeter level， which can fully meet the needs of daily tunnel construction. Therefore， this paper introduced using Rodrigo's matrix model and antisymmetric matrix， replacing three rotation parameters in the traditional seven parameter model with three independent parameters in antisymmetric matrix， and using Excel table tool to solve the axis coordinates of shield machine.

Keywords： shield machine axis coordinate;Rodrigo's matrix;3-D coordinate conversion

盾构机是一种被广泛应用于城市地铁建设的大型工程机械。精确计算盾构机轴线坐标精度是保证其正常掘进的关键。本文主要以罗德里格矩阵计算盾构机轴线精度。

1 数学模型

零位坐标系中，盾构机的轴线坐标和特征点坐标是已知的。在施工过程中，当地坐标系下的特征点坐标是可以通过全站仪实测得到的，这样就可以通过公共特征点建立2个坐标系的空间关系式，即求解7参数，包括3个平移参数、3个旋转参数、1个尺度参数（[Δx]、[Δy]、[Δz]、[θ1]、[θ2]、[θ3]、[K]），进而解算出盾构机的轴线坐标[1-4]。

根据坐标转换的物理过程，可得到如式（1）所示的数学模型：

[xyzi=kΔxΔyΔz+kRxyzI]                （1）

根据罗德里格矩阵原理，具有3个自由度的正交旋转矩阵[R]可以看成是由反对称矩阵[S]构成的罗德里格矩阵：

[R=I+SI-S-1]                     （2）

[S=0-c-bc0-aba0]                            （3）

式中，[a]、[b]、[c]是3个未知参数，用于替代3个旋转参数，简化计算过程，由式（1）可知2个公共点可以列6个方程式。

在7个参数模型中，[R]为3个旋转矩阵的乘积：

[R=RxαRyβRzγ=1000cosαsinα0-sinαcosαcosβ0-sinβ010sinβ0cosβcosγsinγ0-sinγ-cosγ0001]           （4）

空间中有两个不同的坐标系，即零位坐标系[Oi-xyzxiyizi]和当地坐标系[OI-xyzxIyIzI]，同时有[n]个公共点[i，I=1，2，3，…]。

由于在实际盾构机轴线坐标解算中尺度变换为零，故[k=1]，这样只需要解算出旋转参数和平移参数即可。

旋转参数解算：将公共点[ni]与[nI]在[Oi-xyzxiyizi]和[OI-xyzxIyIzI]中的坐标值带入（1）式得：

[xi'yi'zi'=kΔxΔyΔz+kRxiyizi]                    （5）

[xI'yI'zI'=kΔxΔyΔz+kRxIyIzI]                     （6）

将式（5）和式（6）相减，消去平移参数，整理后可得：

[xI'-xi'yI'-yi'zI'-zi'=kRxI-xiyI-yizI-zi]                         （7）

将式（2）与式（7）结合，整理后为：

[0-zIi-zIi'-yIi-yIi'-zIi-zIi'0xIi+xIi'yIi+yIi'xIi+xIi'0abc=xIi'-xIiyIi'-yIizIi'-zIi]            （8）

由于式（8）的系数阵为反对称矩阵，行列式为0，秩等于2，式（8）中只有两个独立方程，无法解出3个参数[a]、[b]、[c]，因此需要将3个公共点[n1]、[n2]、[n3]代入式（1），按照同样原理与式（8）联合解出未知参数[a]、[b]、[c]，方程组如下：

[0-z21-z21'-y21-y21'-z21-z21'0z21+z21'y21+y21'x21+x21'00-z31-z31'-y31-y31'-z31-z31'0z31+z31'y31+y31'x31+x31'0abc=x21'-x21y21'-y21z21'-z21x31'-x31y31'-y31z31'-z31]        （9）

根据式（9）即可解出未知参数[a]、[b]、[c]，再结合式（2）可解出旋转矩阵[R]。

平移参数计算：根据上述公式解出旋转矩阵[R]，代入式（1），即可解出平移参数[Δx]、[Δy]、[Δz]。同理，求出每个点的平移参数，再计算平均值。

2 计算步骤

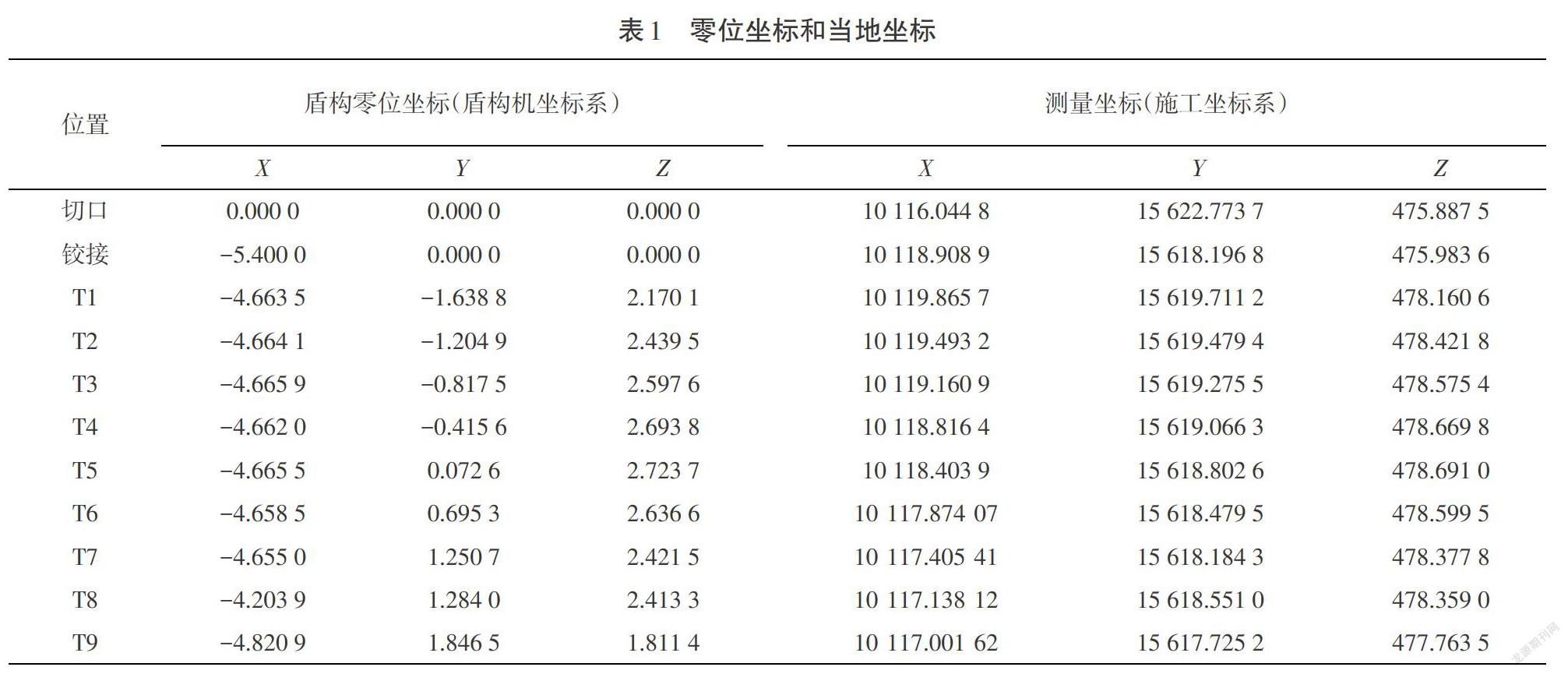
第一步：把零位坐标系和当地坐标系下的公共点（特征点）输入表1中。

第二步：根据式（9）列出矩阵列表，如表2所示。

第三步：用Excel中的TRANSPOSE命令算出[B]矩阵的转置矩阵[BT]。首先在Excel中确定矩阵[B]的范围（列数和行数），然后在空白区域选择矩阵[B]的行数和列数，然后在选定范围后输入转置矩阵函数，例如：选中范围后输入函数=TANSPOSE（B2：D19），然后按Ctrl+Shift+Enter键，即可求出转置矩阵[BT]。

第四步：用Excel中的MMULT命令算出[BTB]。首先在Excel表确定乘积矩阵的行数和列数范围。然后在输入栏中输入矩阵乘积函数，例如，=Mmult（F4：W6，B2：D19），然后按Ctrl+Shift+Enter键，得出[BTB]。

第五步：用Excel中的MMULT命令算出[BTL]。

第六步：用Excel中的MINVERSE命令算出[（BTB）-1]。

第七步：用Excel中的MMULT命令求转换参数[a]、[b]、[c]。

[abc=（BTB）（BTB）-1]                           （10）

第八步：根据式（1）算出每个点的平移参数[Dx]、[Δy]、[Δz]后取平均值。

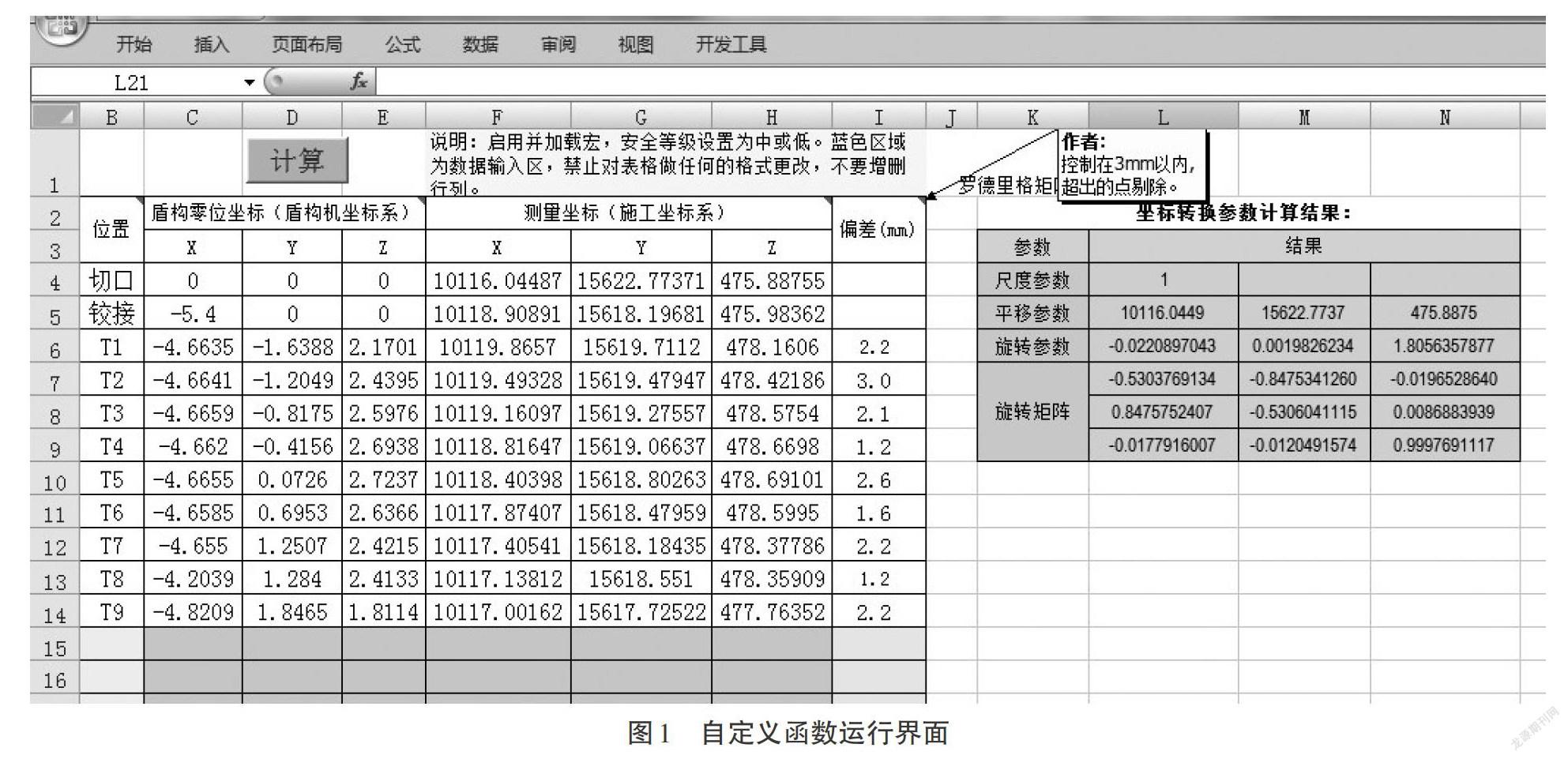
运行界面见图1。

3 工程应用验算

本算例中，盾构机轴线坐标和特征点坐标为现场实际坐标;零位坐标系为任意设站转换为机器坐标系（盾构机盾首坐标[x=0]、[y=0]、[z=0]，盾尾坐标[x=-5.4]、[y=0]、[z=0]）;施工坐标系为当地坐标系。

3.1 模型建立

零位坐标系下的坐标，按CAD法整体转换到当地坐标系中，然后提取各特征点坐标和盾构机轴线坐标，特征点和盾构机轴线坐标相对空间关系固定有唯一解。

3.2 验算过程

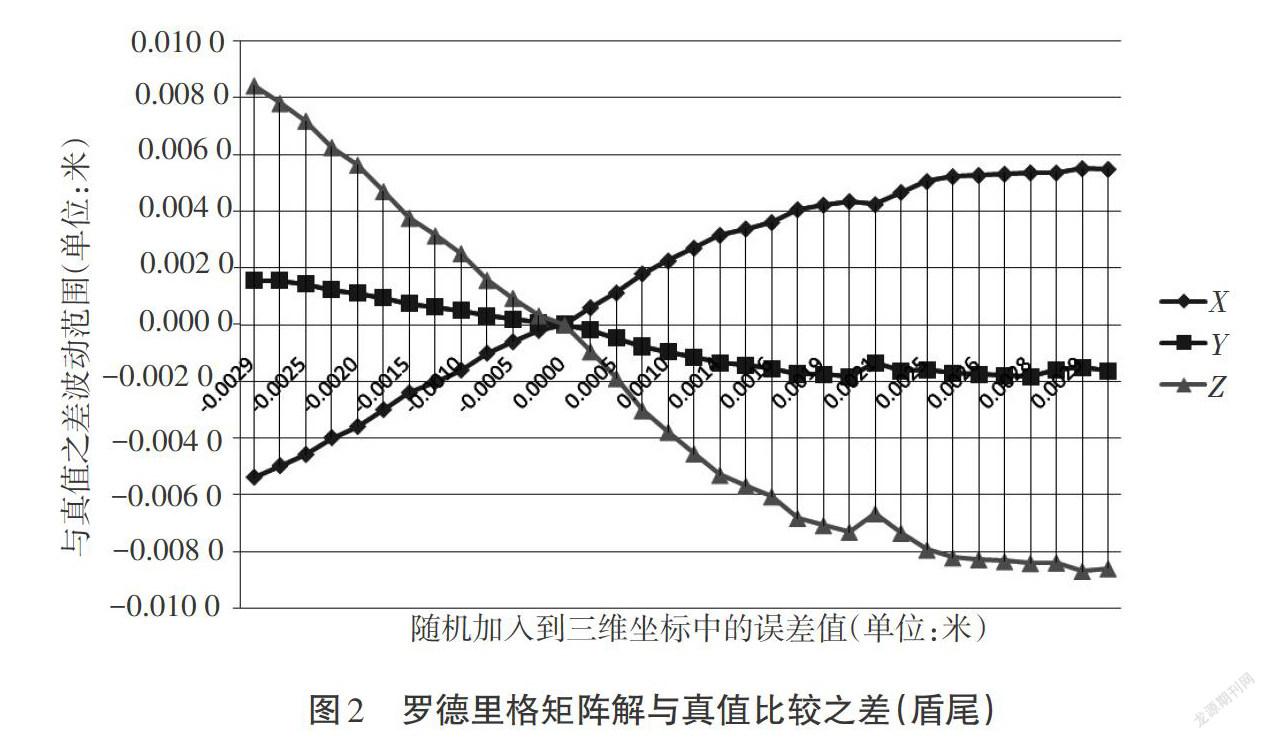
随机在当地坐标系（[x]，[y]，[z]）下加入-0.003～0.003m的误差（实际工作中，误差不能超过0.003m限值）;图2为罗德里格矩阵解与真值比较之差（盾尾），图3为罗德里格矩阵解与真值比较之差（盾首），数据采集为69组。通过分析可知在限差范围-0.003～0.003m内，盾尾各坐标（[x]，[y]，[z]）波动都在-0.004 7～0.004 8m，盾首各坐标（[x]，[y]，[z]）波动都在-0.004 7～0.004 8m，可满足日常施工要求。

4 结语

在大量实际隧道工程中，采用罗德里格矩阵进行盾构机轴线精确解算，其精度可达到毫米级，完全可满足日常隧道施工需求（隧道施工测量要求为公分级）。同时，把罗德里格矩阵解算过程通过Excel表格形式逐步展示出来，可以为其他研究人员提供良好的参考价值。

参考文献：

[1]姚吉利，韩保民，杨元喜.罗德里格矩阵在三维坐标转换严密解算中的应用[J].武汉大学学报（信息科学版），2006（12）：63-65，88.

[2]潘国荣，周跃寅.两种坐标系转换计算方法的比较[J].大地测量与地球动力学，2011（3）：62-66.

[3]潘国荣，汪大超，周跃寅.两种大转角空间坐标转换模型研究[J].山东科技大学学报（自然科学版），2015（1）：61-67.

[4]原玉磊，蒋理兴，刘灵杰.罗德里格矩阵在坐标系转换中的应用[J].測绘科学，2010（2）：178-179.