巧用“整体法”求解高中物理难题

陈建发

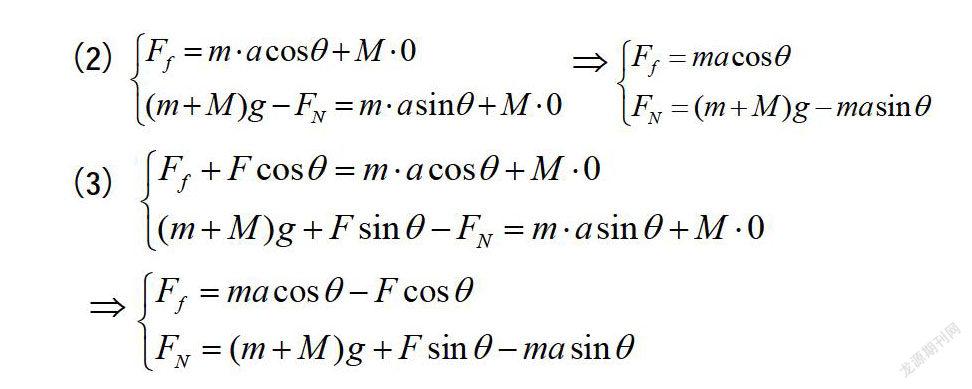
摘  要：整体法是对整个系统或整个过程进行分析的研究方法。整体法是从局部到全局的思维过程，是系统论中的整体原理在物理中的应用，它以系统为研究对象，以全过程为研究过程，从全局的视角揭示物理现象的本质规律。运用整体思维分析问题，可以避开中间量的求解，避繁就简，化难为易，是多种思维的融会贯通，更是知识体系的重新构建。笔者根据多年教学经验，对“整体法”解决“多个对象”“多个过程”以及“多个未知量”等问题，进行初步探讨。

关键词：整体法;多个对象;多个过程;多个未知量

一、巧用“整体法”求解“多个对象”问题

对多个物体组成的系统，牛顿第二定律可以表述为：系统受到的合外力等于系统内各部分质量与相应加速度乘积的矢量和，即或者系统的牛顿第二定律表达式左边只有系统外力，因此它只适用于处理系统外力相关问题，一旦涉及系统内力，则只能用隔离法;表达式右边为系统内各部分质量乘以相应的加速度，然后矢量相加。因此并不要求各部分相对静止，各部分间有相对速度、相对加速度时，仍然可以选系统为研究对象，使用整体法处理问题。另外，表达式右边各部分相应的加速度可能有些为零，有些不为零，但这并不影响等式严谨性。

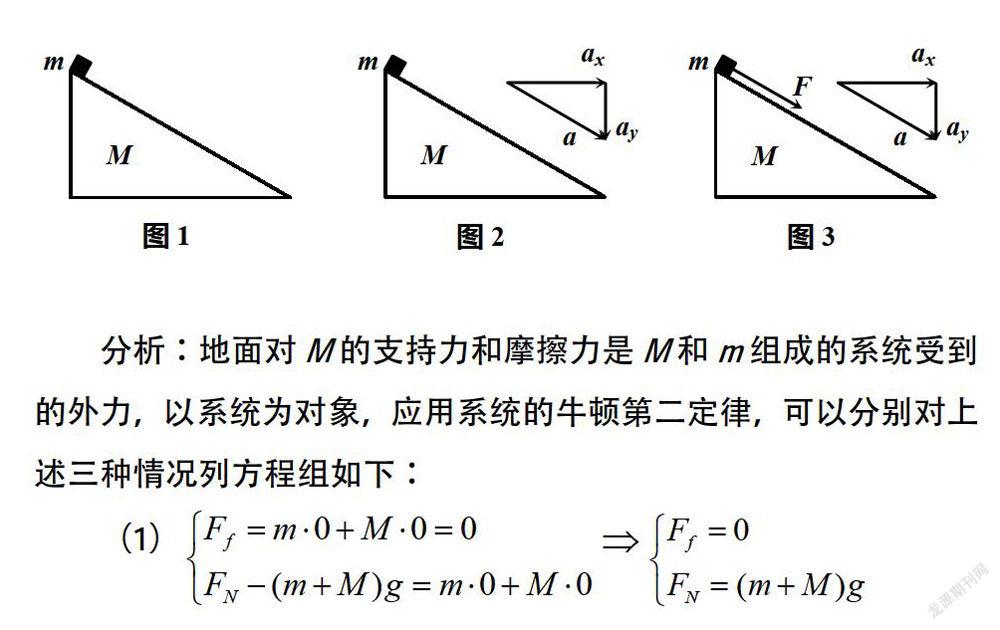
例1：如图所示，倾斜角为θ的斜面体M始终静止在水平地面上，求不同情况下，地面对M的支持力FN和摩擦力Ff的大小：（1）m在斜面体上处于静止;（2）m沿斜面以加速度a加速下滑;（3）m在平行斜面向下的拉力F作用下，沿斜面以加速度a加速下滑。

分析：地面对M的支持力和摩擦力是M和m组成的系统受到的外力，以系统为对象，应用系统的牛顿第二定律，可以分别对上述三种情况列方程组如下：

上述分析选系统为对象，用整体法沿水平和竖直两个垂直方向列方程组，可快速解出地面对斜面体施加的两个外力。最后的结论也不难理解，比如：第（2）种情况下，m有竖直向下的加速度，就处于失重状态，来自地面的支持力等于系统的重力之和扣掉因m失重而少掉的部分，而来自地面的摩擦力使系统内的m获得向右的加速度，故摩擦力的方向也向右。学生容易产生较大疑问的是：为什么作用在M上的力却使m获得加速度？事实上，系统的牛顿第二定律是把系统内各部分受到的内力、外力全部相加进而推导出来的。其中成对出现且等值反向的内力总和为零，等式的一边只剩下外力的矢量和。但是，内力对系统内特定的一部分还是起作用的，比如上述中的M对m的作用力会对m运动状态产生影响，因此，来自地面的摩擦力正是通过斜面体间接使m获得水平加速度。

上述第（3）种情况下得出的摩擦力表达式中出现两式相减，在两项大小关系不确定的情况下，摩擦力可能向左、向右或为零，考虑到结论的严谨性，摩擦力的大小可以表述为：

二、巧用“整体法”求解“多个过程”问题

高中物理习題中涉及多过程问题的不胜枚举，但这类问题的重要考点往往只关心初末状态或初末位置各个物理量的变化情况，解题时可以避开繁琐的中间环节，直接列方程求解。高中阶段相关的重要考点包括：保守力做功，动能定理，机械能守恒定律，能量的转化与守恒，动量守恒定律等。

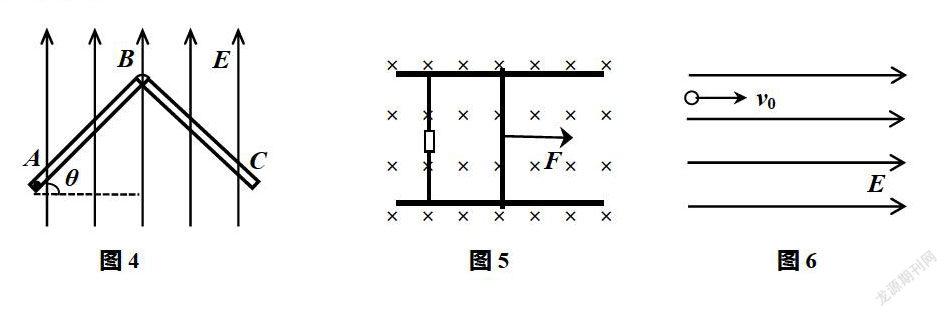
例2：如图4所示，一根对称的“Λ”形玻璃管放置于竖直平面内，管AB和BC长均为L，与水平方向的夹角均为θ，空间有一竖直向上的匀强电场E，有一个质量为m，电量为+q的小球在管内从A点由静止开始运动，它与管壁的摩擦系数为μ，小球在B端与管作用时无能量损失，设qE>mg，μ

分析：小球在“Λ”形玻璃管内往复运动若干次后，最终静止在B端，由于重力和电场力做功与路径无关，而摩擦力始终做负功，且摩擦力大小保持不变，取多个往复过程为一个研究整体，从初位置至末位置，根据动能定理有

式中s即为所求。此题如果不避开繁琐的中间过程，将变的很难求解。

三、巧用“整体法”求解“多个未知量”问题

高中物理习题中有一类题目通过巧妙设问，使得题目中的一些物理量不得不视为一个整体才能方便解题。比如复杂电路问题，多种形式能量的转化与守恒问题等，这类题目难度较大，解题时选择合适的多个物理量作为“整体”显得尤为关键。

例3：如图5所示，水平面上两根足够长的光滑金属导轨平行固定放置，一端通过导线与阻值为R=0.5Ω的电阻连接，一电阻r=0.3Ω，质量m=0.1kg的金属杆垂直导轨放置，保持跟导轨良好接触;匀强磁场竖直向下，分布范围足够大;现用与导轨平行的恒力F向右拉金属杆，杆最终以v=2m/s匀速运动，这时流过金属杆的电流为I=2A。求：（1）恒力F的大小;（2）从撤去恒力F，到金属杆最终停下，通过金属杆的电量q。

分析：（1）杆匀速运动时受力平衡，恒力F与安培力相等，即：或。显然两个式子都因存在“B”和“L”两个未知量导致未能得出结论。而利用上述等式容易先求出两个未知量的乘积“BL”，然后将其反代回原来的式子就可以顺利求出恒力F。

（2）撤去恒力F后，金属杆在安培力作用下最终停止运动，这一过程通过金属杆的电量：，而根据动量定理有：。两式联立即可求出电量q。但不难看出“BL”再次作为一个整体出现在式中，且“”也是两个未知量以整体形势出现。这种情况下，要单独求出其中一个量是很困难的，或者是求不了的。

例4：如图6所示，将一带负电的小球向右水平抛入范围足够大的匀强电场，电场方向水平向右，不计空气阻力，则小球在电场中（ ）

A.机械能一直增大

B.机械能一直减小

C.小球的动能和电势能总和一直增大

D.小球的动能和电势能总和一直减小

分析：小球运动中有重力势能、动能和电势能等三种能量参与转化，但总能量守恒。解题时抓住“守恒”之根本，当把重力势能和动能视为整体（即机械能）时，其变化情况刚好与电势能变化情况相反;而把动能和电势能视为整体时，其变化情况刚好与重力势能的变化情况相反。这样，通过分别判断重力势能和电势能的变化情况，就能快速得出正确答案。本题如果改编为更多形式的能量参与变化，并把定性判断变为定量计算，难度就变大了。但只要抓住“总能量守恒”这一关键，选择合适的几种能量作为整体，研究剩余能量的变化情况，便能使一道难题转变为简单的物理问题。

综述：整体法强调充分运用整体思维，以全局的视角，从整体或全过程去把握物理现象的本质和规律。运用整体法可以把具有相互联系、相互依赖、相互制约、相互作用的多个物体、多个状态，或者多个物理变化过程组合作为一个融合加以研究，也可以是把多个具有制约关系的物理变量作为一个变量加以研究，是一种综合的思维方法。其优点是只须分析整体与外界的关系，避开了整体内部繁杂制约关系和变化过程，能更便捷、更巧妙地展现出物理量间的关系。整体法是一种解决高中物理难题的重要思想方法。

参考文献：

[1]赖丰亮——试析高中物理力学解题中对整体法的运用，《中学物理》，2015;

[2]龚竞秋——浅议高中物理力学解题中整体法的运用，《新课程》，2013;

[3]黎国胜——高中物理“整体法与隔离法”的教学难点及突破，《基础教育参考》，2012。