基于传递系数法的隧道洞口顺层仰坡加固稳定性评价

刘伟

摘 要：顺层岩体仰坡地形、地质条件复杂。为预防工程事故，需要运用预应力锚索对隧道洞口仰坡进行加固。结合宝汉高速石门隧道洞口仰坡的研究，在传递系数法理论支撑下，结合理正分析软件分析仰坡加锚的必要性，通过锚固加固计算理论得出仰坡的加固方案，运用MIDAS数值模拟软件对加锚后的顺层仰坡进行模拟分析。结果表明：锚索加固后，仰坡坡顶位移速率未超过规范规定的位移速率限值。同时，结合仰坡稳定安全系数的分析得出，稳定安全系数大于规范规定的限值，充分证明了仰坡的稳定性。

关键词：传递系数法;顺层仰坡;位移速率;稳定安全系数

中图分类号：U458 文献标识码：A 文章编号：1003-5168（2019）34-0103-06

Stability Evaluation of Tunnel Portal Reinforcement along the

Front Slope Based on Transfer Coefficient Method

LIU Wei

（China Traffic Tongli Shaanxi Environmental Greening Engineering Co.， Ltd.，Xi’an Shaanxi 710075）

Abstract： The topography and geological conditions of the bedding rock mass slope are complex. To prevent engineering accidents， prestressed anchor cables are needed to reinforce the tunnel entrance slope. The research on the slope of the Baomen Tunnel’s entrance in Baohan Highway was carried out. Under the theory support of transfer coefficient method， and combined with the Lizheng analysis software to analyze the necessity of anchoring the slope， the reinforcement scheme of the slope was obtained by the calculation theory of anchoring reinforcement. The numerical simulation software MIDAS simulated the bedding slope after anchoring. The results show that strengthened by anchor cables， the displacement rate of the bedding slope’s top does not exceed the displacement rate limit by the specification， combined with the stability safety factor analysis of the slope， the stability safety factor is greater than the limit specified in the code， which fully proves the stability of the slope.

Keywords： transfer coefficient method;bedding slope;displacement rate;stability safety factor

隧道洞口段一般埋深較浅、岩体破碎、风化剧烈、稳定性差。若洞口仰坡倾角与岩层倾角较为接近时，将形成顺层仰坡的特殊地质构造，在施工中易受扰动后失稳，出现结构崩塌、顺层滑坡等工程事故，严重威胁施工安全[1]。因此，对隧道洞口的顺层仰坡稳定性进行分析，并对其进行有效加固具有重大工程意义。

目前，有的学者主要利用传递系数法中的隐式解进行顺层仰坡的稳定性分析[2];还有学者将传递系数法作为边坡主被动锚固方法中稳定安全性判别的主要方法[3]。但是，这些理论研究均未考虑隧道开挖对仰坡的稳定性的影响。

因此，通过研究边坡锚固理论，利用传递系数法得出仰坡的加固设计方案，结合理正有限元分析软件（基于传递系数法）的抗滑桩模块，分析自然状态下仰坡稳定性，得知仰坡安全系数低于规范规定的限值，安全性较低，必须进行加固。然后利用MIDAS有限元分析软件进一步分析隧道开挖的仰坡稳定性。结果证明，仰坡处于稳定状态。此结论为进一步研究仰坡稳定性提供了参考。

1 传递系数法仰坡加固机理

在仰坡加固分析中，极限平衡法和强度折减法是目前国内外工程中最常用的方法。其中，极限平衡法按滑移面形式的不同又分为单平面滑移面法、圆弧滑移面法（简化Bishop法）、折线滑移面法（Sarma法）、任意滑移面法（传递系数法）[4]。传递系数法最简便且精度较高，故本文选其作为分析计算的方法。

运用传递系数法进行分析计算时，将滑动土体竖直分成若干个土条，把土条看成是刚体，考虑条块间的相互作用力，并假定条块剩余下滑力平行于该条块滑面，然后分别求出作用于各个土条的滑动力矩和抗滑力矩，进而得出边坡稳定性系数及剩余下滑推力[5-7]。

传递系数法也称作剩余下滑力法，其是目前广泛采用的一种边坡稳定性分析方法。传递系数法主要分为隐式解法和显式解法。大量工程实践及滑坡稳定性计算证明，显式解法不适用于滑坡稳定性分析[7]。因此，本文采用传递系数法的隐式解法来进行仰坡稳定性分析。

2 基于传递系数法的预应力锚索加固设计

锚索是若干股钢绞线固定于钢锭内，其一端作为锚固段注浆并插入稳定基岩中，另一端为锚头段固定在仰坡坡面上。预应力锚索的作用机理是：通过预拉锚索，对滑移面产生挤压作用，从而达到限制位移、防止滑移的目的。

2.1 预应力锚索锚固力计算

假设顺层仰坡中设置了[n]排间距相同的预应力锚索，其中锚索间距为[Pt]，每束锚索的锚固力为[Pt]，锚固倾角为[θi]，潜在滑移面倾角为[αi]，仰坡加锚图如图1所示[8]。

第[Pi]排预应力锚索产生的单位宽度的抗滑力[Pi]为：

[Pi=1aPt[cos（αi+θi）+sin（αi+θi）tanφi]]       （1）

总抗滑力为：

[Pt=i=1nPi=Pta·i=1ncos（αi+θi）+sin（αi+θi）tanφi] （2）

为了使锚固后的仰坡达到稳定，则令：

[P=E]                                    （3）

将式（3）代入式（2）得：

[ξi=cos（αi+θi）+sin（αi+θi）tanφi]                 （4）

式中，[ξi]为锚固预应力系数;[φi]为第[i]排预应力锚索穿过的滑移面内摩擦角。

2.2 锚索极限抗拔力的计算

锚固段的注浆体与锚索体、注浆体与锚孔周围岩土体之间的摩擦力及注浆体的剪切强度等因素，共同决定了预应力锚索的极限抗拔力，具体计算公式如下[9]。

锚索体与注浆体之间的极限承载力：

[P1=πdsldc1kb]                                  （5）

注浆体与周围岩土体之间的极限抗力：

[][P2=πdvldc2kb]                                （6）

注浆体的极限剪切强度：

[P3=πdsldc3kb]                                    （7）

式中，[kb]为安全系数，常取1.5;[c1]为锚索与灌浆体之间的粘结力;[ld]为锚固端长度;[ds]为锚索体直径;[c2]为注浆体与锚孔内部岩体之间的粘结力;[dv]为钻孔直径;[c3]为注浆体的粘聚力。

2.3 锚索锚固段位置及锚固段长度的确定

锚索的锚固段应完全位于软弱结构面之下;同时，为了锚索的张拉，还应与结构面保持0.2～0.5m的距离。[lsa]、[la]这二者中较大值作为锚索锚固段长度[10]。计算公式为：

[lsa=Fs2Ptπdsτu]                              （8）

[la=Fs2Ptπdhτ]                               （9）

式中，[Fs2]为锚固段抗拉安全系数;[ds]为钢绞线组成锚索体的外表面直径，m;[dh]为注浆体直径，m;[τu]为锚索体与注浆材料之间的粘结强度，MPa;[τ]为锚孔内部岩土体与注浆材料之间的粘结强度，MPa。

2.4 每束锚索钢绞线根数

选用钢绞线强度及单孔预应力锚索锚固力共同确定：

[n=Fs1PtPu]                              （10）

式中，[Fs1]為安全系数，一般取值1.7～2.2;[Pu]为钢绞线极限张拉载荷，kN。

2.5 锚索锚固角度确定

根据规范可知，锚索最优锚固角计算公式为：

[β=45°A+1+2A+12（A+1）φ-α]                   （11）

式中，A为锚固段长度与自由段长度之比;[φ]为滑移面内摩擦角;[α]为滑移面倾角。

2.6 仰坡剩余下滑力的确定

剩余下滑力的确定依据以下相关模型和计算得到，若第i块滑坡体单元上共有[n]束锚索穿过，其中[j（j=1，2，…，n）]每束锚索的锚固力为[Pt]，且穿过m块滑坡体单元，则第i个块滑坡体单元所分担的锚固力[Pi]的计算公式为：

[Pi=j=1nPtm]                           （12）

若传递系数法计算加锚仰坡第i块滑坡体元的稳定性安全系数为[Fsi]，计算公式为：

[Fsi=RiTi]                          （13）

[Ti=KWisinαi+Ei-1cos（αi-1-αi）]      （14）

[Ri=Wicosαi+Ei-1sin（αi-1-αi）+Pisin（αi+θi·tanφiciLi+Picos（αi+θi）]   （15）

[Ei=Ri-Ti]                        （16）

式中，[K]为稳定性计算时采用的安全系数，根据《公路路基设计规范》（JTG D30—2015）的要求，计算剩余下滑力时安全系数要求最小为1.30。

3 工程实例

3.1 工程概况

该隧道最大埋深85m，属于深埋隧道，褒河左岸河谷坡脚处进洞，仰坡坡度为75°，不存在隧道偏压情况，自然状态下仰坡基本稳定。从开挖断面清晰可见表层为坡积土。该仰坡整体岩层岩性及构造为强风化的暗红色砂性岩层与强风化的浅灰色片麻岩互层，岩层倾角为42°，岩层产状为24°，在力学属性上明显存在连续性的层状构造。洞口段围岩等级为IV～V级。以右线洞口段顺层仰坡为分析对象，进行仰坡稳定性评价分析及加固措施研究。

3.2 自然状态下顺层仰坡稳定性计算

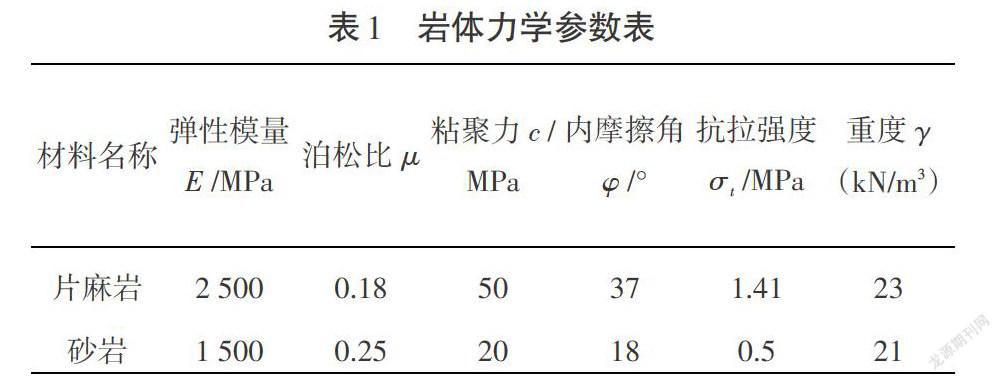
运用传递系数法对自然状态下仰坡稳定性进行理论分析，不考虑隧道开挖对仰坡稳定性的影响。岩体的强度准则采用Mohr-Coulomb准则，通过理正软件中抗滑桩设计模块（传递系数法）分析模块，分析自然状态下顺层仰坡的稳定性。通过查阅仰坡的工程地质勘察资料，确定该仰坡岩体力学参数如表1所示。

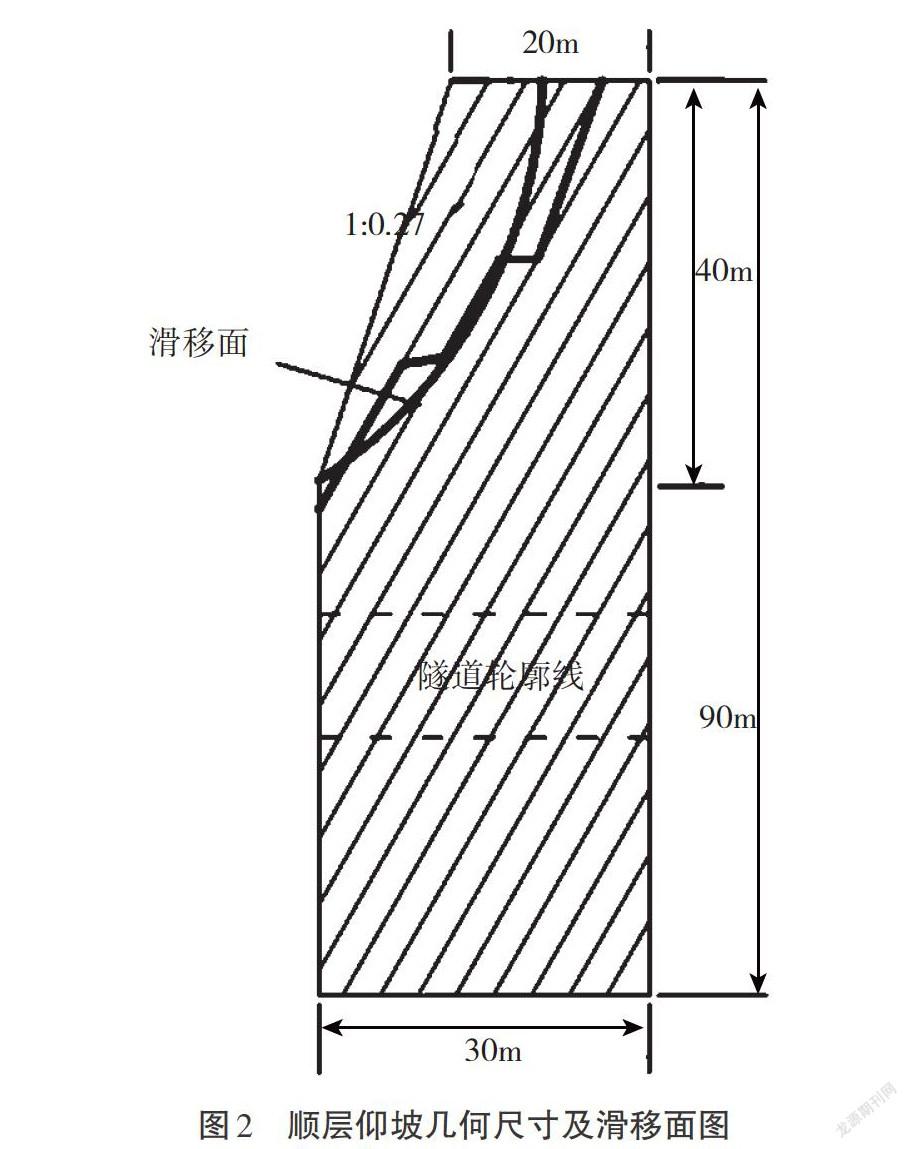
根据仰坡位置，该顺层仰坡采用曲面型滑移面。建立仰坡几何模型时，假设顺层仰坡岩体由两种不同岩性互层组成，岩层倾角42°、岩层厚2m。顺层仰坡几何尺寸及滑移面图见图2。

通过理正软件分析计算得到此仰坡的剩余下滑力为683.4kN，仰坡的稳定性系数为0.98。根据《公路路基设计规范》（JTG D30—2015）的要求，计算剩余下滑力时安全系数不应小于1.3，故在施工之前必须对仰坡采取加固措施，这样才能确保隧道安全。

3.3 加固方案

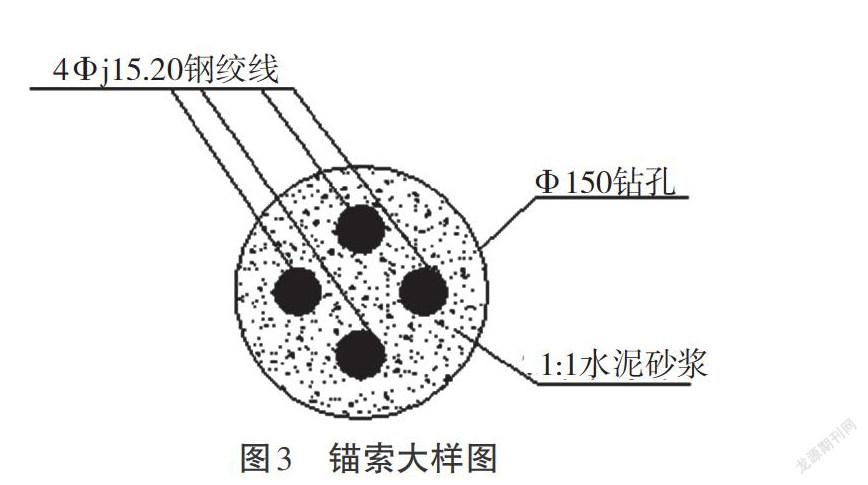
依据工程勘察及设计资料，錨孔直径取Φ150mm，锚索强度为1 860MPa，公称直径为15.20mm，单根低松弛钢绞线的极限张拉力[Pu]=260kN，可知[Fs1]=1.8，根据公式（11）得：[n]=3.6，则预应力锚索主索体由4根钢绞线组成，则4根钢绞线构成的锚索外表直径[ds]=0.034 8m，锚孔直径[dh]=0.15m。锚索大样如图3所示。令[Fs2]=4，注浆材料强度为30MPa。

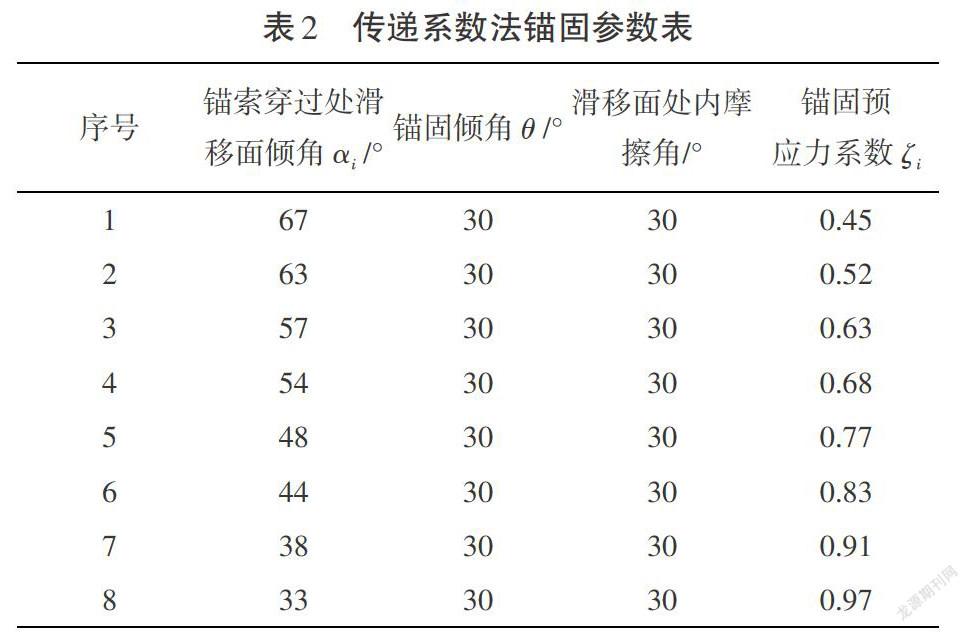
根据公式（1）至公式（5）及公式（11）计算锚固参数，结果如表2所示。

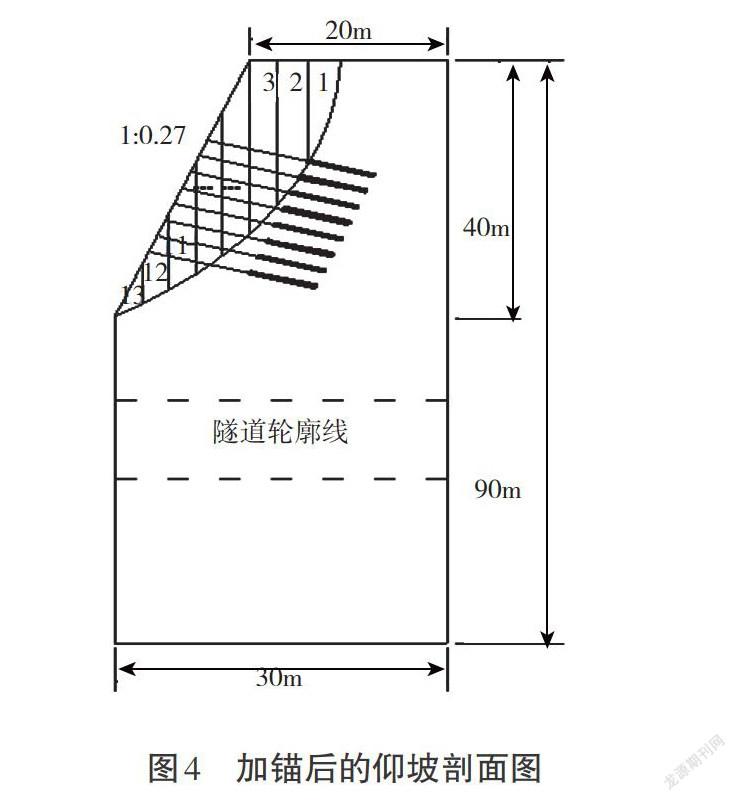
基于传递系数法的自然状态下顺层仰坡的剩余下滑力[E]=683.4kN。根据公式（4）得，每束锚索锚固预应力[Pt]=389kN。根据公式（8）、（9）可得：[lsa]=3.34m，[la]=9.5m，所以改进锚固力算法的锚索锚固段最小长度为9.4m，最终取锚索的锚固端长度为10m，满足预应力锚索锚固段不得大于10m规定。由于滑移面深度最深为15m，锚索锚固段要深入滑移面以下，故锚索自由段取值为15m，锚索总长度为[A=B+C]=10+15=25m。加锚后仰坡剖面图如图4所示。

3.4 加锚后仰坡的稳定性分析

隧道开挖采用二台阶法开挖，运用MIDAS/GTS对隧道洞口顺层仰坡建模分析，下面将对实际建模过程及结果进行介绍。

3.4.1 模型建立及网格划分。根据圣维南原理，模型径向长度为70m（影响范围取3倍洞泾），沿着隧道路线方向取25m，以隧道轴线为中心向上取50m（5倍洞泾），向下取40m（4倍洞泾），模型总体尺寸为[x×y×z]=70m×25m×90m。仰坡网格尺寸为2m，隧道网格尺寸为1m，隧道开挖进尺为2.5m。整体模型网格划分图如图5所示，仰坡锚索布置及网格划分如图6所示。

依据《建筑边坡工程技术规范》（GB 50330—2013），锚索选用永久性拉力型锚索。在数值模拟中，锚索自由段采用植入式桁架单元，植入式桁架无须考虑单元体与土体间节点的耦合;锚固段采用植入式梁单元，无须考虑节点的耦合。数值模拟材料的物理力学参数如表3所示。

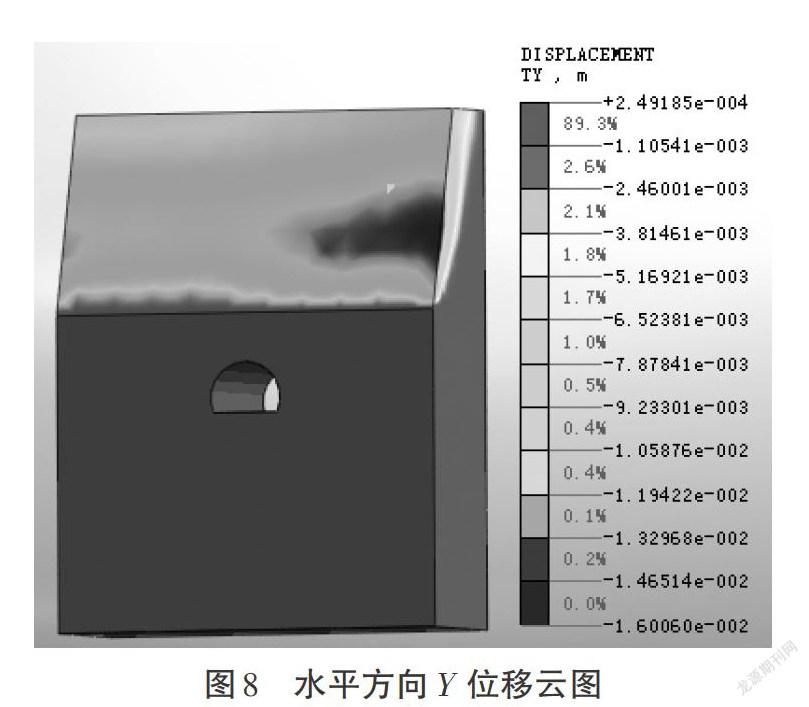
3.4.2 加固后计算结果及仰坡稳定性评价。本隧道模拟开挖10个进尺，分析加锚后仰坡稳定性。加锚后开挖隧道的顺层仰坡水平位移云图（限于篇幅，只提取开挖第10个进尺后的云图）见图7和图8。

通过分析加固后仰坡水平位移云图可得出以下结论。

①第10个进尺开挖完成后，坡顶关键点的水平位移在[X]方向最大为0.29mm，在[Y]方向最大为5.96mm，分别出现在仰坡顶部的左端和右端。对于此类围岩，查阅《公路隧道设计规范》（JTG D70—2004），按照每24h 1个进尺的速度开挖，10个进尺需要10d完成，通过计算，水平[X]方向平均位移速度为0.025mm/d，水平[Y]方向平均位移速度为0.60mm/d。根据《建筑边坡工程技术规范》（GB 50330—2013），边坡支护结构坡顶的最大水平位移不应超过2mm/d，否则应采取应急措施，而石门隧道洞口仰坡经锚索加固后坡顶平均水平位移在两个方向均未超过此标准，说明了加锚后仰坡稳定。

②利用MIDAS有限元分析软件中边坡稳定性分析模块，得出此仰坡的稳定安全系数为1.412，大于《公路路基设计规范》（JTG D30—2015）中稳定安全系数不应小于1.3的要求，表明仰坡已处于稳定状态。

4 结论

通过对锚索加固设计理论的研究，提出了锚索加固设计方法，并运用在宝汉高速石门隧道洞口仰坡加固中，得出以下结论。

①利用传递系数法进行分析计算，计算结果表明，自然仰坡若不加固会使仰坡在隧道开挖时发生滑移，丧失稳定性。因此，必须对仰坡进行加固。

②结合宝汉高速石门隧道具体工程实例，运用有限元分析软件MIDAS/GTS对隧道开挖施工阶段的仰坡稳定性进行模拟，计算结果表明，加锚后的仰坡安全稳定系数大于规范规定限值，表明加锚后仰坡具有稳定性。

参考文献：

[1]王帅帅，高波，隋传毅，等.不同地质条件下隧道洞口仰坡地震破坏特性研究[J].岩土力学，2014（S1）：278-284.

[2]卢海峰，陈从新，袁从华，等.巴东组红层软岩缓倾顺层仰坡破坏机制分析[J].岩石力学与工程學报，2010（S2）：3569-3577.

[3]赵晓彦.花岗岩类土质仰坡主被动组合锚固设计方法[J].岩石力学与工程学报，2013（23）：165-169.

[4]王涛，吴树仁，石菊松，等.国内外典型工程滑坡灾害比较[J].地质通报，2013（12）：1881-1899.

[5]林杭，曹平.锚杆长度对仰坡稳定性影响的数值分析[J].岩土工程学报，2009（3）：470-474.

[6]潘瑞林，李秉生，蒋爵光.板裂结构岩体顺层仰坡溃屈破坏的研究[J].西南交通大学学报，1990（3）：82-88.

[7]鲜杰良.砂泥岩互层顺层岩质滑坡成因机制及开挖响应研究[D].成都：成都理工大学，2014.

[8]冯春，李世海，王杰.基于CDEM的顺层仰坡地震稳定性分析方法研究[J].岩土工程学报，2012（4）：717-724.

[9]唐浩.顺层岩质边坡稳定性影响因素分析[D].武汉：武汉理工大学，2009.

[10]刘桂宏.地下工程预应力锚索支护设计参数研究[D].重庆：重庆交通大学，2014.