基于灰色理论的陇南市旅游人数预测

摘要：随着人民生活水平的提高和生活方式的转变，使得人们越来越注重旅游，观光旅游和休闲度假旅游已成为当前的主要度假方式。旅游过程不但有利于人身心健康发展，也能使得精神境界得到提升。与此同时，旅游也可以助力精准扶贫，实现对当地经济的带动作用。以预测陇南市未来旅游人数为研究目的，基于灰色系统理论预测旅游带来的顾客人数，以2009年至2016年陇南市旅游人口为初始数据，通过建立GM（1，1）模型对未来八年陇南市旅游人数进行了预测，从而反向指导旅游开发，预测结果显示在未来几年陇南市旅游人数呈逐年增加，而且有仍将继续上升的趋势。

关键词：灰色理论;旅游;预测;GM（1，1）

中图分类号： F592                      文献标识码：A

陇南市位于甘肃南部，东邻陕西，南接四川，位于秦巴山区、青藏高原、黄土高原三大地形交汇区域。境内地貌俊秀，气候宜人，森林覆盖率高，素有“陇上江南”之美称。丰富的旅游资源使得陇南发展旅游业有着得天独厚的优势，而独特旅游资源地区往往与贫困乡村地区存在着很大的重合性，这就使发展旅游业与扶贫之间建立了有机联系。旅游扶贫是典型的产业扶贫形式，借助于旅游经济对区域经济的带动作用而脱贫。

灰色系统是邓聚龙教授提出的一种新的系统理论[1]，利用灰色系统理论的主要优点是通过一系列数据生成方法将本没有规律的、杂乱无章的或规律性不强的原始数据序列变得具有明显的规律性，解决了数学界一直认为不能解决的微积分方程建模问题。显然，灰色系统理论应用到预测中只需具有连续性的时间序列，不需要太多数据且预测精度高，不仅具有高度的概括性，而且使预测精度高，具有明显的确定性[2]。由于需要的样本数据少， 建模建立简单， 预测精度高， 计算方便， 不需要考虑分布规律等优点而被广泛应用[3]。旅游人口预测问题为一个复杂的非线性系统，样本数据量少，变化规律不确定的系统。如果使用神经网络算法很难取得理想的效果，故考虑采用GM预测来预测未来的旅游人数。

1. GM（1，1）模型的基本原理与分析过程

灰色系统理论首先基于对客观系统的新的认识.尽管某些系统的信息不够充分，但作为系统必然是有特定功能和有序的，只是其内在规律并未充分外露.有些随机量、无规则的干扰成分以及杂乱无章的数据列，从灰色系统的观点来看，并不认为是不可捉摸的.相反地，灰色系统理论将随机量看作是在一定范围内变化的灰色量，按适当的办法将原始数据进行处理，将灰色数变换为生成数，从生成数进而得到规律性较强的生成函数[3]。

灰色系统常用的预测模型是GM（1，1）模型，GM（1，1）模型表示一阶的、单变量的线性动态预测模型，其预测原理是将离散的随机数，经过生成变成随机性被显著削弱的较有規律的生成数，在此基础上建立数学模型，建模步骤如下[4]：

2.基于GM（1，1）模型的陇南市旅游人数的预测分析

陇南市地理环境复杂，旅游资源丰富，旅游也是当地经济的主要来源，而且随着陇南市旅游投入和开发的不断加大，随着当地对旅游的重视力度加大和人民生活水平的提高，旅游人数最近几年已成持续上升的趋势。以下（表2）是2009年至2016年陇南市旅游数。

（1）生成新序列

根据表2之数据得到陇南市旅游人数的原始序列为

经过一次累加得到新序列

（2）构造矩阵B和Yn

（3）求参数向量

（4）求预测模型

由预测模型可算得预测值及误差（表3）

（5）精度检验

由表3可得残差均值及原始数据平均值，它们分别为 =-2.2， =632.05，由此又可得 =701.628， =120506.978。因此，后验差比值为C=0.25246<0.35，故预测精度等级为好。

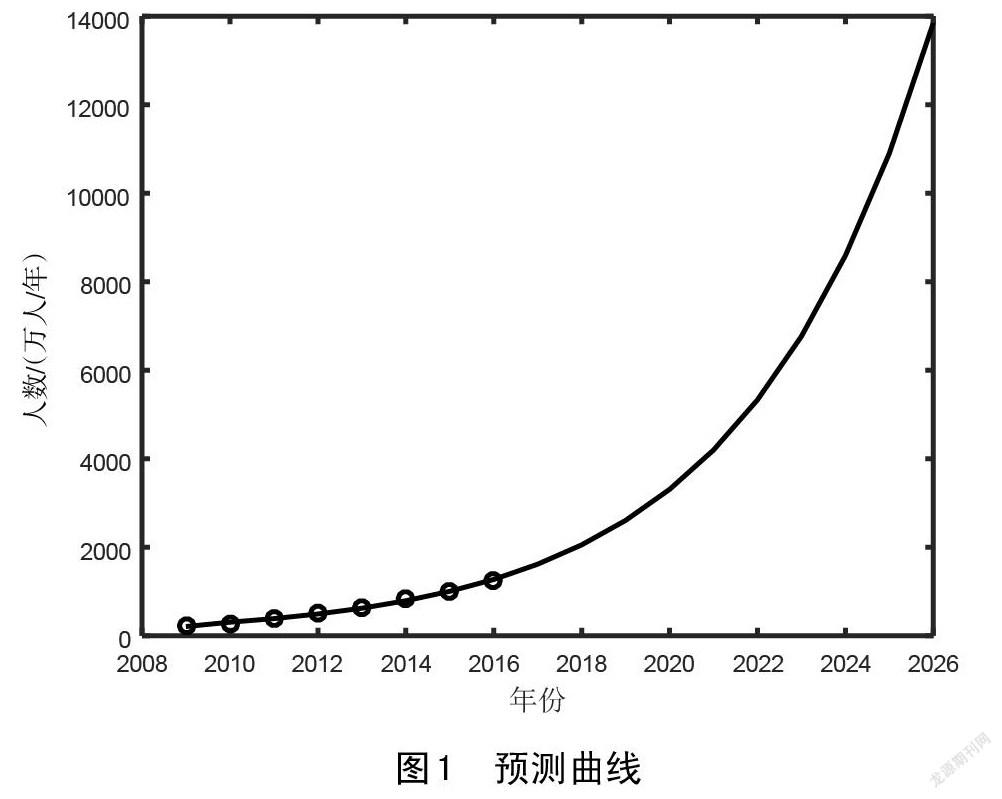
通过预测数据做出上图，在图中也发现预测数据和实践的2009-2016年数据基本接近，曲线拟合度比较高，所以该方法用来预测陇南市旅游人数方法科学可行。

（6）未来八年的预测

预测结果显示，未来几年陇南市旅游人数将持续上升。

3结语

本文基于灰色系统理论构建的GM（1，1）模型通过原始时间数据，从而根据这种规律预测未来几年陇南市旅游人数。通过后验差比值检验，证明该灰色系统预测精度高，能够客观反映目前陇南市旅游人数呈逐年上升的总趋势。利用灰色系统对陇南市旅游人数进行高精度预测，反映出当前及未来陇南市对旅游业发展必须引起重视，集中精力搞好旅游，通过旅游带动当地扶贫。

参考文献

[1]邓聚龙.灰色系统基本方法[M].武汉：华中理工大学出版社， 1987.

[2]杨超. 基于灰色理论和神经网络的中长期电力负荷预测的研究[B]. 天津理工大学，2015：1-26.

[3]孟祥星.田成微.冬雷等. 灰色理论用于风力发电容量中长期预测的研究[J]. 电力系统保护与控制，2011，39（21）：81-84.

[4]孟东平，从生成数进而得到规律性较强的生成函数[B]. 西南交通大学，2009：43-75

[5]冀荣华，李鑫，郭敏英等. 基于GM（1，1）模型群的农田土壤墒情短期预测[J]. 农业机械学报，2016， 47（10）：401-407.

作者简介：程军锋（1980—）男， 甘肃礼县人， 讲师， 研究方向：数据库与数据挖掘.系统建模与仿真。

联系方式：手机：13993978821       信箱：chengjunfeng@163.com