渗流一应力耦合作用下的临库竖井开挖数值分析

2019-09-10曾祥茜何文社王开喜

人民黄河 2019年4期

曾祥茜　何文社　王开喜

摘要：竖井式地下泵站是引水工程中获取优质水源的必要手段，临库竖井特殊的地质环境，成为制约其安全施工的重要因素。针对临夏州引黄济临工程竖井式一级取水泵站，利用FLAC3D有限差分软件模拟竖井的开挖过程，对比分析了渗流一应力耦合及非耦合作用下竖井应力变形规律。结果表明，在临界浸润面处，井壁变形值最大，且井口位移与井底中心回弹量均随着竖井开挖深度增大而增大。渗流一应力耦合作用时，竖井井壁围岩受力变形均处于较为不利的状态，在竖井开挖完成时井底出现应力值突变。因此在实际施工过程中，考虑渗流一应力耦合作用下的竖井变形更为准确。

关键词：引水工程;临库竖井开挖;渗流一应力耦合;FLAC3D：数值分析

中图分类号：TV675;TU433

文献标志码：A

doi：10. 3969/j .issn.1000- 1379.2019.04.031

竖井式地下泵站是引水工程中获取深层优质水源的必要手段。临近水库由于其特殊的地质环境，地下水资源丰富，渗流场十分复杂，地质条件对竖井开挖极为不利。由于竖井开挖过程中动力因素的扰动，井壁土体的属性随着竖井开挖过程中的卸荷作用而逐渐变差，土体的孔隙结构发生变化，从而导致围岩渗透系数及渗透力的改变，而渗流场的改变将直接影响围岩结构属性及物理力学性能，进而改变围岩结构体的应力平衡状态[1-2]，加之复杂的地质条件，极有可能造成管涌、坍塌等后果[3]。本文以临夏州引黄济临工程为例，取其一级取水泵站竖井为研究对象，利用FLAC3D有限差分软件进行施工过程的三维数值模拟[4-6].基于耦合与非耦合两种计算模式，对比分析竖井施工过程中位移场及应力场的变化规律[7-8].研究渗流一应力耦合作用对竖井围岩受力变形的影响，以此为工程实际施工提供相应借鉴。

1 工程概况

1.1 泵站结构

临夏州引黄济临工程一级取水泵站位于刘家峡水库库区，为临库正向取水。厂区主要由引水暗涵、进水闸室、进水前池、主泵室、副厂房、安装间、临库侧护岸等组成。泵站主厂房为圆形竖井结构，内径25.00 m，壁墙厚度2. 00 m，深28. 30 m。厂区开挖地坪高程1 738.65 m.主泵室井底开挖高程1 710.35 m。

1.2 地质构造及水文条件

该取水枢纽位于刘家峡水库南岸莲花码头东南处，施工期间，水库水位为1 715.35 m，基坑较深，地下水资源丰富，渗流场较为复杂，施工期间要确保边坡稳定，合理疏导排水，确保井口土体稳定是保证基坑施工安全的重点[9]。根据设计地质勘测资料及现场勘察，泵站主泵室高程1 738.65 m至1 724.00 m为坚质黏土夹杂砾石，属第四系全新统滑坡堆积04。标高1 724.00 m以下为新近系上统临夏组砂岩、砂质泥岩。厂区上部坚质黏土含砾较少，下部含砾并夹有少量泥岩孤石，土体稍密，上部土体较干、下部稍湿。下部基岩为新近系泥岩夹砂岩，岩体透水率为3.69-4.92 Lu，上下部土体透水性均较好。

2 数值模拟

2.1 计算模型及边界条件

为充分反映竖井开挖横断面相邻围岩的变化情况，模型尺寸水平方向（X、Y方向）分别取井口约7倍洞径，为210 m.竖井开挖方向（Z方向）取210 m[10]。开挖竖井为直径29 m，高28 m的圆柱体。

竖井开挖过程会对初始应力场和孔压场造成多次扰动，应力场将多次重分布。本构模型选用岩土力学通用的Mohr- Coulomb模型，围岩采用实体单元和理想弹性材料模拟;渗流模式下选用各向同性渗流模型，不考虑土颗粒及流体的可压缩性。模型的前后、左右边界为水平约束，下边界为竖直约束，上边界为自由边界。模型的右侧为透水边界，根据地勘报告，在开挖15 m处设置临界浸润面，水头自z=-15 m处至模型底部呈线性分布。模型网格划分剖面如图1所示。

数值模拟过程服从以下设定[11]：①竖井开挖按5m为一个循环进尺，分为6个工步进行掘进;②初始应力场由自重场构成，且忽略构造应力：③由于计算模型为正六面体，且竖井开挖断面呈对称分布，因此取模型一半进行分析。

2.2 物理参数

根据地质勘测资料及现场勘察，竖井标高1 738.65 m至1 724.00 m（即模型z=-15 m以上）段为坚质黏土夹杂砾石，土体较干，属第四系全新统滑坡堆积02el为Ⅳ类围岩。标高1 724.00 m以下（即模型z=-15 m以下）為新近系上统临夏组砂岩、砂质泥岩，土体稍湿，渗透系数为4. 48×10 cm/s，为V类围岩。其围岩计算力学参数见表1。

3 数值模拟结果分析

FLAC3D在分析含有孔隙水压力的相关问题时，可根据是否设置流体计算，分为两种计算模式[12]：非耦合计算模式通过纯力学因素扰动来计算竖井开挖过程中位移和应力的变化规律.渗流一应力耦合计算模式将考虑流体和力学相互扰动的耦合作用。通过分析对比两种计算模式下竖井施工过程中的受力变形情况，得出渗流场对位移场、应力场的影响规律。

3.1 初始应力场和孔压场

未开挖之前地层初始状态下的应力场和孔压场云图如图2、图3所示，可以看出，土体的应力分层均匀，从上至下应力值逐渐增大，最小地表应力为0.039 MPa，模型底部的最大应力为4.510 MPa。透水边界的孔隙水压力呈梯度分布，模型上部孔压为零，右边界底部孔隙水压力最大为1.950 MPa.逐渐向土层渗流并有明显的渗流路径，以至达到稳态平衡。由此可知，随着开挖的进行，竖井底部围岩受力增大，且在含有地下水的施工阶段，初始孔压场将随着竖井开挖进行二次分布，地下水也随着产生的水头差而大量渗入临空面。因此，在实际施工过程中应及时做好初期支护及防渗、排水工作，预防围岩受力较大且受渗流作用影响而属性变差。

3.2渗流一应力耦合及非耦合计算模式下的位移变化规律

3.2.1 井壁水平位移分析

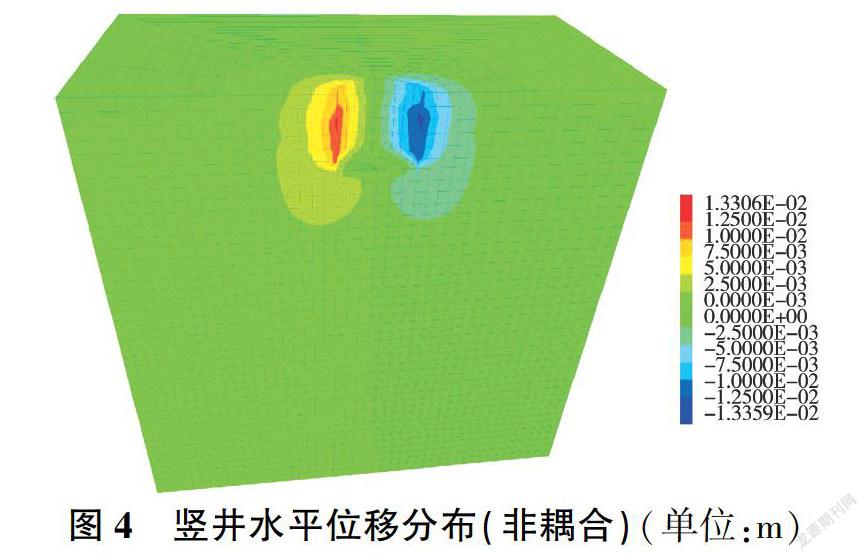
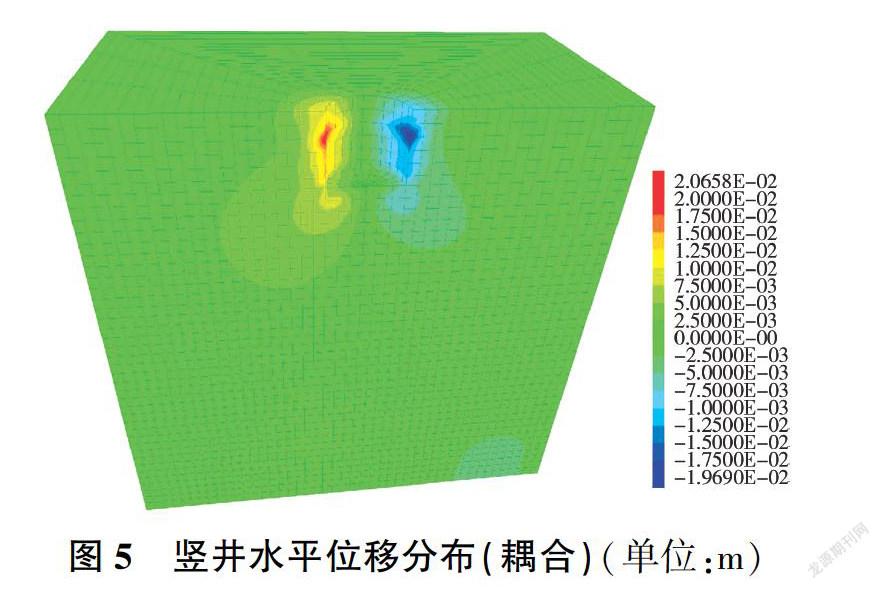
图4、图5为两种计算模式下竖井开挖完成时的水平位移分布云图。非耦合计算模式下，竖井在开挖至10 m及以下时，井壁的水平向位移都较大，最大为13.30 mm;渗流一应力耦合计算模式下，其最大水平向位移为20.60 mm，发生在深度10 m处，10 m以下井壁水平向位移逐渐减小但仍大于非耦合时。这是由于水库的浸润线在开挖15 m处，非耦合计算模式下进行第四步（即15 m以下）竖井开挖时考虑井底积水而进行抽水，在抽水之后土体发生固结，因此位移有减小的趋势。相较于非耦合，耦合时的土体因其卸荷作用与含水后结构属性变差，井壁土体较为松弛，故水平向位移较大。

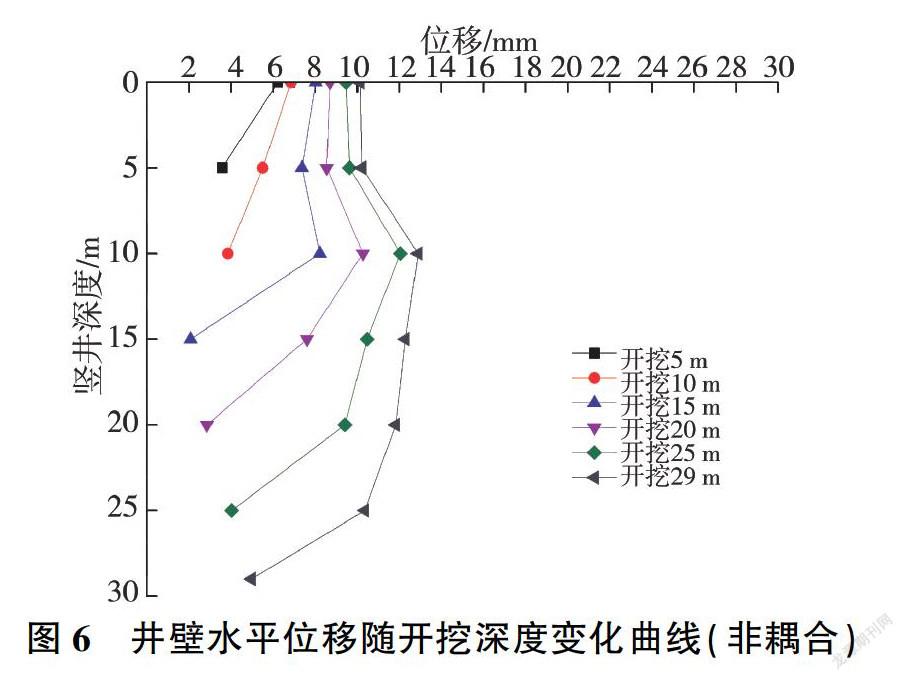
图6为非耦合计算模式下位移变化曲线，可以看出：开挖前Sm时，井壁位移随开挖深度的增加而减小：在开挖5-10 m时，井壁位移随开挖深度的增大而增大，在开挖10 m处位移最大：开挖10 m以下时，井壁位移随开挖深度的增大而减小。

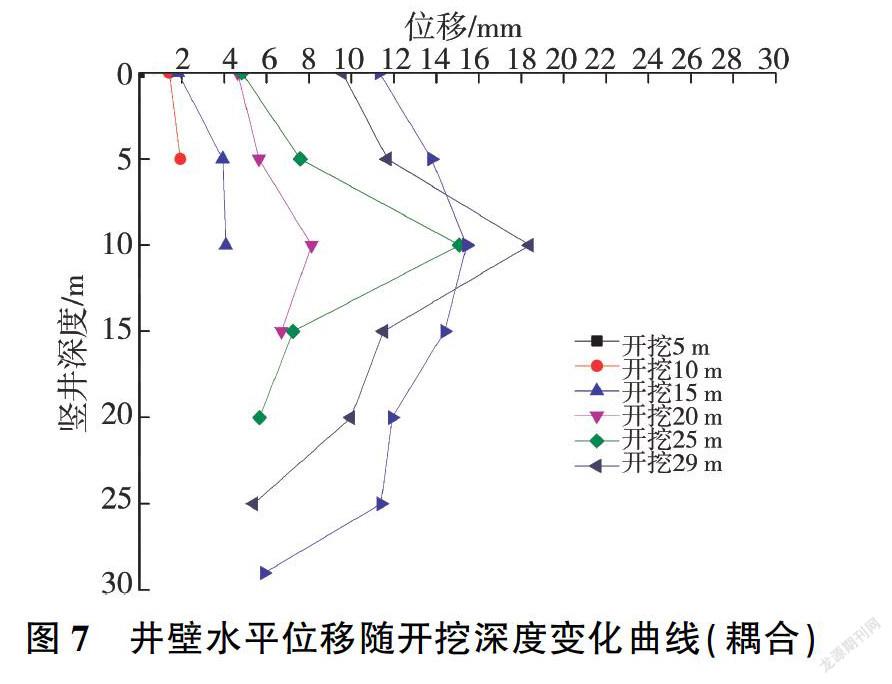
图7为渗流一应力耦合计算模式下位移变化曲线，可以看出，井口（竖井深度为零）、井壁的位移，均随开挖深度的增大而增大。在开挖0-10 m时，井口的位移范围仅为1-2 mm.井壁的位移范围仅有2-4 mm，位移范围较小;在开挖15-20 m时，井口位移范围为4-5 mm，由开挖20 m的变化曲线可以看出，在竖井深度为10 m处，井壁有最大位移15.13 mm;开挖25-29 m时，井口最大位移为11.35 mm，由开挖25 m的变化曲线可以看出，在竖井深度为10 m处，井壁有最大位移18.40 mm。

从图6、图7的变化曲线得出，每一施工步的开挖都将造成位移场的重分布以至达到再次平衡。尤其在渗流一应力耦合计算模式下，随着竖井的不断开挖，井壁的围岩属性逐渐变差，进而造成井壁的动态变形，在井口处位移突变，在z=-10 m处，有可能造成井壁土体坍塌。在施工过程中，应加强井口及每一次开挖后井壁的支护，以及在z=-10 m处对土体采取永久支护和加固措施。

3.2.2 井底竖向位移分析

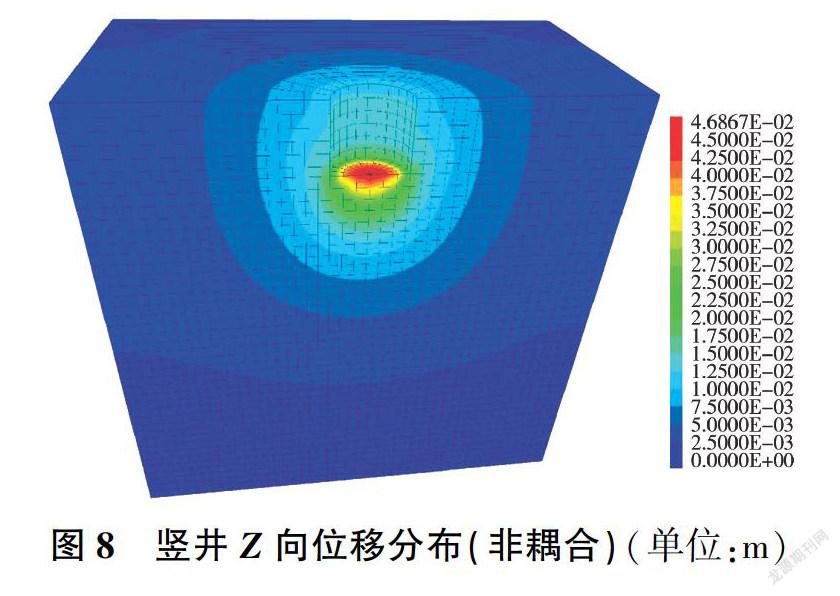
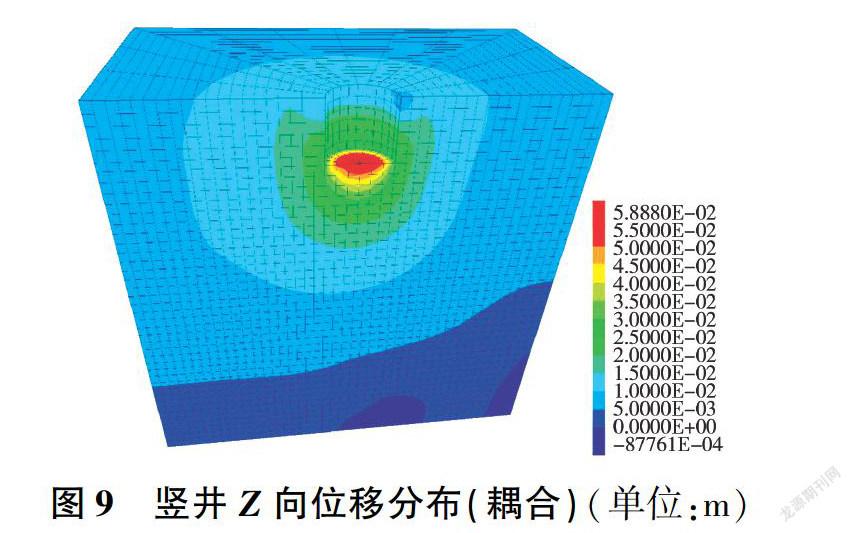
图8、图9为竖井在完成开挖后的Z向位移分布云图，可以看出，渗流一应力耦合计算模式下的竖向位移影响区域较非耦合时大。非耦合计算模式下，竖井开挖回弹量最大值在井底中心，最大回弹量为4.68cm;渗流一应力耦合计算模式下，最大回弹量为5.88 cm。在施工过程中，由于土体的卸荷作用，井底土体回弹而变得松弛，其蠕变也会导致井底的隆起，在考虑渗流影响的情况下，土体会吸水膨胀，以及施工时间的长短、一次性开挖的深度等都会引起井底回弹量的变化，因此在施工过程中应该考虑上述因素，避免井底回弹量过大导致不必要的工程灾害。

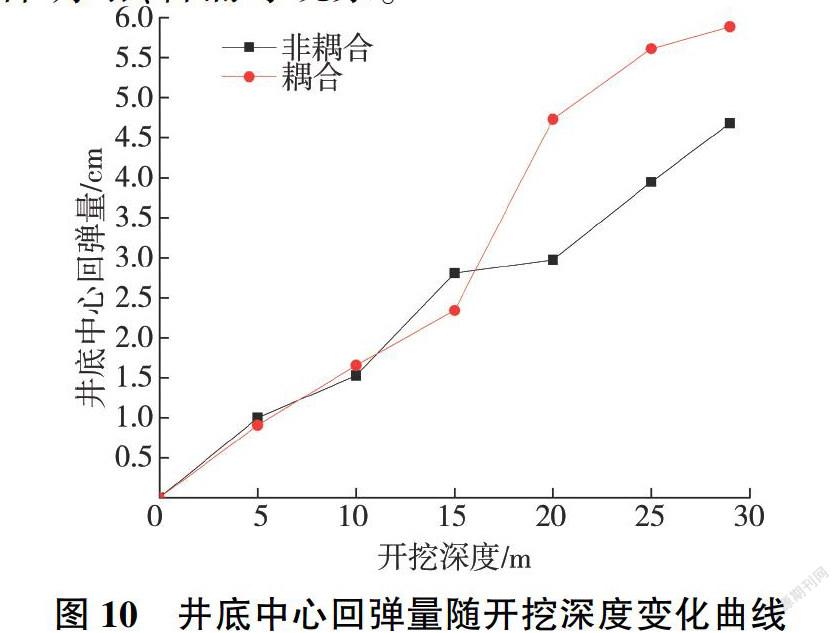
图10为在非耦合和耦合两种计算模式下井底中心回弹量随开挖深度变化的曲线图，可以看出，随着开挖深度的增加，井底的中心回弹量也不断增大。两种计算模式下，开挖深度在15 m以上时，因为土体被开挖的土方量相同，所以井底回弹量相差不大：开挖深度在15 m以下时，由于水库渗流的作用，在渗流一应力耦合计算模式下井底的回弹量计算将考虑土方的自重与水压力的双重作用，因此其井底中心的回弹量较非耦合时大。实际施工中，应及时处理井底积水，采取必要的排水措施，着重加强对井壁的永久支护，以避免造成土体坍塌、管涌等现象。

3.3 渗流一应力耦合及非耦合计算模式下的应力变化规律

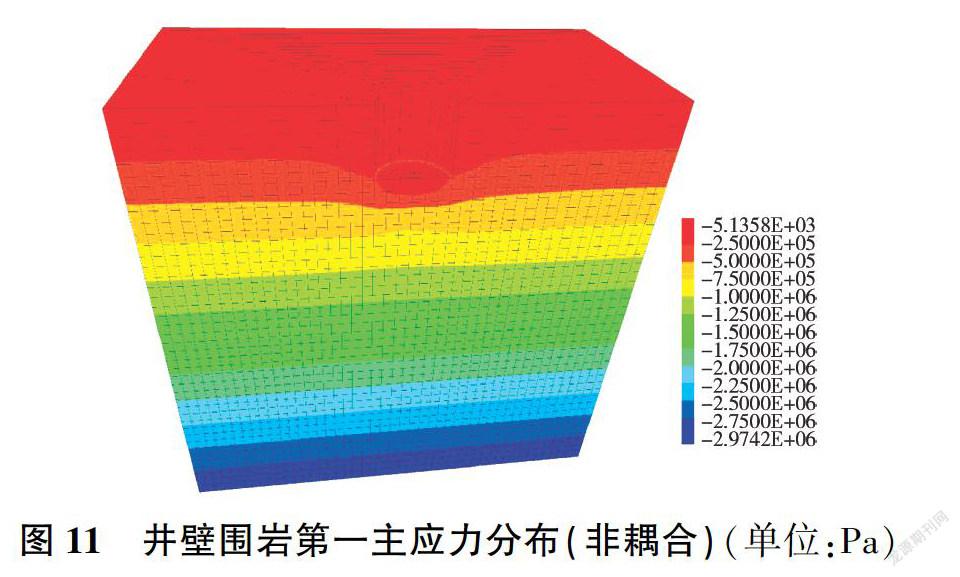
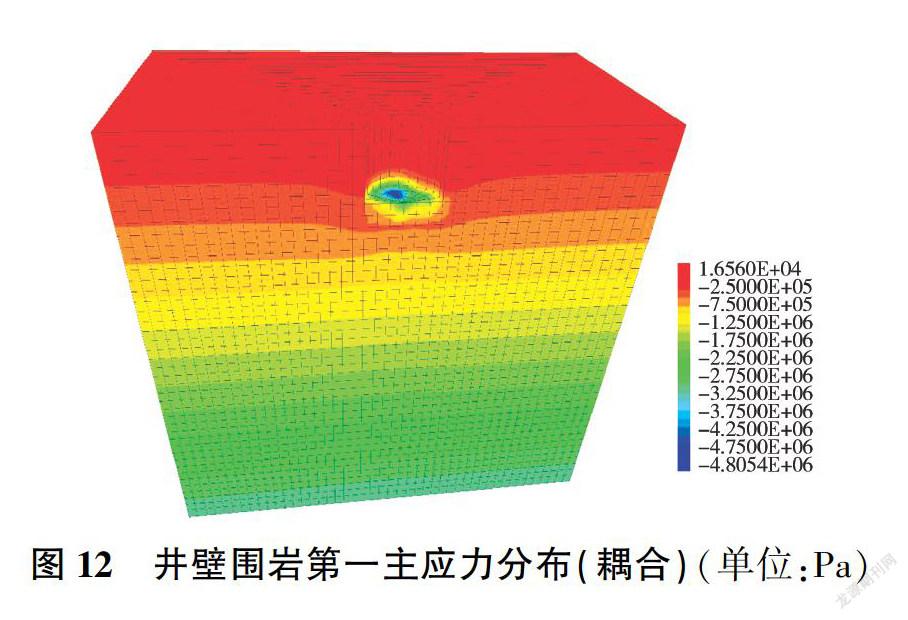
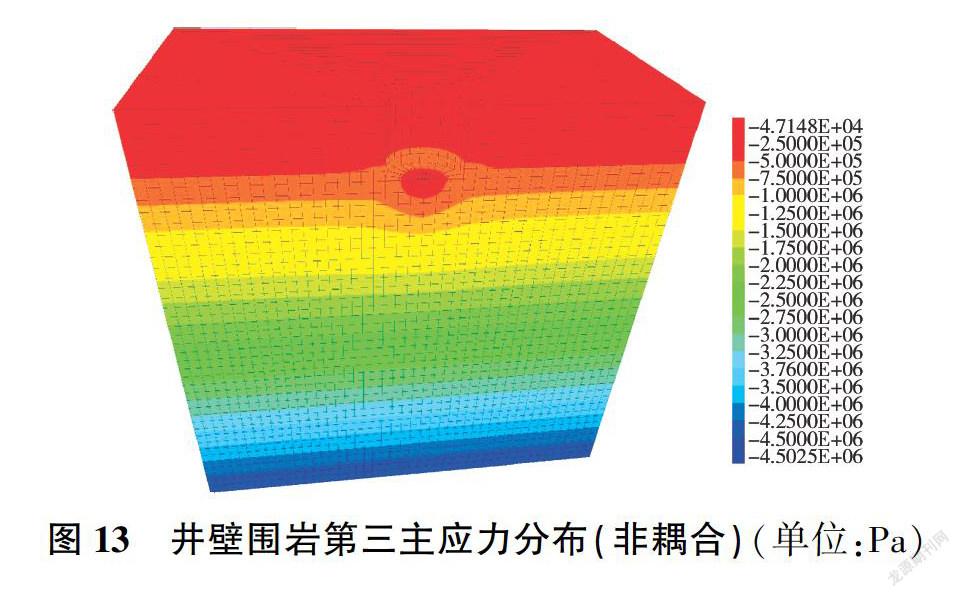
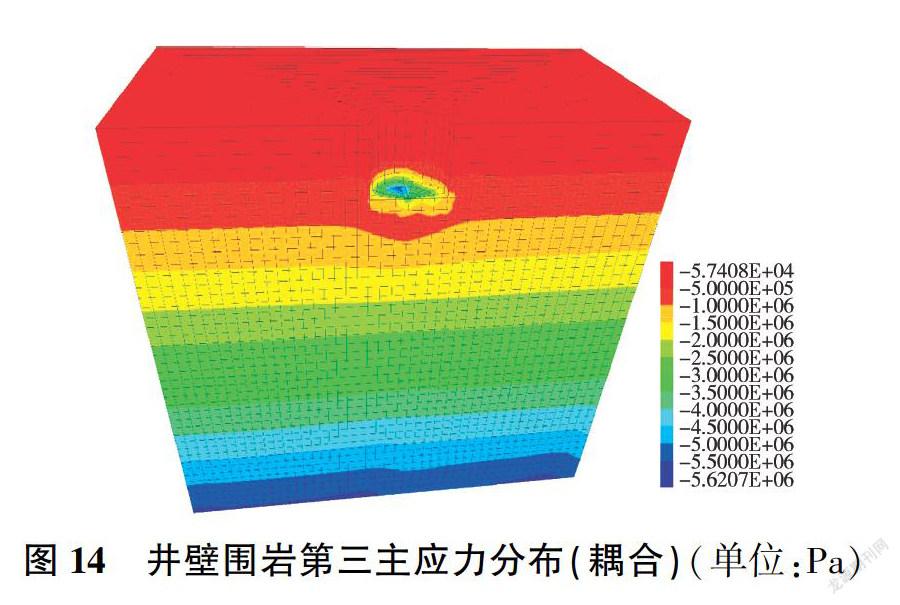
图II-图14为两种计算模式下竖井开挖完成时的第一、第三主应力分布云图，表2为不同开挖深度下井壁第一、第三主应力最大值，可以看出，在两种计算模式下，第一、第三主应力均随开挖深度的增大而增大，开挖深度小于15 m的施工段不含地下水，因此其应力大小基本相近：开挖深度大于15 m的施工段含有地下水，考虑渗流场的影响，渗流一应力耦合模式下第一、第三主应力整体较非耦合时大。非耦合计算模式下应力变化平稳，在完成竖井开挖后其第一主应力为-0.277 MPa，第三主应力为-0.664 MPa;渗流一应力耦合计算模式下，在开挖完成后井底出现应力突变，其第一主应力为-4.800 MPa，第三主应力为-5.170 MPa。由此可见，应在开挖完成时及时做好初期支护，以减小井底回弹量。

4 结论

通过对临库竖井开挖过程的受力变形数值分析，可得到以下结论：

（1）开挖过程的动力因素会造成土体应力场和渗流场的重分布，然后逐渐达到稳定的渗流一应力平衡状态，分析得到了竖井开挖后的井壁变形形态及变形值域。

（2）受渗透力与土压力共同作用，井壁向临空面的变形随竖井开挖深度的增大而增大。在施工过程中，应及时对竖井的井壁和井口处做好衬砌支护措施，以保证竖井结构的稳定性。

（3）对比分析两种不同计算模式下竖井井口受力变形规律可知，渗流一应力耦合作用下竖井开挖的受力变形量较大，故在施工过程中不可忽视水库渗流作用的影响，应及时排水并加强水土分界面的井壁支护，以避免土体塌陷失稳。

（4）渗流一应力耦合作用下，围岩的位移和应力变化均处于较为不利的状态，为避免井底中心的回弹量过大，在施工期间可通过控制竖井的一次性开挖量、开挖时间、井底排水等措施保证工程的安全。

参考文献：

[1] 曾静，盛谦，廖红建，等，佛子岭抽水蓄能水电站地下厂房施工开挖过程的FLAC数值模拟[J].岩土力学，2006 （4）：637-642.

[2]颜勇，地铁深基坑渗流应力耦合研究[J].铁道工程学报，2011，28（6）：92-97.

[3]裴桂红，吴军，刘建军，等，深基坑开挖过程中渗流一应力耦合数值模拟[J].岩石力学与工程学报，2004，23（增刊2）：4975-4978.

[4]代鑫，徐伟，邹丽，等，竖井开挖过程的数值模拟分析[J].岩土工程学报，2012，34（增刊1）：154-157.

[5] 陈育民，徐顶平.FLAC/FLAC3D基础与工程实例[M].北京：中国水利水电出版社，2008：182-209.