平底蛋形断面隧洞正常水深直接计算方法
2019-09-10牛坤华强
牛坤 华强

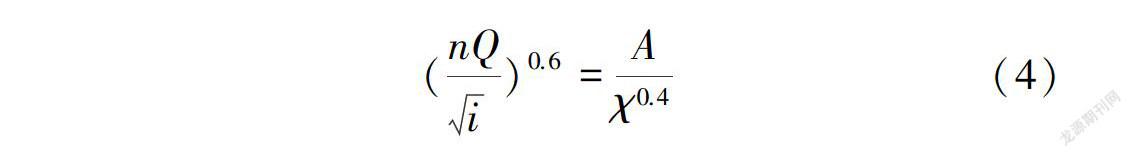

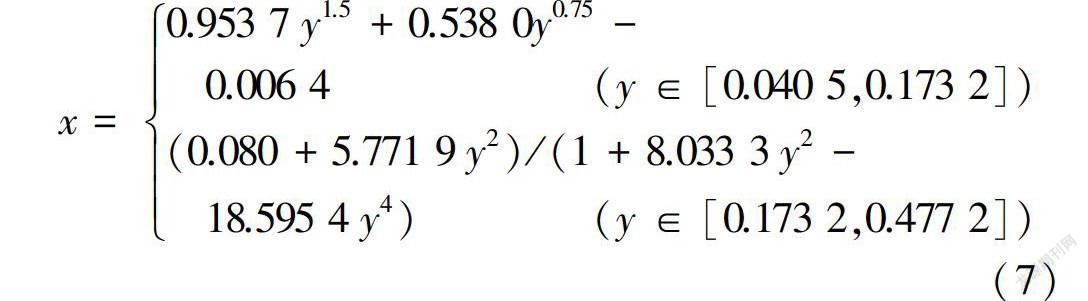
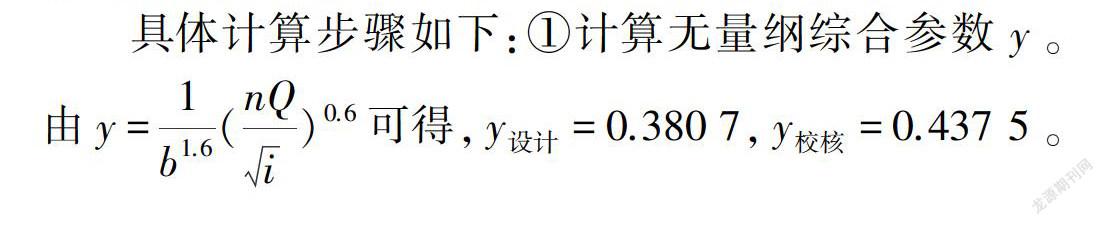

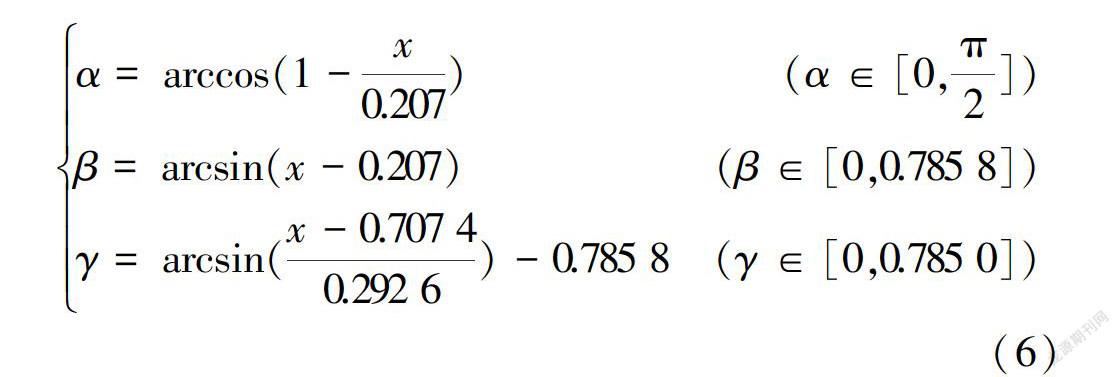

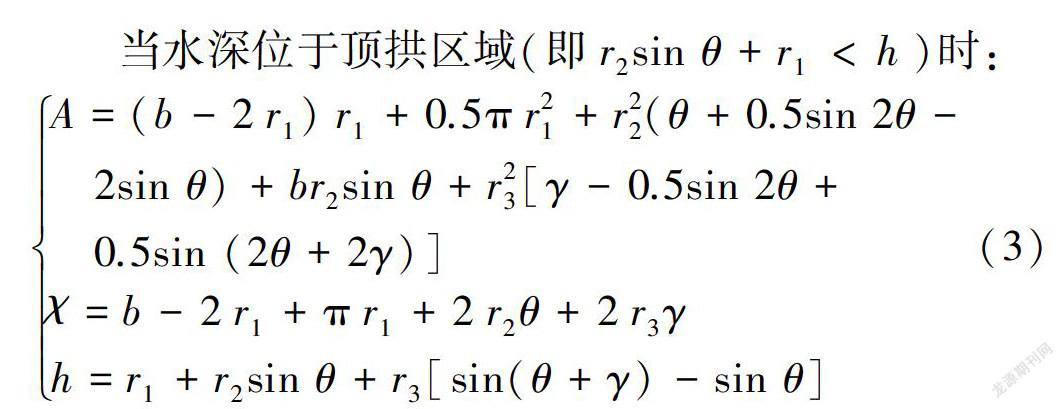
摘要:平底蛋形断面具有施工相对简单、适应性强的特点,但断面形状较复杂,正常水深计算需要求解超越方程,计算过程繁琐且无法直接求解。利用面积分割法计算出普通平底蛋形断面的水力要素方程,得到3种典型断面的过水断面面积、湿周和水深方程。根据正常水深基本方程和优化拟合理论,推导出求解3种平底蛋形典型断面正常水深超越方程的直接简化计算公式,并进行公式精度分析。结果表明,直接简化计算公式具有形式简单、计算方便、精度高的特点,在适用范围内正常水深相对误差最大值仅为0.34%。
关键词:平底蛋形断面;水力要素;正常水深;直接计算
中图分类号:TV133
文献标志码:A
doi:10.3969/j.issn. 1000 - 1379.2019. 04.021
正常水深是明渠水流计算中的重要参数,其传统计算方法主要有试算法、迭代法和查图法等[1],计算过程繁琐且一般无法直接求解。对于常见无压隧洞如城门洞形、马蹄形等断面形式的正常水深计算研究,通过采用拟合优化或迭代算法,已取得了较为实用的成果[2-5]。无压蛋形断面隧洞是排灌工程采用的断面形式之一,结构受力条件良好,水力性能优越,适用于地质条件差、山岩压力大的地质环境。对于普通的六圆弧和四圆弧蛋形断面,文献[6-9]推导出水力要素表达式,并给出了正常水深的直接计算公式。
平底蛋形斷面作为《水工设计手册》[10]推荐的无压水工隧洞专用断面之一,将普通六圆弧蛋形断面的反拱圆弧底调整为平底板,降低了施工难度,具有较好的应用前景。目前,对于平底蛋形断面的水深计算未见研究成果,本文推导了平底蛋形普通断面的水力要素表达式,分析了3种平底蛋形典型断面正常水深隐函数方程,运用拟合优化方法获得该断面形式的简化直接计算公式,为工程应用提供简单、实用的计算方法。
1 平底蛋形普通断面形状特征参数
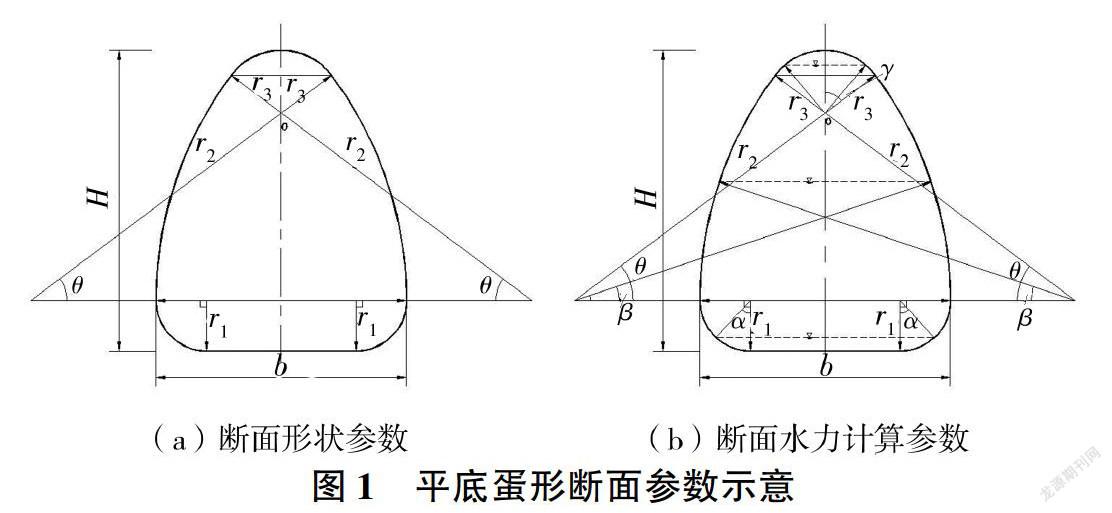
平底蛋形普通断面由5段圆弧和底部水平直线段组成,其断面形状如图l(a)所示。断面最大宽度为b,底部水平直线段两端为1/4圆弧段,圆弧半径为r1;中部扇形区域由半径为r2的两段圆弧围成,圆心位于断面最大宽度处的水平线上,圆心角为θ;顶拱段圆弧半径为r3,圆心位于断面中心线上,对应的圆心角为π一2θ。
2 平底蛋形断面水力要素计算
2.1 平底蛋形普通断面水力要素
根据平底蛋形普通断面的形状特征,不同水深处的过水断面面积A由两侧扇形区、中部矩(梯)形区组合而成,断面水力计算参数如图l(b)所示,则过水断面面积
2.2 平底蛋形典型断面水力要素
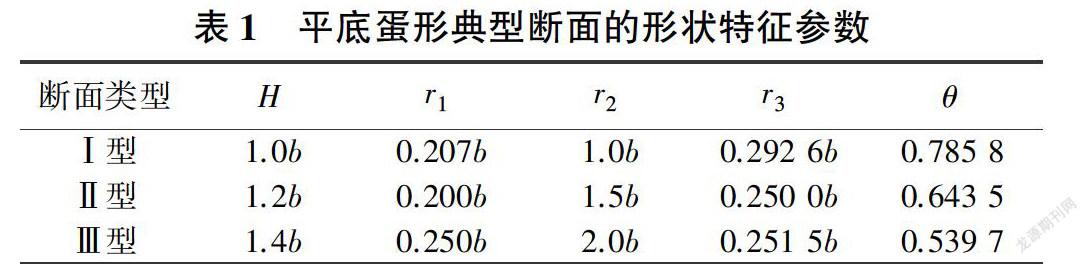
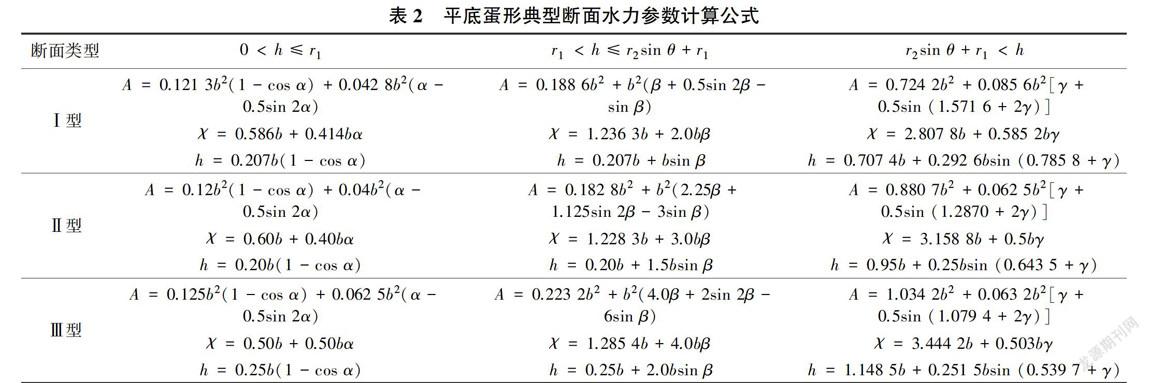
无压隧洞断面高宽比一般在1.0 - 1.5之间,《水工设计手册》[10]给出了3种常用的平底蛋形典型断面形状特征参数,见表1。I型、Ⅱ型和Ⅲ型断面的最大宽度均为6,高宽比分别为1.0、1.2、1.4,中部扇形区域圆弧半径与断面宽度的比值分别为1.0、1.5、2.0。3种断面随着高宽比的增大,断面向“瘦高形”变化,顶拱圆心角越小,越适用于垂直地应力(竖向荷载)大的场合。
3 平底蛋形断面正常水深计算
3.1 平底蛋形断面正常水深的理论计算
平底蛋形断面正常水深的计算采用明渠均匀流基本方程,即
将表2中3种平底蛋形典型断面的水力参数计算公式代人式(4),整理可得不同水深范围的正常水深求解方程。限于篇幅,仅给出I型断面的正常水深求解方程,Ⅱ型、Ⅲ型求解方程类似。
由式(5)可知,平底蛋形典型断面的正常水深方程均为关于圆心角与已知量综合参数的一元方程。式(5)为超越方程,无法直接求解计算,一般通过间接迭代法或试算法求解,计算过程较为复杂。
3.2 平底蛋形典型断面正常水深的直接计算式推求
关于无压隧洞无量纲正常水深x的取值范围,理论上为0≤x≤H/b,在工程实际中,对于x<0.05的较小过流情况,正常水深计算的实际意义不大。同时现行规范[11]规定,无压隧洞应避免运行中出现明满流交替状态,要求顶部净空面积不小于整个隧洞断面面积的15%。经试算求得XI≤0.75、xII≤0.90、xIII≤1.05,无量纲正常水深均位于断面顶拱以下区域内,相应的无量纲综合参数Y1∈[0.040 5,0.477 2]、yII∈[0.040 9.0.541 5]、yⅢ∈[0.038 1,0.608 5].
在x取值范围内以一定的步长值给定一组数值,将其代人式(6)的αβ表达式中,再将求出的αβ值代人式(5),即可求得相应的无量纲综合参数y值。运用Curve Expert软件,对散点(y、x)进行拟合分析,得到无量纲正常水深的直接计算公式。I型断面公式为
4 公式精度分析
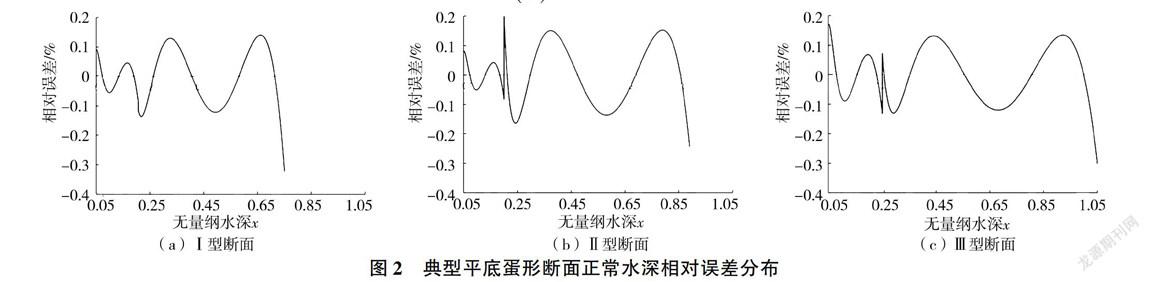
为分析拟合公式的正确性及误差分布情况,以I型断面为例进行精度分析。首先在XI∈[0.05,0.75]的范围内给定不同的x值,由式(6)求出α、β值,再将其代人式(5),求出相应的y值,把y值代人式(7)即可求出x的近似值x,从而计算准确值x的相对误差,同理可得出Ⅱ型和Ⅲ型断面拟合公式(8)、公式(9)的误差分布情况,具体结果见图2。
由图2可知,正常水深直接计算公式在适用范围内的相对误差围绕无量纲水深x呈正负小幅波动,相对误差均较小,大部分区域相对误差在±0.1%之间,最大相对误差不超过0.34%。表明上述正常水深直接计算公式可满足工程需要,是3种平底蛋形典型断面正常水深计算的高精度简便方法。
5 应用举例
某水库泄洪隧洞拟采用平底蛋形断面,断面最大宽度6= 8.4 m,隧洞表面糙率n=0.015.隧洞比降江0.014,设计流量为460 m/s,校核流量为580 m/s,分别计算采用I、Ⅱ、Ⅲ型断面时的隧洞正常水深。
经计算得:采用I型断面时,正常水深数值解分别为4.342、5.362 m,相对误差分别为-0.1 12%、0.122%;采用Ⅱ型断面时,正常水深数值解分别为4.293、5.206m,相对误差分别为-0.074%.-0. 116%:采用Ⅲ型断面时,正常水深数值解分别为4. 311、5.157 m,相对误差分别为0.068%、- 0.083%。可见,拟合公式精度满足工程需要。
6 结论
根据明渠均匀流基本方程,推导了平底蛋形断面的水力要素表达式,研究了其正常水深的计算方法,通过拟合优化计算,给出了3种平底蛋形典型断面正常水深的直接简化计算公式。通过算例验证了正常水深直接计算公式的准确性,与理论值比较,其最大相对误差仅为0.34%。直接计算公式形式简单、计算方便,精度完全满足工程应用要求,便于工程设计应用。
参考文献:
[l] 吕宏兴,裴国霞,杨玲霞,水力学[M].2版,北京:中国农业出版社,2011:6.
[2] 赵延风,刘军,梅淑霞,等,普通城门洞形断面正常水深的近似计算方法[J].武汉大学学报(工学版),2009,42(6):773.
[3] 赵延风,王正中,方兴,等,排灌输水隧洞正常水深的简捷算法[J].排灌机械工程学报,2011,29(6):523-528.
[4] 赵延风,王正中,芦琴,等,马蹄形断面正常水深的直接计算公式[J].水力发电学报,2012,31(1):173-177.
[5] 吕宏兴,辛全才,花立峰,马蹄形過水断面正常水深的迭代计算[J].长江科学院院报,2001,18(3):7-9.
[6]张志昌,贾斌,李若冰,六圆弧蛋形断面正常水深直接计算方法[J].西北农林科技大学学报(自然科学版),2015,43(8):229-234.
[7] 张志昌,贾斌,明渠六圆弧蛋形断面水面线的近似计算[J].应用力学学报,2015,32(3):229-234.
[8]滕凯,蛋形断面隧洞正常水深的简易计算方法[J].长江科学院院报,2013,30( 12):39-42.
[9] 张志昌,贾斌,标准I型四圆弧蛋形断面的水力计算[J].应用力学学报,2015(6):229-234.
[10]索丽生,刘宁,水工设计手册[M].2版,北京:中国水利水电出版社,2011:426.
[11] 中华人民共和国水利部,水工隧洞设计规范:SL279-2016[S].北京:中国水利水电出版社,2016:15.
【责任编辑张华岩】
