层状岩体变形模量参数全过程确定方法研究

赵顺利　杜卫长　朱永和

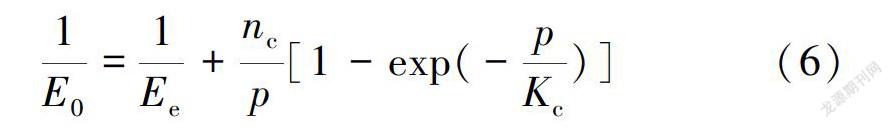
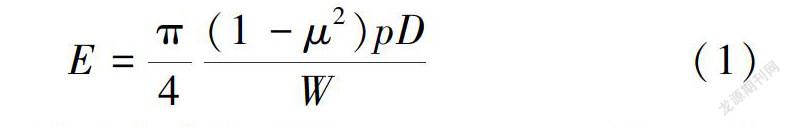
摘要：针对层状岩体现场变形试验中一个综合变形模量指标无法准确反映全过程变形特征的问题，引入自然应变的概念，从单裂隙结构出发，推导了适用于层状岩体结构的压力变形关系曲线解析方程，并进一步建立应力与变形模量的负指数模型。为验证负指数模型的有效性，通过几内亚苏阿皮蒂水利枢纽工程坝址区层状岩体变形试验成果进行验证。研究结果表明，提出的确定层状岩体变形试验全过程变形模量的方法可以高精度拟合试验数据，并可以较好地表达应力与变形模量的非线性关系。

关键词：层状岩体：变形试验;变形模量;自然应变

中图分类号：TV221.2

文献标志码：A

doi：10.3969/j.issn.1000- 1379.2019. 04.019

在水利水电工程中，准确获取岩体的变形特征参数对于保证工程的安全性具有重要意义。目前，获取岩体变形参数的方法较多，总体而言有经验法和现场试验法两类。张占荣等[1]指出经验法作为一种经济实用的方法，可以在现场试验条件受限时，提供可供参考的岩体变形模量值。目前国内外对经验法均有较多的研究，Hoek E开创并发展了地质强度指标（GSI），建立了GSI与岩体变形模量之间的函数关系[2-3].基于GSI的方法得到了广大国内外学者的一致认可[4-5].常用的经验法指标还包括BQ、RQD、波速等[1.6-7]，除了上述单指标方法，目前还提出了基于神经网络的多指标方法[8]。

经验法估算岩体变形模量相对经济便捷，但由于其存在误差难以估计的劣势，因此经验法的工程应用受到了较大的限制，仅适用于初步设计阶段或中小型岩土工程[7]。随着水利水电工程对工程稳定性的分析日趋精细，以及计算机技术、数值方法的迅速发展，对岩体参数的可靠性提出了较高的要求[9].现场试验法依旧是目前最常用的确定岩体变形模量的方法。

在现场试验法中，刚性承压板法是水利水电工程中获取岩体变形参数的一种重要试验方法。但是对于层状岩体而言，鉴于其各层力学性质的复杂性，通常承压板法得到的岩体等效变形模量不能准确反映各个单层的变形性质[9]，更加突出的问题在于，层状岩体的层间结合部位通常存在较多的张开裂隙和软弱夹层，在施加法向应力的过程中，受裂隙和软弱夹层的闭合效应，岩体的变形模量随着法向应力的增大而增大，在只提出一个变形模量综合指标的情况下难以表征层状岩体的变形特征。目前，科研工作者针对层状岩体的问题开展了一定的研究工作。周火明等[IO]通过数值模拟的方法研究了层状岩体变形的尺寸效应。李迪等[11]则创新性地提出分层模量的计算方法。但是已有的研究成果依旧没有提出层状岩体模量随应力增大的理论解析式。

为了解决层状岩体试验中一个综合变形模量指标无法准确反映全过程变形特征的问题，笔者通过引入自然应变的概念，建立了压力p与变形W的负指数模型，提出了适用于层状岩体变形试验全过程变形模量的确定方法。

1 层状岩体变形分析

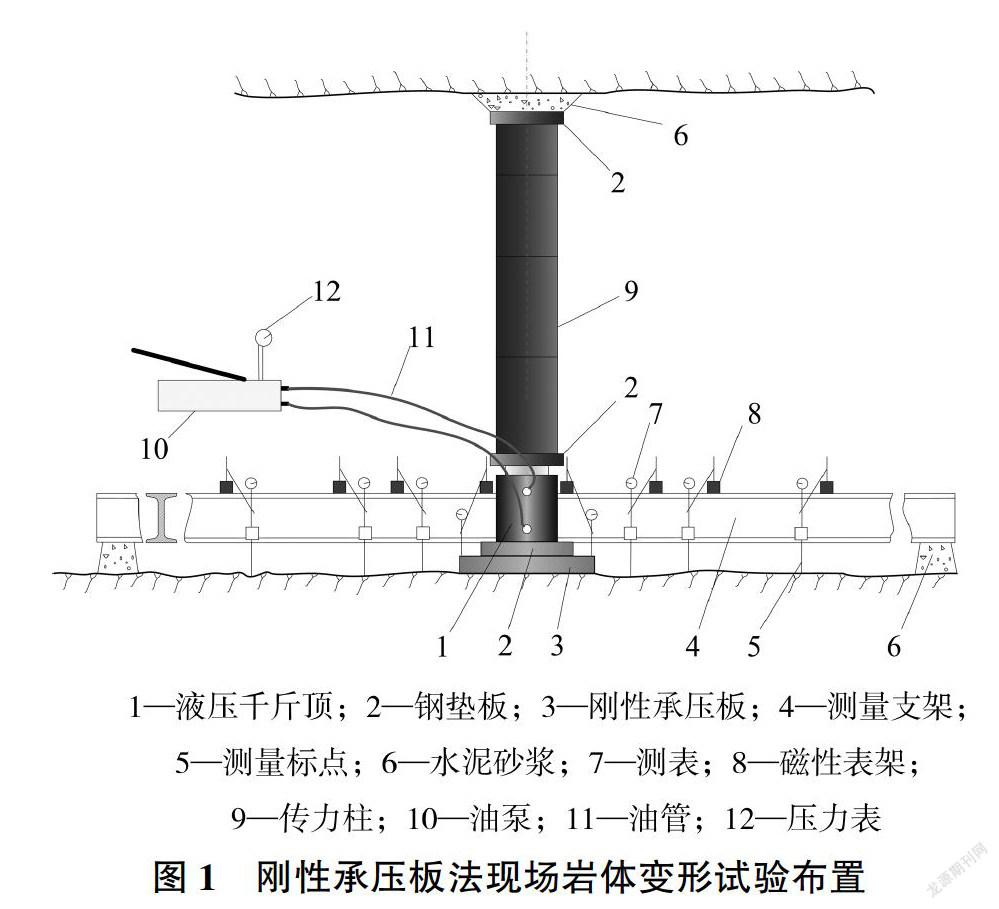
刚性承压板法试验是利用承压板进行岩体变形参数原位测试方法的一种，用千斤顶通过承压板向半无限岩体表面施力测量岩体变形。假定岩体为均匀、连贯、各向同性的半无限弹性体，可按布西涅斯克公式计算岩体的变形参数。具体试验布置如图1所示。

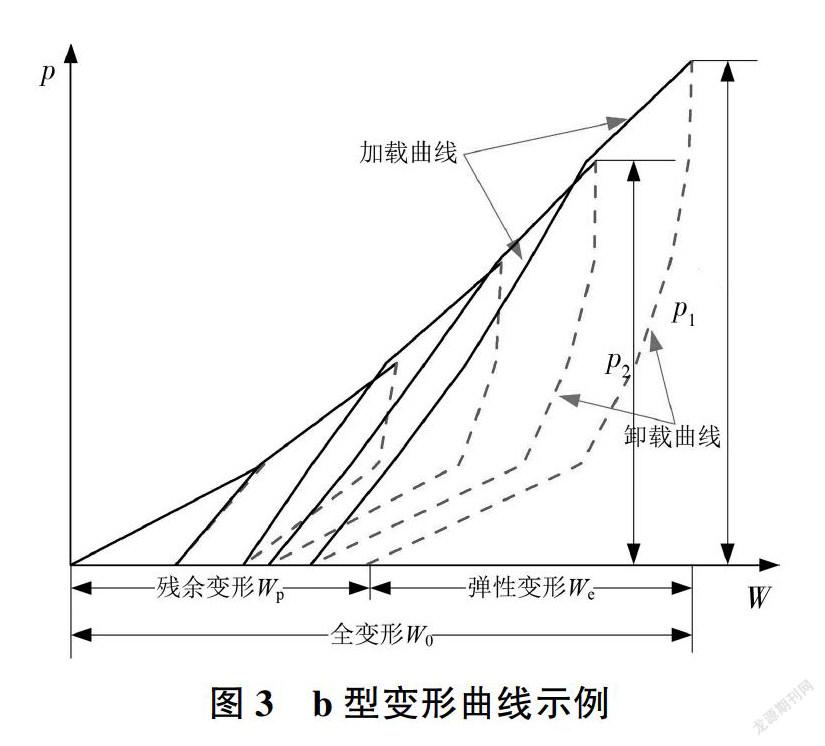
在层状岩体的变形试验中，其层间结合部位通常存在较多张开裂隙和软弱夹层，如图2所示。其压力p与变形W的关系曲线通常为b型，呈现出明显的层间压密特征，典型的曲线类型如图3所示。

在试验成果整理的过程中，依据《水利水电工程岩石试验规程》（ SL264-2001）[12]，此种曲线的变形模量需要分级计算，具体计算公式为

通过式（1）和图3不难发现，随着压力的增大变形模量呈现逐渐增大的趋势。但是具体到设计部门进行工程验算时，不同的工程部位和不同的施工阶段面临的工程应力并不一致，分级计算产生的变形模量难以满足不同工程应力条件的需求，不具有连续性。当采用数值模型进行稳定性分析时.更是难以表达出低应力下的压密特征，在只提供最高应力条件下的变形模量时，通常会造成计算的变形值偏小。

2 层状岩体变形模量确定方法

2.1 单裂隙结构的负指数模型

为解决室内岩石试验中岩石微裂纹压密模型构建问题，彭俊等[13]在参考了单裂隙法向变形规律的基础上，提出了负指数模型，在具体模拟计算过程中得到了较好的应用效果，但主要是通过经验直接提出的，并未阐明模型中参数的物理意义。

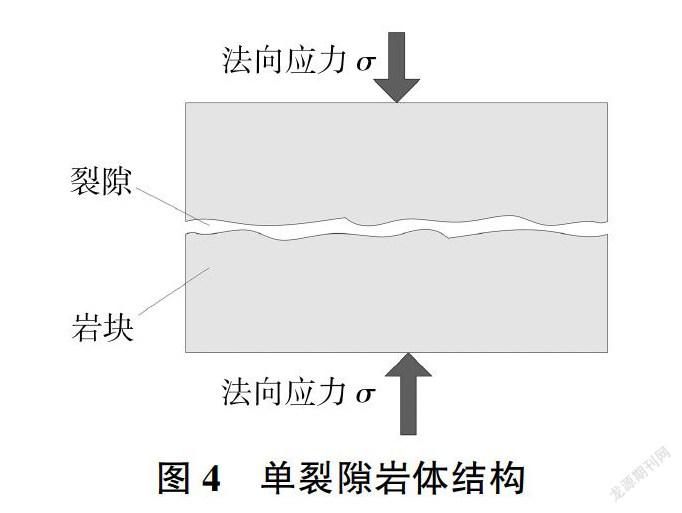
为进一步研究负指数模型的理论适用性和物理力学意义，笔者通过图4的物理力学模型，在文献[14]的基础上引入自然应变的概念，构建了适用于单裂隙结构的负指数模型。

区别于被广泛应用的工程应变εe，自然应变εt能够更精确地反映材料的变形规律，两种应变的表达式分别为[15]式中：L为岩体结构在当前应力状态下的长度;L0为没有应力作用时岩体结构的初始法向长度。

在总结自然应变和工程应变研究的基础上，Freedc16]提出对于法向刚度较小的材料（流体、断层带、裂隙、软土等）不适宜采用公式（2）计算应变。笔者在文献[14]的基础上进一步提出应力刚度比σ/K的概念，其中σ为材料所受法向应力、K为材料的刚度。研究表明，当应力刚度比满足σ/K< 10%时公式（2）和公式（3）可以等效，反之則用公式（3）精确表达材料的变形特性。

通过岩体变形特征分析，其变形主要由高刚度的岩块和低刚度的裂隙、软弱夹层组成。结合图4的单裂隙岩体结构，可以推导出用工程应变εe表达的应力应变关系方程：

通过上述研究可以发现，刚度较高的材料应力应变关系符合线性关系，而低刚度材料的应力应变关系则需要通过负指数模型计算。

2.2 层状岩体的变形模量负指数模型

层状岩体中往往包含较多低刚度材料，为了分析的方便，将低刚度材料综合为一种刚度，高刚度材料应力应变具有线性可加性，同样可以假设为一种综合刚度指标，这样，在保证层状岩体变形性质得到较好表达的基础上，不会增大岩体变形模量模型的复杂性。适用于层状岩体的压力p与变形W的负指数模型为式中：Ee为高刚度材料的弹性模量，层状岩体通常对应于相对完整的岩石结构的模量，在压力变形曲线中对应着直线段模量。

需要特别注意的是，Ee与规范中的弹性模量存在一定的区别，规范中弹性模量按照可恢复的变形进行计算，但是实际卸载过程中，鉴于裂隙、岩石基质耦合过程中的能量损耗等原因，在有限的稳定时间内，弹性变形无法完全恢复，导致按规范计算的弹性变形偏小，对应的弹性模量偏大，式（5）中弹性模量主要与加载过程有关，主要考虑岩体变形的线弹性特性，包含不可恢复的变形，因此计算的弹性模量偏小。

根据式（5）可进一步推导出下式：

具体到试验数据处理时，可根据加载曲线和式（5）确定不同的工程参数，得到层状岩体变形试验的变形模量与工程应力之间的关系，充分考虑层状岩体加载初期的大变形特征，并且可进行编程，便于开展工程稳定性分析。

3 工程实例

利用实际开展的层状岩体现场试验数据进一步验证提出的层状岩体变形模量确定方法的有效性。

3.1 工程概况

几内亚苏阿皮蒂（Souapiti）水利枢纽工程坝址区右岸属于典型的砂岩层状构造，揭露出来的岩性表明砂岩层之间包含遇水易软化的泥质粉砂岩，且层状节理发育。为研究层状砂岩的变形特性，布置了3组（E-1、E-2和E-3）现场岩体变形试验，试验方法采用刚性承压板法，试验区域的地质切面如图5所示。最大法向应力为3.0 MPa，等分5级加载，岩体泊松比μ采用室内试验成果，取0. 25.承压板直径D为50.5cm.测得的压力p与变形W的关系曲线如图6所示。

3.2 變形模量确定

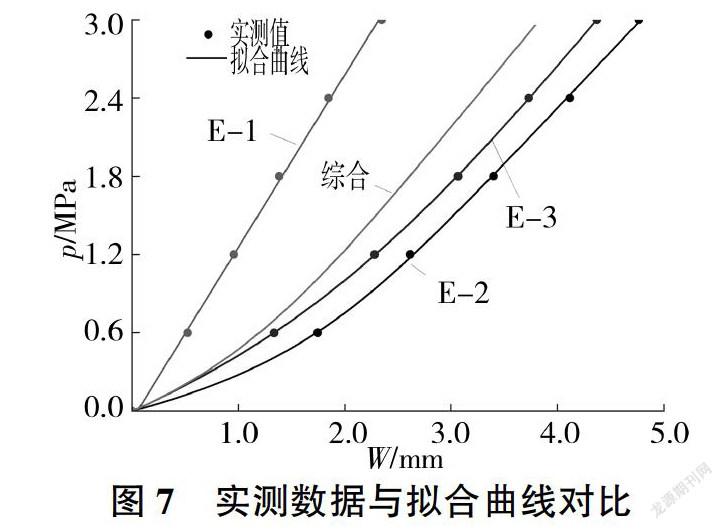
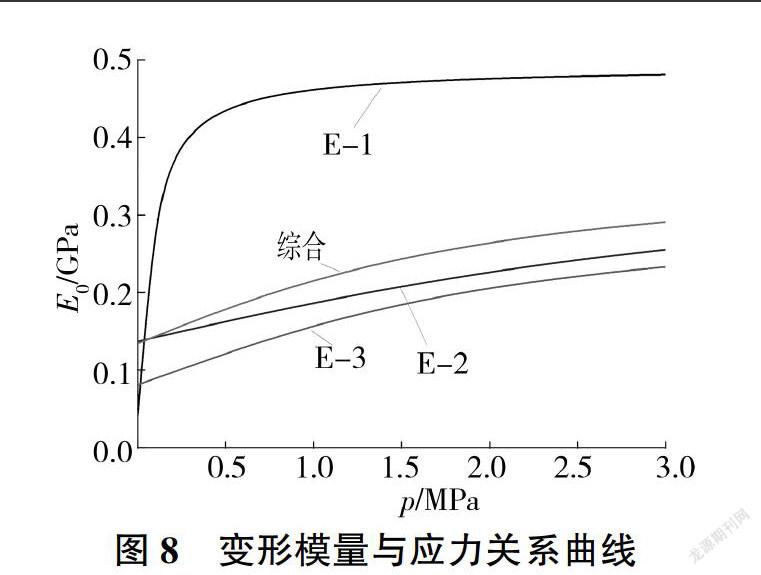
根据式（5），采用MATALB软件进行编程，只保留加载点数据，求得对应的层状岩体变形参数，见表1。表1中的综合指标为3组变形试验结果的综合，综合方法为：将各级同一应力状态下的3组变形值进行平均，平均后的变形值与应力值组成综合意义上的压力变形曲线，通过式（5）进行编程拟合。实测数据与拟合曲线见图7。由表1中的参数可进一步按照式（6）求得应力与变形模量的全过程曲线，如图8所示。由图7、图8不难发现，提出的层状岩体变形模量确定方法可以很好地模拟现场岩体试验的应力变形过程，并且很好地表达变形模量与应力之间的非线性关系。

需要注意的是，负指数模型主要适用于具有明显硬软分层的层状岩体，并且要求岩体在加载过程中没有发生屈服破坏，长期工程实践显示，试验过程中施加的法向应力一般不会造成岩体发生屈服破坏。在模拟其他岩层时，如果出现b型曲线，那么原则上可通过负指数模型进行模拟，如果没有出现典型的b型曲线，负指数模型则不适用，对于不同类型的曲线，通常对应着不同的岩体变形机理，需要探寻适合的连续性方程。

4 结论

通过引入自然应变的概念，推导并建立了适用于层状岩体的确定变形模量的负指数模型。经过研究得到以下结论。

（1）负指数模型可以很好地拟合层状岩体的试验数据，并且可以较好地表达变形模量与应力之间的非线性关系。

（2）负指数模型可以模拟层状岩体的压密特征，并且可进行编程，便于开展工程稳定性分析。

（3）层状岩体变形模量确定方法中的弹性模量与规范中的弹性模量存在一定的区别，按规范计算的弹性模量偏小。

参考文献：

[1] 张占荣，杨艳霜，赵新益，等，岩体变形参数确定的经验方法研究[J].岩石力学与工程学报，2016，35（1）：3195-3202.

[2] HOEK E，BROWN E T.Practical Estimates of Rock MassStrength[ J]. Intemational Journal of Rock Mechanics andMining Sciences， 1997， 34（8）：1165-1186.

[3]HOEK E，DIEDERICHS M S.Empirical Estimation of RockMass Modulus[J].Intemational Joumal of Rock Mechanicsand Mining Sciences， 2006， 43（2）： 203-215.

[4]SONMEZ H，COKCEOCLU C，ULUSAY R.Indirect Deter-mination of the Modulus of Deformation of Rock MassesBased on the CSI System[J].International Journal of RockMechanics and Mining Sciences， 2004， 41（5）：849-857.

[5] 卢书强，许模，基于CSI系统的岩体变形模量取值及应用[J].岩石力学与工程学报，2009，28（增刊1）：2736-2742.

[6] 李维树，黄志鹏，谭新，水电工程岩体变形模量与波速相关性研究及应用[C]//第十一次全国岩石力学与工程学术大会论文集，武汉：湖北科学技术出版社，2010：2727-2733.

[7]宋彦辉，巨广宏，孙苗，岩体波速与坝基岩体变形模量关系[J].岩土力学，2011，32（5）：1507-1512.

[8] 张楠，王亮清，葛云峰，等，基于因子分析的BP神经网络在岩体变形模量预测中的应用[J].工程地质学报，2016，24（1）：87-95.

[9] 熊诗湖，层状岩体变形特性试验研究[D].武汉：长江科学院，2007：4-8.

[10] 周火明，盛谦，陈殊伟，等，层状复合岩体变形试验尺寸效应的数值模拟[J].岩石力学与工程学报，2004，23 （2）：289-292.

[11]李迪，张漫，王志旺，关于层状岩体变形试验的建议方法[J].岩土力学，2006，27（增刊2）：1156-1160.

[12] 中华人民共和国水利部，水利水电工程岩石试验规程：SL264-2001[S].北京：中国水利水电出版社，2001：45-54.

[13] 彭俊，荣冠，周创兵，等，岩石裂纹闭合效应及其定量模型研究[J].岩土力学，2016，37（1）：126-132.

[14] 赵顺利.基于裂纹模型的脆性岩石热一水一力耦合作用研究[D].武汉：武汉理工大学，2017：36-42.

[15] LIU H H， RUTQVIST J，BERRYMAN J G.On the Rela-tionship Between Stress and Elastic Strain for Porous andFractured Rock [J]. International Joumal of RockMechanics and Mining Sciences， 2009， 46（2）：289-296.

[16] FREED A D.Natural strain[ J]. Joumal of EngineeringMaterials and Technology， 1995， 117（4）：379-385.

【责任编辑张华岩】