基于DEM分辨率的侵蚀学坡长尺度效应研究

樊宇　郭伟玲　吴江　土祥　赵令

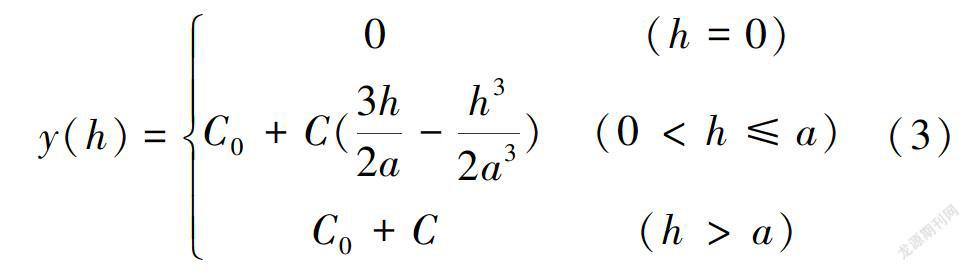
摘要：将DEM分辨率对流域分布式侵蚀学坡长提取的影响分为数据平滑和采样间距两种组分作用形式，选取陕西省安塞县县南沟流域为研究区，探究两种分辨率组分对侵蚀学坡长提取的影响程度以及水平分辨率对侵蚀学坡长空间格局的影响。研究发现，DEM从2.5 m至100 m这一降分辨率过程中，坡长平均值呈现对数递增的趋势。对2.5 m至100 m分辨率DEM提取坡长进行不同分辨率组分作用研究发现，用不同分辨率DEM提取侵蚀学坡长时采样间距对坡长的影响作用均大于数据平滑的。对10 m至100m水平分辨率DEM提取的坡长通过半变异函数分析其空间格局变化情况，结果表明：坡长变异函数采用球状模型拟合效果最佳，并且随着分辨率降低，坡长的空间结构总体变异和随机变异减小，空间相关性范围增大。

关键词：侵蚀学坡长;数据平滑;采样间距;空间格局;半变异函数;安塞县县南沟流域

中图分类号：S157.1

文献标志码：A

doi：10.3969/j.issn. 1000-1379.2019. 04.017

地形是土壤侵蚀的主要影响因子[1]，而坡度和坡长是影响土壤侵蚀的主要地形指标[2]。在宏观尺度上的土壤侵蚀预报和分析中，坡度与坡长通常基于中低分辨率数字高程模型（ DEM）提取[3]。本文所采用的坡长概念不同于地貌学坡长和水文学坡长，而是指地表径流原点沿流水线到坡度减小至有沉积出现的地方，或者到一个明显沟渠之间的水平距离[1].即土壤侵蚀学坡长。国内外一些研究者对坡长的尺度效应问题进行了研究：C.D.Stefano等[4]研究表明，坡长中值对DEM栅格尺寸有一定的依赖性：N.R.Prodhan等[5]研究认为在进行降雨径流模拟时，计算低分辨率DEM上的坡长时需要考虑DEM分辨率带来的坡长尺度效应问题：张宏鸣等[6]研究表明，坡长提取精度随分辨率降低而降低，计算误差明显增大：郭伟玲等[7]对坡长尺度效应进行了研究，发现随DEM分辨率降低，坡面中下部的坡长发生扩张，因此DEM对地表细部特征的表达能力将逐渐减弱，也不能为区域尺度水文和土壤侵蚀等模拟计算提供有效的数据支持[8-9]。目前对于坡度与DEM分辨率关系的研究较多[9-10]，而DEM分辨率对分布式土壤侵蚀学坡长（简称分布式坡长）影响的研究相对较少[11]。

D.M.Wolock等[12]研究认为，DEM采样间距（即栅格尺寸）和数据平滑作用对坡度提取的影响是不同的。因此，研究DEM分辨率对地形因子的影响，可以从采样间距和DEM建立或处理过程中的数据平滑作用两方面来认识。为此，笔者以陕西省安塞县县南沟流域为研究区，对分布式坡长均值随DEM分辨率的变化规律及其空间格局变化进行分析，重点研究不同分辨率组分对分布式坡长提取的影响程度。

1 研究方法

1.1 研究区概况

选取沟谷发育充分、地表形态复杂且水土流失严重的黄土丘陵沟壑区典型小流域陕西省安塞县县南沟流域作为研究区域。研究区位于东经lO9°12′-109°21′、北纬36°4°-36°45′，海拔990-1 440 m.平均坡角25°，平均坡长115 m。

1.2 研究方法

为了表现分辨率的两种不同组分对坡长提取的影响，采用具有统一定位基础的县南沟1：10 000比例尺的数字线画图（DLG）数据，通过ANUDEM软件插值生成两组水文地貌关系正确的DEM数据集（HC -DEM） [13-14]，通过LS—TOOL工具，坡度截断因子设置为0.7和0.5.沟道截断河网阈值设置为50 000 m2。采用基于坡度的多流向算法来提取多流向的流域分布式坡长【6]。

数据集1：基于县南沟1：10 000比例尺的DLG数据，通过ANUDEM软件多次插值生成2.5 m栅格大小、5-100 m分辨率、间隔Sm的DEM数据用于提取坡长，视为不同栅格尺寸且不同平滑程度的DEM数据，进行DEM分辨率对坡长提取的总体效应研究，提取的坡长命名为len2_5～lenl00。

数据集2：将数据集1的DEM统一通过双线性重采样方法生成2.5 m栅格大小的DEM.即為相同栅格尺寸不同分辨率的DEM，用于分析数据平滑作用对坡长的影响，提取的坡长命名为len2_5r - lenlOOr。

数据集1用于探讨分辨率总效应对坡长的影响，数据集2用于分析数据平滑对坡长的影响，将数据集2与数据集1中对应的相同平滑程度的DEM提取的坡长进行对比分析，可以探讨采样间距对坡长提取的影响。

1.3 分辨率组分作用研究

将DEM分辨率对坡长提取的影响分为数据平滑效应和采样间距效应，探讨不同分辨率DEM提取的坡长之间的衰变程度。对数据集1和数据集2的平均坡长进行统计和运算的公式为

1.4 半变异函数

数字地形分析中，根据经典统计学可以对各种地形参数的均值、标准差等进行统计来获得地形地貌分布特征，但只能概括性地描述地貌大致特征，对一些局部特征不能有效地反映[15]。地统计学注重变量因子的空间过程及其空间自相关性分布，是分析地形因子空间特征及其变异规律的有效方法[16]。当空间点X变化时，区域变化量Z（X）在X轴方向上的变异函数记为y（x，h）：

y（x，h）=11 2Var [Z（x）-Z（x+h）]2 （2）式中：x为空间坐标。

变异函数基台值模型分为纯块金效应模型、球状模型、指数模型、高斯模型4种[17].通过对10 m分辨率坡长数据进行分析，发现球状模型的残差平方和（RSS）最小，决定系数（R2）最大，所以选用球状模型作为坡长变异函数的拟合模型，其一般表达式为

2 结果分析

2.1 DEM分辨率与平均坡长的关系

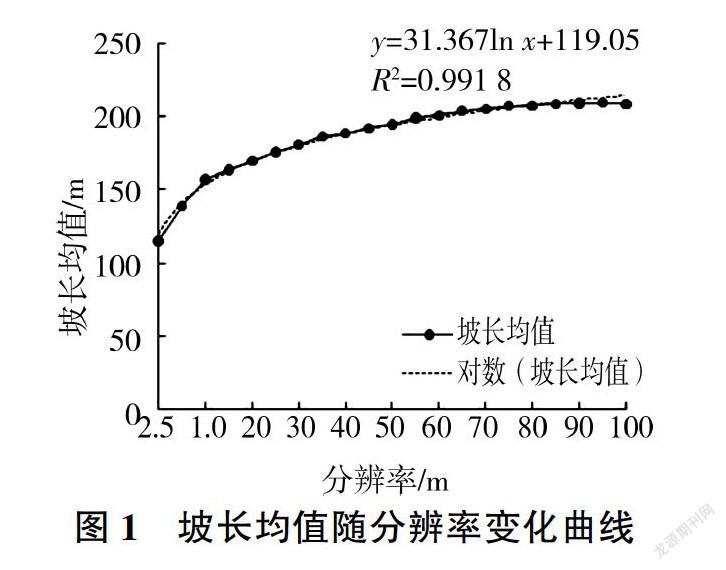
从分析数据集1中2.5 m栅格大小、5-100 m分辨率、间隔Sm的DEM上提取的坡长平均值来看（图1），坡长均值随分辨率的降低呈对数递增趋势，其对数相关关系为：y= 31. 367lnx+119. 05（ R=0. 991 8）。从流域分布式坡长的截断方式[18]来看，其原因可能是2.5 - 100 m分辨率DEM的沟道衰减大于坡度衰减，沟道细节的消失导致原先两个汇水面融合成一个大的汇水面，使得坡长均值增大。

2.2 DEM数据平滑和采样间距与平均坡长的关系

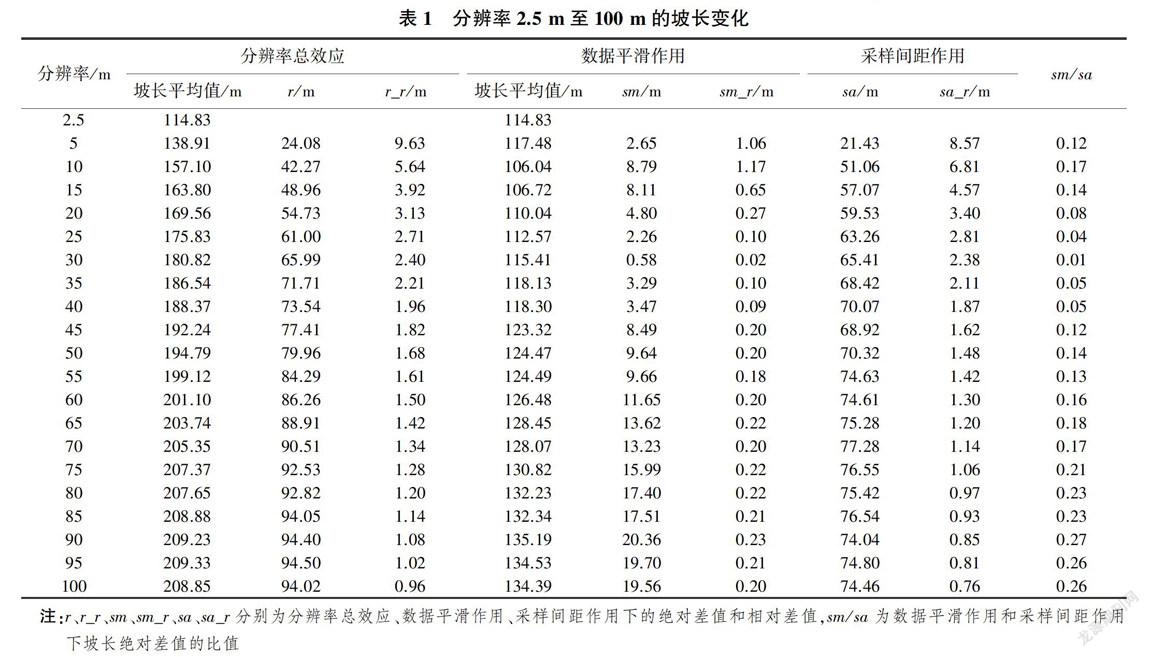
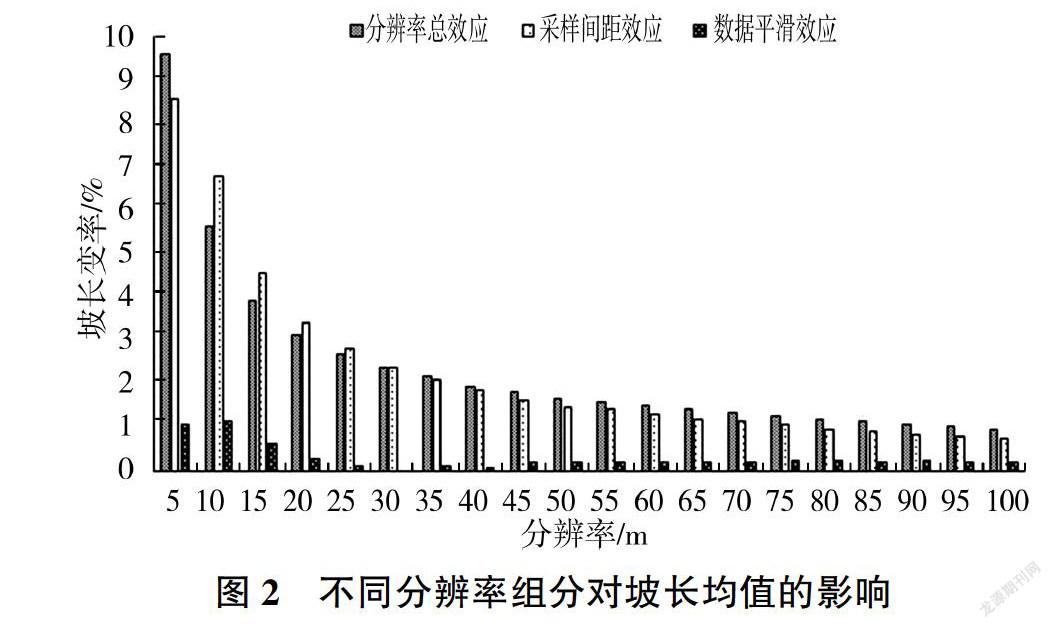
为了定量分析分辨率的两种组分作用对平均坡长的影响，以研究区最佳分辨率2.5 m DEM[13]提取的坡长为真值，利用式（1）计算样区数据集1和数据集2的平均坡长，结果见表1和图2。

通过表1和图2中各个分辨率与最佳分辨率提取的坡长均值的差值以及变率来探讨分辨率总效应、数据平滑效应和采样间距作用下平均坡长的变化情况，发现随着分辨率的降低，各分辨率组分的坡长均值的绝对差值（r、sm、sa）都逐渐增大，采样间距作用的坡长绝对差值比平滑作用的增幅大，说明采样间距对坡长提取的影响大于地形平滑作用。二者变化趋势相同，都随着分辨率的降低而增大，且增幅逐渐趋于平缓。

通过对比各分辨率组分的坡长均值变率，发现随着分辨率降低，各个组分对坡长影响的相对差值（ r_r、sm一r、sa_r）逐渐变小并趋于平稳，即分辨率对坡长衰减的影响程度逐渐变小。从数据平滑变率和采样间距变率的比值来看，随着分辨率的降低，采样间距作用对坡长的影响逐渐变大，而数据平滑则相反。二者比值均小于1，说明在各分辨率条件下采样间距作用对坡长的影响均大于数据平滑作用的。

2.3 分布式坡长空间变异结构分析

2.3.1 10 m分辨率坡长变异函数分析

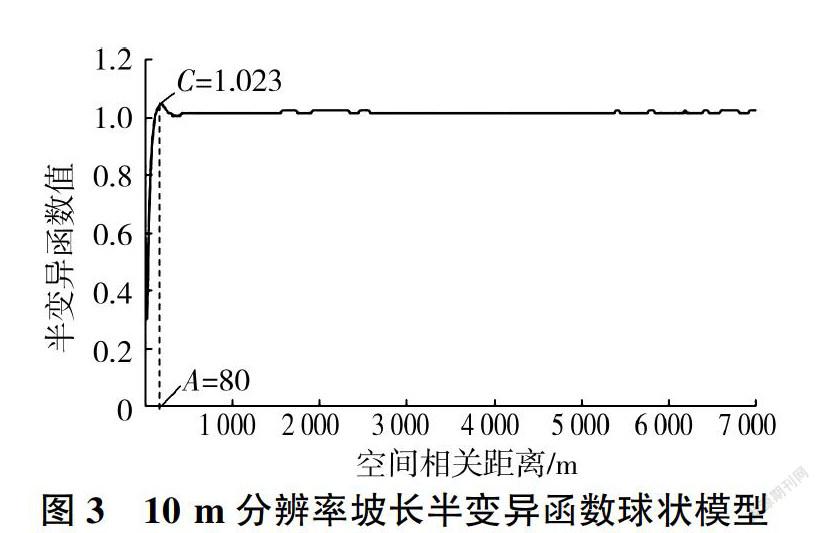
考虑数据精度和计算处理效率等因素，以相对较为精细的10 m分辨率坡长数据为例，对其进行半变异函数计算，结果显示球状模型的残差平方和最小（0.036 9），决定系数最大（0.967），所以10 m分辨率坡长的最佳理论模型为球状模型。根据图3球状模型（10 m分辨率坡长）可知，变程为80 m（即10 m分辨率）坡长的最大空间相关距离为80 m，块金系数为0.064，表明相邻的两个坡长之间具有强烈的空间相关性。

2.3.2 不同分辨率坡长变异函数分析

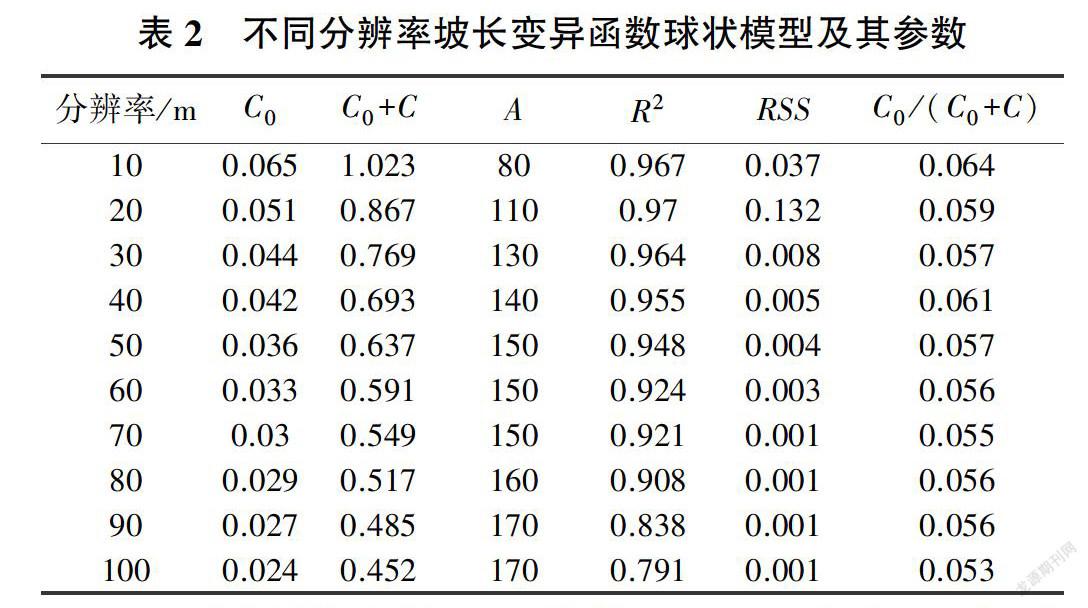
半变异函数包含的参数有块金值C0、基台值C0+C、变程A、决定系数R、残差平方和RSS、块金系数CO/（ CO+C），不同分辨率的坡长半变异函数的参数见表2。

不同分辨率的块金系数均在0.060左右，且随分辨率降低有减小的趋势，说明不同分辨率的坡长结构都具有强烈的空间相关性。基台值代表空间总变异，块金值代表随机变异，它们都随着分辨率的降低而迅速减小，而变程则呈现增大趋势，说明坡长结构的空间变异程度和变异范围受分辨率影响较大，且影响力随着分辨率增大而逐渐稳定。

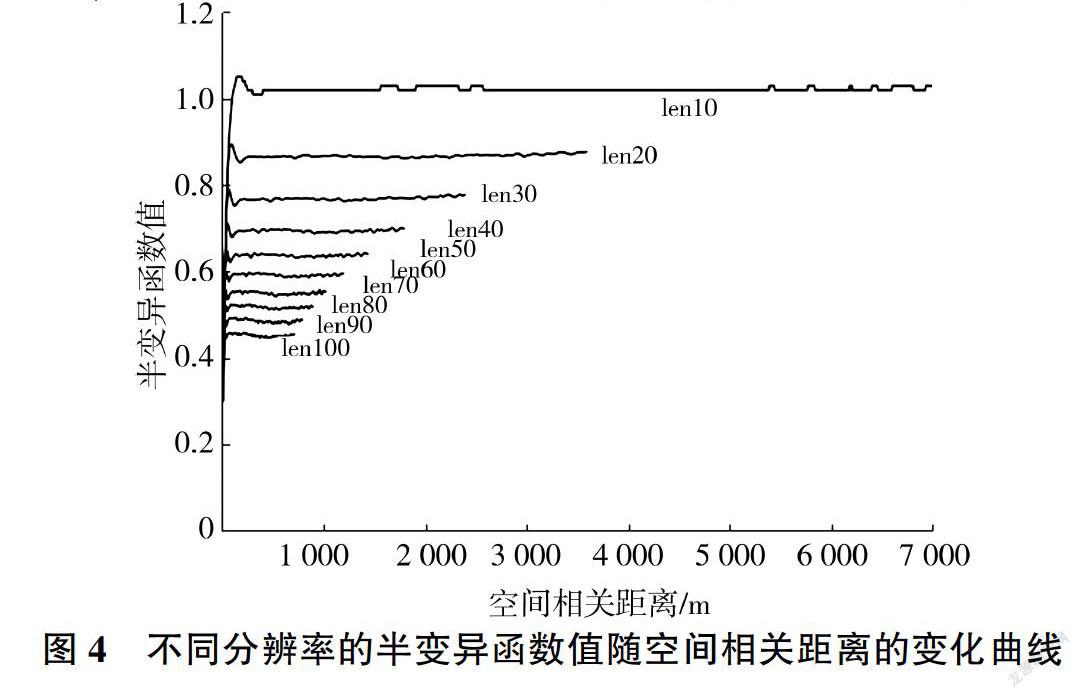
不同分辨率的半变异函数值随空间相关距离的变化曲线见图4，可以看出，距离和半变异函数值均随分辨率的降低而减小。由表2可以看出，块金值和基台值也有相同的变化规律，说明低分辨率坡长结构的空间总变异和随机变异较小，高分辨率坡长结构性好，对坡长结构的描述能力比低分辨率要细腻（见图5），原因是分辨率降低导致DEM对地形的制图综合作用增强，使得沟道等细节表达被概括，其上提取的坡长结构也随之发生变化，导致半变异函数值减小，反映坡长结构的能力也随之降低。坡长变程随分辨率降低而增大，表明空间相关性的范围随分辨率降低而增大。

3 结论

（1）分析从2.5 - 100 m分辨率DEM上提取的坡长均值随分辨率变化情况发现，坡长平均值呈现对数递增的趋势，其相关关系为y= 31. 367lnx+119. 05（R2 =0.991 8），随着DEM分辨率的降低，由于侵蚀学坡长是以坡度和沟道作为截断因子，而不同分辨率对坡度和沟道提取的影响不同，因此产生坡长截断因子的尺度效应问题，从而导致坡长随分辨率发生变化。

（2）将DEM分辨率划分为数据平滑效应和采样间距效应两种组分，分析其对2.5 - 100 m分辨率DEM上提取坡长的影响。研究发现，两种组分对坡长影响趋势相同，坡长均随分辨率的降低而增大，且增幅逐渐趋于稳定，但采样间距对不同分辨率DEM提取的坡长影响大于数据平滑作用。

（3）对10 -100 m不同分辨率坡长空间结构进行半变异函数拟合分析，结果表明坡长值的变异函数采用球状模型时的模拟效果最佳且空间相关性较强。随着分辨率降低，坡長变异函数模型的基台值和块金值相应快速减小并达到稳定，说明坡长的空间结构变异和随机变异逐渐减小，分辨率对空间整体变异和空间相关性作用范围的影响力随着分辨率的降低而减弱并趋于稳定。

在DEM分辨率对坡长提取的影响研究中，平均坡长值随分辨率降低呈现出对数递增的趋势，其原因是否由分布式坡长的两种截断方式随分辨率变化对坡长截断计算的影响程度不同导致的，还有待进一步论证。本文关于DEM分辨率和不同分辨率组分对坡长提取影响的研究，只选择典型的黄土丘陵沟壑区县南沟流域作为研究区，而在其他地形地貌条件下的变化表现以及如何量化，还需进一步研究。

参考文献：

[1] SMITH D D，WISCHMEIER W H.Factors Affecting Sheetand Rill Erosion[ J]. Transactions American CeophysicalUnion，1957，38（6）：889-896.

[2]LIU B，ZHANC K L，XIE Y.An Empirical Soil Loss Equa-tion[ C]//Proceedings of the 12th International Soil Conser-vation Organization Conference. Beijing： Tsinghua UniversityPress，2002：143-149.

[3]程琳，杨勤科，谢红霞，等，基于CIS和CSLE的陕西省土壤侵蚀定量评价方法研究[J].水土保持学报，2009， 23（5）：61-66.

[4] STEFANO C D， FERRO V， PORTO P.Length Slope Fac-torsfor Applying the Revised Universal Soil Loss Equation atBasin Scale in Southem Italy[J].Joumal of Agricultural En-gineering Research， 2000， 75（4）：349- 364.

[5] PRADHAN N R， OCDEN F L，TACHIKAWA Y， et al.Scaling of Slope， Upslope Area and Soil Water Deficit： Im-plications for Transferability and Regionalization in Topo-graphic Index Modeling[J].Water Resources Research，2008，44（ 12）：57-76.

[6] 张宏鸣，杨勤科，李锐，等，流域分布式侵蚀学坡长的估算方法研究[J].水利学报，2012，43（4）：437-444.

[7] 郭伟玲，杨勤科，程琳，等，区域土壤侵蚀定量评价中的坡长因子尺度变换方法[J].中国水土保持科学，2010，8（5）：73-78.

[8] 汤国安，赵牡丹，李天文，等.DEM提取黄土高原地面坡度的不确定性[J].地理学报，2003，58（6）：824-830.

[9] 刘新华，杨勤科，中国地形起伏度的提取及在水土流失定量评价中的应用[J].水土保持通报，2001，21（1）：57-59.

[10]CAO J.Resolution and Accuracyof Terrain Representationby Crid Dems at a Micro-Scale[J].International Joumal ofCeographical Information Systems， 1997， 11（2）：199-212.

[11]杨勤科，郭偉玲，张宏鸣，等，基于DEM的流域坡度坡长因子计算方法研究初报[J].水土保持通报，2010，30（2）：203-206.

[12]WOLOCK D M， MCCABE G J.Differences in TopographicCharacteristics Computed from lOO-and lOOO-m ResolutionDigital Elevation Model Data[J].Hydrological Processes，2000.14（6）：987-1002.

[13]张彩霞，杨勤科，段建军，高分辨率数字高程模型的构建方法[J].水利学报，2006，37（8）：1009-1014.

[14]杨勤科，MCVICAR T，VAN NIEL T G，等，用ANUDEM建立水文地貌关系正确DEM的方法研究[J].测绘科学，2006，31（6）：155-157.

[15]周启鸣，刘学军，数字地形分析[M].北京：科学出版社，2006：44-65.

[16]WEBSTER R.Quantitative Spatial Analysis of Soil in the Field[M].New York： Springer， 1985： 1-70.

[17]王军，傅伯杰，邱扬，等，黄土丘陵小流域土壤水分的时空变异特征：半变异函数[J].地理学报，2000，1（4）：428-438.

[18]张宏鸣，杨勤科，王猛，等，沟道截断对分布式土壤侵蚀学坡长提取的影响[J].水利学报，2017，48（5）：568-575

【责任编辑张华兴】