向学生揭开动量守恒定律矢量性的面纱

李帖

摘要：本文以动量守恒中一动碰一静以及两个运动的物体相碰撞为基础，结合变式讨论及具化的情景分析为基础，探讨了为学生指明表达式具有矢量含性的方法，同时也改进了验证动量守恒定律实验中的表达形式。

关键词：动量守恒定律；矢量性

在进行动量守恒定律的教学时，学生不能很好的理解表达式的矢量性，为了让学生能够较好的理解表达式的矢量性以及由此 所带来的丰富性，特做了一点尝试。

初探：一动碰一静

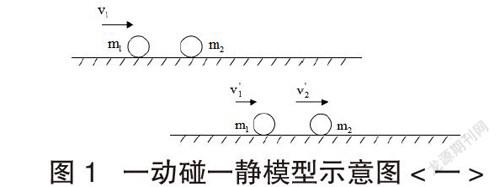
图1 一动碰一静模型示意图<一>

如图1所示，对两个小球所组成的系统，由动量守恒定律以及机械能守恒定律可得：

① ②

①②两式整理，可得：

③ ④

④式比③式，可得： ⑤

将⑤代入①，可得： ⑥ 和 ⑦

可在此处，因为图1以及①所有的字母前均为“+”号，易让学生认为该式所表达的是一动碰一静并且碰后同向的情景，不能很好的理解该式的矢量性、一般性。为此，列出一动碰一静，运动物体碰后反向之情景的表达式做以对比。

图2 一动碰一静示意图<二>

如图2所示，对两个小球所组成的系统，由动量守恒定律以及机械能守恒定律可得：

①’ ②’

①’②’两式整理，可得：

③’ ④’

④’比③’，可得： ⑤’

將⑤’代入①’，可得： ⑥’和 ⑦’

对比⑤和⑤’，不难发现，两式具有相同的形式，且表达式中前的正负号与①或①’中前的正负号相同。稍作提升，便使学生可以理解表达式中的速度是矢量的含义，尤其是的矢量意义为最。

对比⑥和⑥’也能发现：两式中均表示速度大小，方向已在①和①’予以呈现。正因如此，便可将①及⑥视作矢量表达式，①’及其结果⑥’所表达的无非是，即质量轻的物体去碰质量大的物体的情景。

⑦和⑦’表达的均为的大小，其方向一定与的方向相同，故⑦和⑦’表达形式完全相同。

同时，在此也有一个意外的小发现。

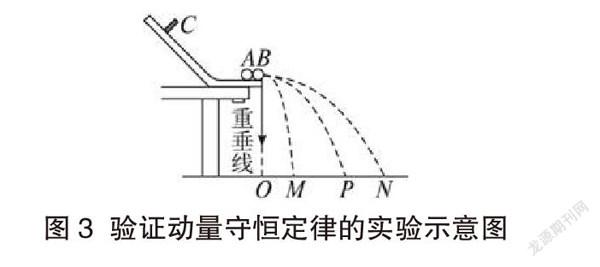
在如图3所示的以完全弹性碰撞为背景设计的验证动量守恒的经典实验中，若以①为依据，则根据小球下落后平抛运动的时间相等，可将其变形为：，最终需要验证的表达式为：。若以①、②两式推出的⑤为依据，可将其变形为，最终需要验证的表达式就变为：，不难看出此表达式更简单，且与两小球的质量无关。

图3 验证动量守恒定律的实验示意图

再探：运动物体相碰撞

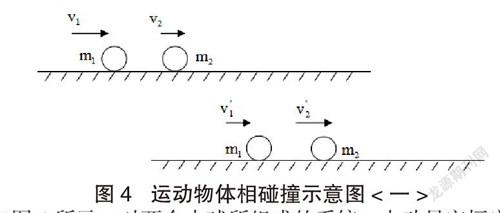
图4 运动物体相碰撞示意图<一>

如图4所示，对两个小球所组成的系统，由动量守恒定律以及机械能守恒定律可得：

⑧ ⑨

⑧⑨两式整理，解得：

⑩ k

同样，在此处，因为图4及⑧前均为“+”号，易让人认为该式所表达的是碰前两物体同向，碰后两物体也同向的情景，不能很好的理解该式的矢量性、一般性。为此，列出碰前两物体反向，碰后两物体均反向之情景的表达式做以对比。

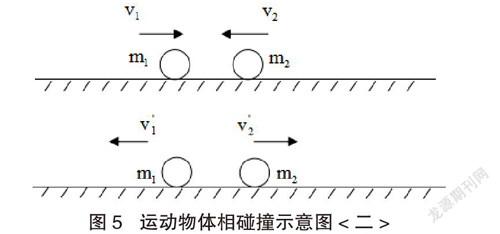
图5 运动物体相碰撞示意图<二>

如图5所示，对两个小球所组成的系统，由动量守恒定律以及机械能守恒定律可得：

⑧’ ⑨’

⑧’⑨’两式整理，解得：

⑩’ k’

图4、图5两例，可仿照图1、图2两例的方式进行分析，从而提升学生对表达式矢量性的认识。

附例题一道，加强学生的认识。

例.如图4所示，两个刚性小球，相向而行，其中m1=2kg，，m2=3kg，，求两小球的碰后速度。

解法一：

按照—的思路完成，以的方向为正方向，有：

解法二：

按照⑧’—k’的思路完成，以的方向为正方向，有：

由此可看到，因⑧式具有矢量性的特点，使得⑧—k的解答过程有了一般性和广泛性。

简单的感悟

通过这两种基本情景的讨论、变式论证以及实例展示，学生们终于充分的理解了依据动量守恒定律所列得的表达式的矢量性以及由此所带来的丰富含义，也使得学生在进行相关讨论时，能够顺利的理解表达式的矢量含义！