铁路大跨度连续梁-拱组合桥拱梁合理刚度比研究

鲁昭 田世宽

摘要：文章结合国内关于连续梁-拱组合结构桥刚梁柔拱、柔梁刚拱和刚梁刚拱的概念，以国内某高速铁路（90+180+90） m连续梁-拱组合结构桥为例，分析了不同拱梁刚度比对结构关键受力部位内力、应力、活载挠度、拱肋稳定性的影响，提出了大跨度连续梁-拱组合结构桥合理拱梁刚度比的取值范围，可为类似桥梁的设计和科研提供经验借鉴。

关键词：连续梁拱;刚度比;稳定性;合理范围;研究

Combining the domestic concept about the rigid beam flexible arch，soft beam rigid arch and rigid beam rigid arch of continuous beamarch combination structure bridge，and with a domestic highspeed railway （90+180+90）m continuous beamarch combination structure bridge as the example，this article analyzes the effects of different arch beam stiffness ratio on the internal force，stress，live load deflection and arch rib stability of key structural members，and proposes the value range for reasonable arch beam stiffness ratio of largespan continuous beamarch combination structure bridge，which can provide the experience reference for the design and research of similar bridges.

Continuous beam arch;Stiffness ratio;Stability;Reasonable range;Research

0 引言

连续梁-拱组合桥是对传统拱桥的发展，它将大跨度连续梁和拱两种结构有机地组合在一起，与同跨度连续梁相比，降低了主梁的高度[1]。连续梁拱桥是由拱肋、吊杆以及预应力混凝土梁等共同组合承受荷载的桥梁结构。这种结构利用主梁的预压力来平衡拱肋对主梁的水平推力，一方面使梁拱共同承受荷载，从整体上节约材料;另一方面拱是以承受压力为主的构件，具有竖向刚度大的特点，形成组合结构以后，在竖向荷载作用下，大部分竖向力通过吊杆传到拱肋上，再由拱肋直接传到主梁根部，因此使主梁跨中及根部弯矩显著减小。作为梁拱组合结构桥梁，在恒载及活载作用下梁和拱两者受力如何分配与拱和梁的刚度比密切相关。

1 拱梁刚度比的分类及计算办法

铁路大跨度连续梁-拱组合结构桥的拱肋一般采用钢管混凝土哑铃型截面，连续梁为预应力混凝土变截面。为了使拱与梁的刚度具有可比性，拱肋的刚度根据[2]《钢管混凝土拱桥技术规程》（GB 50923-2013），可以将钢管混凝土拱肋换算成混凝土等效截面，具体公式[3]如下：

文献[3]认为梁拱组合体系根据拱肋与主梁相对抗弯刚度的大小可分为刚梁柔拱、柔梁刚拱和刚梁刚拱三种：

（1）当（E拱·I拱）/（E梁·I梁）<1/80时，认为拱的抗弯刚度远小于梁的抗弯刚度，不承受弯矩，仅承受轴向压力，弯矩全部由梁承担，这种形式称为刚梁柔拱。

（2）当（E拱·I拱）/（E梁·I梁）>80时，认为梁的抗弯刚度远小于拱的抗弯刚度，即梁不承受弯矩，仅承受水平推力，弯矩全部由拱承担，这种形式称为柔梁刚拱。

（3）当（E拱·I拱）/（E梁·I梁）在1/80～80时，梁和拱均具有一定刚度，共同承受荷载，梁为拉弯构件，拱为压弯构件，弯矩由梁拱按刚度分担，称为刚梁刚拱。

《铁路桥涵设计基本规范》（TB10002.1-2005）[4]中，第5.2.12条规定为：“系杆拱桥跨结构如其拱肋截面刚度与系梁截面刚度的比值<1/80～1/100，拱肋可视为仅承受轴向压力的柔性拱肋;如两截面刚度比值>80～100时，系梁可视为仅承受轴向拉力的系杆，此时拱与梁在连接处可视为铰接。”

从表述上看，以上两篇文献对于刚梁柔拱、柔梁刚拱范围的界定基本一致。

2 拱梁刚度比对结构关键部位内力的影响

为了用具体数据来说明拱梁刚度比对结构的影响，现以国内某高速铁路主跨（90+180+80） m连续梁-拱组合结构桥为例进行研究。本桥施工采用先悬臂浇筑梁体，待全桥合龙后在桥面上搭设支架安装拱肋。计算采用大型通用有限元计算软件Midas Civil进行全桥建模，模型中吊杆采用只受拉桁架单元，拱肋及系杆均采用空间梁单元。计算模型如图1所示。

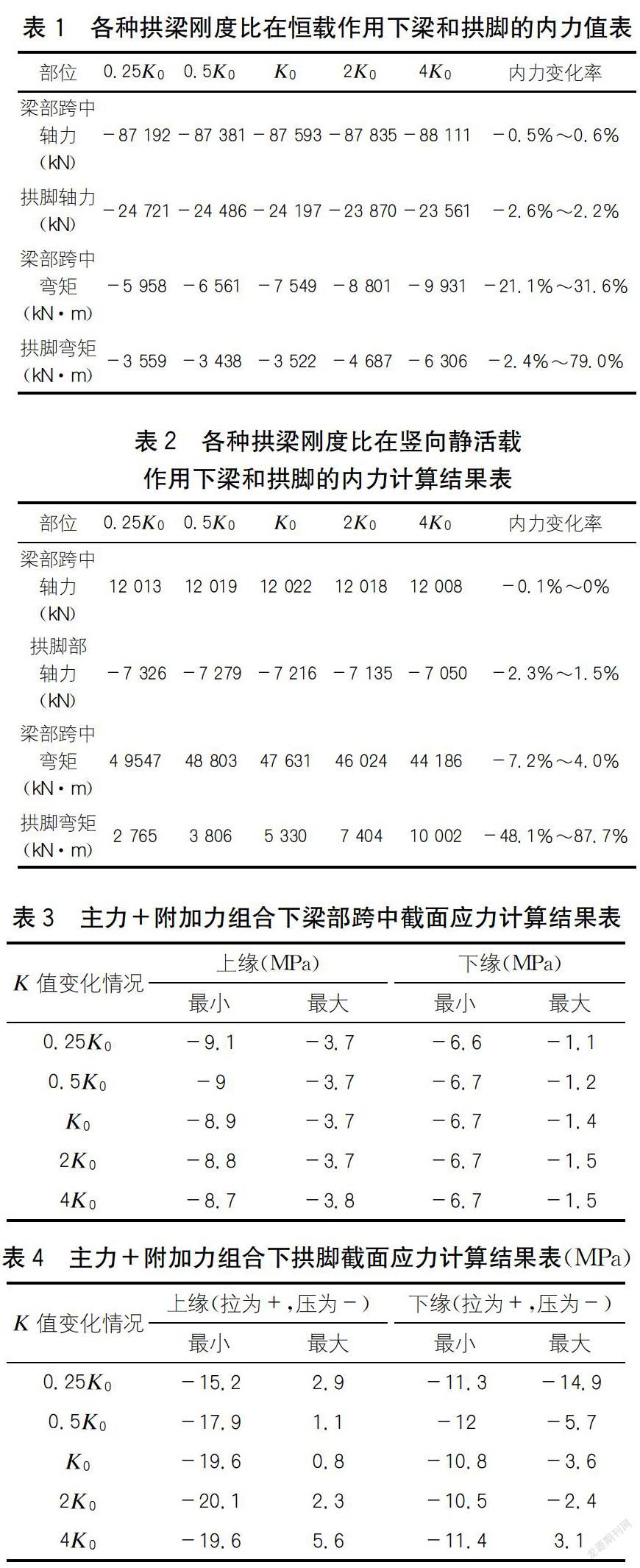
由于连续梁-拱组合桥主梁刚度一般较大，所以不會出现（E拱·I拱）/（E梁·I梁）>80成为柔梁刚拱的情况。借鉴国内已建成部分连续梁拱桥梁拱刚度比的经验，可将钢管混凝土拱的竖向刚度基数暂定为预应力混凝土梁等效竖向刚度的K0=1/25。在保持拱梁的截面面积都不变的情况下，一方面将拱肋的刚度扩大至2K0、4K0;另一方面将拱肋的刚度缩小至0.5K0、0.25K0。同时研究拱肋与梁的刚度比变化对连续梁-拱组合结构桥内力的影响，即研究拱梁刚度比为1/100、1/50、1/25、1/12.5、1/6.25五种情况下，在恒载（含预应力）、竖向静活载作用下梁部跨中、拱脚这两个关键部位的内力变化情况（分别见表1和表2）。其中轴力单位为kN，受拉为“+”，受压为“-”;弯矩单位为kN·m，下缘受拉为“+”，上缘受拉为“-”。

从表1可知：在恒载作用下拱梁刚度比K值从0.25K0变化至4K0，即拱梁刚度比在1/100～1/6.25之间变化时梁部跨中和拱脚的轴力范围<3%，变化范围较小。梁部跨中负弯矩随着K值的增大而增大，且变化趋势较明显，此负弯矩主要由预应力钢束的效应产生。负弯矩变化的主要原因是随着拱的刚度增加，梁体分担自重和二期恒载产生的正弯矩逐步减小，并向拱部转移，因此梁的跨中负弯矩的绝对值随K值的增大而增大，拱脚的弯矩随K值的增大而增大。

从表2可知：在活载作用下拱梁刚度比K值从0.25K0变化至4K0，即拱梁刚度比在1/100～1/6.25之间变化时，梁部跨中和拱脚的轴力范围<3%，变化趋势与恒载作用相近，变化范围较小。梁部跨中正弯矩随着K值的增大而减小但是变化不明显，变化率<8%;拱脚处的弯矩随K值的增大而增大，变化范围为-48.1%～87.7%，变化趋势非常明显。

3 拱梁刚度比对结构关键部位应力的影响

从以上拱梁刚度比对结构内力的影响可知，随着拱梁刚度比的变化，结构的轴力变化不明显，但是弯矩的变化较为明显，尤其是拱脚处的弯矩在恒载和活载作用下变化都比较急剧，因此需要重点研究关键部位的应力变化情况。按照运营荷载作用下最不利组合来考察跨中梁部和拱脚处的应力情况，计算结果详见表3和表4。荷载组合为主力+附加力组合，主要包括：恒载（含预应力）、ZK活载、支座沉降、摇摆力、制动力、温度力组合等。

从表3可知：当K值变化时梁体跨中截面应力变化较小，变化范围在0.5 MPa以内。这主要是因为铁路连续梁拱桥要满足先梁后拱的悬臂施工工法，梁体自身的截面刚度已经非常大，因此拱梁刚度比对跨中截面的影响较小。这种微小的变化完全可以通过增减跨中底板的钢束进行灵活调整。

从表4可知：当K值变化时拱脚最大压应力为20.1 MPa，根据《钢管混凝土拱桥设计规范》第6.2.5条以及《铁路桥涵钢筋混凝土及预应力混凝土设计规范》5.2.1条相关参数表[5]可知表4中最大压应力满足设计要求。表4中拱脚上缘最大拉应力达到5.6 MPa，拱脚处拉应力过大会引起钢管内混凝土开裂等病害。参照《铁路桥涵钢筋混凝土及预应力混凝土设计规范》第6.3.11条，对于C50钢管混凝土最大拉应力应控制在2.17 MPa以内。拱脚上缘最大拉应力从K0～4K0方向不断增加，主要是因为此时弯矩的增长效应强于惯性矩的增长效应。从K0～0.25K0方向拱脚上缘最大拉应力也不断增大，主要是因为此时惯性矩的减少效应强于弯矩的减少效应，因此拱梁刚度比的合理值应在K0附近。从表4可知K的下限值应在0.25K0～0.5K0之间;K的上限值应在K0～2K0之间。本研究考虑一定的富裕度后，以拱脚最大拉应力≤2.0 MPa作为控制目标。根据多次线性内插及有限元程序迭代试算，K的下限值为0.36K0，K的上限值为1.9K0。因此当0.36K0<K<1.9K0时，拱脚的应力指标满足规范要求。

按照K0=1/25，将K值換算为拱梁刚度比，即当换算截面面积不变时，梁拱刚度比位于1/13～1/70之间，拱脚的应力指标满足规范要求;反之超过此范围则会导致拱脚处钢管混凝土内混凝土的拉应力过大而开裂。

4 拱梁刚度比对活载挠度的影响

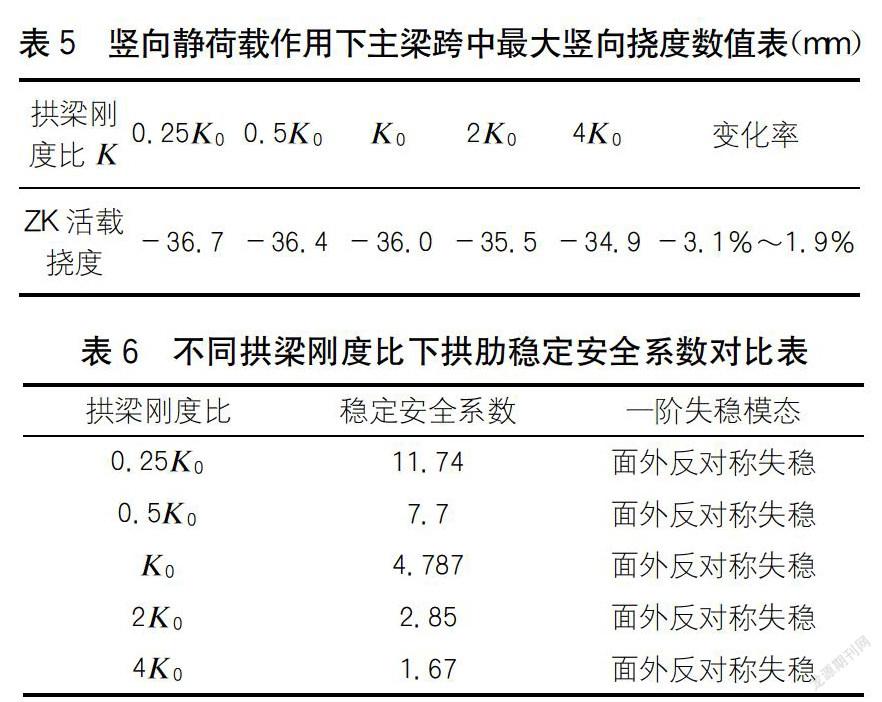
在Midas有限元程序中按照拱肋等效截面面积不变，调整拱梁刚度比，读取连续梁-拱组合结构在竖向静活载作用下梁部跨中截面的最大挠度（如表5所示）。

从表5可以看出，在各种拱梁刚度比情况下，静活载作用下最大竖向位移为36.7 mm，挠跨比为1/4 904，小于《高速铁路设计规范》[6]规定的必须<1/1 500的要求。另外当K值从0.25K0变化至4K0时，竖向静活载挠度变化范围为-3.1%～1.9%之间，因此可知拱梁刚度比在0.25K0～4K0之间变化时对主梁竖向挠度影响较小，可不作为设计的主要控制因素。

5 拱梁刚度比对拱肋稳定性的影响

对于连续梁-拱组合桥而言，主拱结构的稳定性是设计中必须重点关注的问题。按照《铁路桥涵设计基本规范》（TB10002.1-2005）[4]中，第5.2.13条规定拱肋的稳定系数宜为4～5之间。拱肋的稳定系数指拱肋的临界屈曲荷载系数，当稳定系数<4时结构的稳定性存在一定的安全隐患;>5时存在不必要的结构材料浪费。因此本文研究在拱肋等效截面面积不变的情况下，当K从0.25K0变化至4K0时拱肋的稳定安全系数。经计算研究表明：当中跨满活载（ZK活载）、边跨不加载时对连续梁-拱桥的稳定性最不利。因此采用有限元程序计算弹性屈曲稳定安全系数时荷载组合包括：自重、二期恒载、中跨满活载（ZK活载）、拱肋横向风荷载，计算结果详见表6。

表6的数据表明，连续梁-拱组合桥的一阶失稳模态都是面外反对称失稳。在拱肋的等效截面面积不变（即材料消耗基本不变）的情况下，当拱梁刚度比增加时拱的横向稳定系数逐渐减小。这主要是因为当拱肋等效截面面积不变，拱肋竖向刚度增加时，拱肋的横向结构尺寸和横向面外刚度逐渐减小，因此横向稳定系数相应逐渐减小。由于拱肋的理想设计稳定系数为4～5之间，因此从表6可知K的下限值应在0.5K0～K0之间，对应于拱肋稳定安全系数为5.0时的拱梁刚度比;K的上限值应在K0～2K0之间，对应于拱肋稳定安全系数为4.0时的拱梁刚度比。根据多次线性内插及有限元程序迭代试算，K的下限值为0.96K0，上限值为1.4K0，因此当0.96K0<K<1.4K0时拱肋的稳定安全系数处于较为理想的范围。

按照K0=1/25，将K值换算为拱梁刚度比，即当换算截面面积不变（即材料消耗基本不变），拱梁刚度比位于1/18～1/26之间时，拱肋的稳定安全系数达到设计要求的理想范围。反之当换算面积可变时，将拱梁刚度比控制在1/18～1/26之间则可以充分发挥材料的力学性能来满足拱肋稳定性，此时可以最大限度地减少截面面积，以达到节省工程投资的目的。

6 结语

在拱梁等效截面面积不变的情况下，通过对主跨（90+180+90） m连续梁-拱组合结构桥关键受力部位的内力、应力、活载挠度、稳定性进行不同拱梁刚度比的计算分析研究，可得出以下结论：

（1）拱梁刚度比在1/100～1/6.25之间变化时对恒载和活载作用下主梁跨中截面轴力、拱脚轴力影响都很小，影响范围在3%以内。

（2）拱梁刚度比在1/100～1/6.25之间变化时对恒载作用下主梁跨中截面弯矩影响最大可达32%左右，对拱脚弯矩影响最大可达79%。主要原因是随着拱的刚度增加，梁体分担自重和二期恒载产生的正弯矩逐步减小，并向拱部转移。

（3）拱梁刚度比在1/100～1/6.25之间变化时对活载作用下主梁跨中截面正弯矩的影响不大，最大不超过8%;对拱脚弯矩的影响范围最大可达88%。主要原因是随着拱梁刚度比的增加，梁体沿纵向分担活载产生的正弯矩总和逐步减小，并向拱部转移。

（4）拱梁刚度比在1/100～1/6.25之间变化时对活载作用下主梁跨中截面挠度影响不大，最大不超过4%。

（5）当拱梁刚度比在1/13～1/70之间时，拱脚的应力指标满足规范要求;反之超过此范围则会导致拱脚处钢管混凝土内混凝土拉应力过大而开裂。

（6）连续梁-拱组合结构桥的一阶失稳模态为拱肋面外反对称失稳。当拱肋换算截面面积不变（即材料消耗基本不变）时将拱梁刚度比控制在1/18～1/26能将拱肋的稳定系数控制在理想的范围。反之当换算面积可变时，将拱梁刚度比控制在1/18～1/26之间时可以充分發挥材料的力学性能来满足拱肋稳定性，此时可以最大限度地减少截面面积，以达到节省工程投资的目的。

（7）综合以上（1）～（6）条结论，考虑到本研究空跨模型的单一性存在的一些误差，并结合国内已建成通车铁路连续梁-拱组合结构桥、连续刚构-拱组合结构桥的相关参数，可将铁路连续梁-拱组合结构桥的合理拱梁刚度比确定在1/15～1/30之间。

（8）当拱肋等效截面面积一定时，将铁路大跨度连续梁-拱组合结构桥的拱梁刚度比确定在1/15～1/30之间时可以充分发挥钢管混凝土拱的材料性能，使结构的内力、应力、活载挠度、拱肋稳定性等各项指标处于较为理想的范围。反之当拱肋等效截面面积可变时，将拱梁刚度比确定在1/15～1/30之间，可以最大限度地减少拱肋等效截面面积，以达到消耗较少的拱肋材料、节省工程投资的目的。

参考文献：

[1]杨善奎，袁 明，鄢 勇，等.铁路客运专线连续梁-拱组合结构设计[J].铁道工程学报.2013（2）：48-52.

[2]GB 50923-2013，钢管混凝土拱桥技术规范[S].

[3]叶国铮，姚玲森，李秩民，等.道路与桥梁工程概论[M].北京：人民交通出版社，2006.

[4]TB 10002.1-2005，铁路桥涵设计基本规范[S].

[5]TB 10002.3-2005，铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].

[6]TB 10621-2014，高速铁路设计规范[S].