二维微流道电渗-压力驱动流流动特性解析解分析

陈春瑶 吴晋湘 赵涛 刘宏宝 祖佳红 王肖兰

摘要 用Poisson-Boltzmann（P-B）方程、外加电场的Laplace方程和描述电渗-压力驱动流流场分布的N-S方程，求解了电渗-压力驱动流流场的无量纲速度的近似解析解，以及电渗-压力驱动流与压力驱动流壁面剪切力比.定量研究不同电荷浓度、外加电场强度、zeta电势以及单位压降对流场无量纲速度分布的影响。研究表明：对于在較低雷诺数下的微细流道内流动，双电层的电粘效应确实可以引起壁面剪切应力的增大，随着沿程压降的增大，电粘效应的重要性相对减小，但仍然对流动具有较大影响，双电层电粘效应的存在是微细管道内流动特性与传统理论存在差异的原因之一。

关 键 词 微流道;电渗-压力驱动流;解析解;切应力比;速度分布

中图分类号 TN492     文献标志码 A

Analytical solution analysis of two-dimensional microchannel electroosmotic-pressure-driven flow characteristics

CHEN Chunyao， WU Jinxiang， ZHAO Tao， LIU Hongbao， ZU Jiahong，

WANG Xiaolan

（School of Energy and Environmental Engineering， Hebei University of Technology， Tianjin 300401， China）

Abstract In this paper， the Poisson-Boltzmann（PB）equation， the Laplace equation of the applied electric field， and the Naiver-Stokes equations which described the distribution of the flow field of the electroosmotic-pressure driven flow were used to solve the approximate analytical solution of the dimensionless velocity of the electroosmotic-pressure driven flow. The bed shear ratio of electroosmotic-pressure driven flow versus pressure driven flow was solved. The effects of different charge concentration， applied electric field strength， zeta potential and unit pressure drop were studied. The research shows that in the microscopic flow with lower Reynolds number， the electro-viscous effect of the double electric layer does cause the increase of the bed shear stress. With the increase of the pressure drop， the importance of the electro-viscous effect is relatively reduced， but still have a greater impact on the flow. The existence of double-layer electro-viscous effect is one of the important reasons for the differences in the flow characteristics of the micro-pipe and the traditional theory.

Key words microchannel; electroosmotic-pressure-driven flow; analytical solution; Shear stress ratio; speed distribution

0 引言

随着航空航天技术与CPU功耗的增大，器件的高散热能力成为众多科研人员的研究重点。微细通道由于几何尺寸较小，换热器的表面积与体积比较常规尺寸大得多，所以对流换热系数较高。然而随着通道尺寸的减小，微细通道中的流动出现了一些不同于常规尺度通道的现象，因此空间微尺度和时间微尺度条件下的流动问题的研究就显得十分重要。这是由于微细通道的尺寸远小于常规通道的尺寸，随着通道尺寸的减小，一些宏观流动中可以忽略的因素将可能非常重要而不可忽略。例如微流道内的动电效应、壁面粗糙度效应、表面张力效应等[1]。

Li等[2]实验研究压力驱动流电粘效应，指出对于纯水或稀释电解质溶液，电粘效应是引起流体压降增大的主要因素。Vakili等[3]运用有限差分法研究矩形微流道内幂律流体EOF流体流动以及其换热特性。Nadapana 等[4]研究微通道内压力驱动的幂律流体的电粘效应，结果发现双电层厚度及zeta电势对幂律流体电渗流的影响不同。Srinivas [5]基于非线性Poisson-Boltzmann（P-B）方程与幂律流体的动量方程求解了圆形与椭圆形微通道内电渗流速度的解析解。分析不同动电参数K、zeta电势ζ、n以及电场强度E下不同的流量比Q/Qcir。结果表明，与圆形微通道相比，椭圆形微通道的流速较低，尤其是在较低的K与ζ值.随着纵横比的增大流速降低幅度变大，对于R > 10 μm的微通道对称型电解质，物质的量浓度低至10–6 mol/L溶液仍可以获得较大K值。Lim等[6]基于电流监测法实验研究了纳米结构取向对EOF的影响，实验结果表明，垂直于微通道的纳米线使EOF速度显著降低（约20%）。 Peng 等[7]用电流斜率法系统地研究了尺寸为20 nm的单个PDMS纳米通道的电渗流速度。 Shit等[8]数值研究了滑移速度对非均匀微通道中旋转电渗流的影响，并研究不同电渗参数K和旋转雷诺数Re对非定常旋转电渗流速的影响。Rojas等 [9]数值研究了带有滑移速度的圆形微通道中牛顿流体的脉动电渗流（PEOF），并研究归一化长度、角雷诺数、电场振幅与动电参数对流速的影响。申力等[10]运用量纲分析法对微通道内非牛顿流体电渗流进行分析，结果表明微通道内幂律流体EOF速度与外加电场、zeta电势以及稠度系数均成幂律函数关系，并且稠度系数的指数为幂律指数的负数.高峰等[11]运用多物理场数值计算分析软件数值模拟了二维矩形流道的压力-电渗驱动流，通过二维流道压力分布分析了微流道中各段产生不同流型的原因。赵晓玲等[12]基于Poisson-Boltzmann方程、Naiver-Stokes方程、Nernst-Planck方程和能量方程描述微通道内双电层电势、流场、离子浓度和温度分布情况，进一步研究不同流动参数对流体传热过程的作用，讨论不同流动参数下各热效应的变化规律，分析热效应参数对流体总熵增加及各部分热效应对总熵比重的影响。

目前针对电渗流的研究主要是针对双电层存在对电渗流流型影响的研究，很少见到关于双电层电势、外加电场、溶液浓度以及压力梯度对壁面剪切力比影响的研究，另外关于压力梯度对电渗-压力驱动流速度分布的影响也少有见到。

本文基于P-B模型，结合外加电场的Laplace方程以及描述电渗流流场分布的N-S方程，求解电渗-压力驱动流的无量纲速度的近似解析解以及壁面剪切力比的解析解，并用以分析不同电荷密度、外加电场强度、zeta电势以及压降对流场无量纲速度以及壁面剪切力比的影响。

1 电渗流原理与数学基础

大多数固体与液体接觸会释放电荷，使液体形成双电层。紧靠壁面的电荷由于异种电荷间的吸附作用，牢牢地吸附在壁面不产生移动，与其极性相同的离子则会扩散到扩散层中，形成净电荷，这些带电的离子在外加电场的作用下运动，带动扩散层内的液体流动，并通过流体的粘性带动中心流体流动。

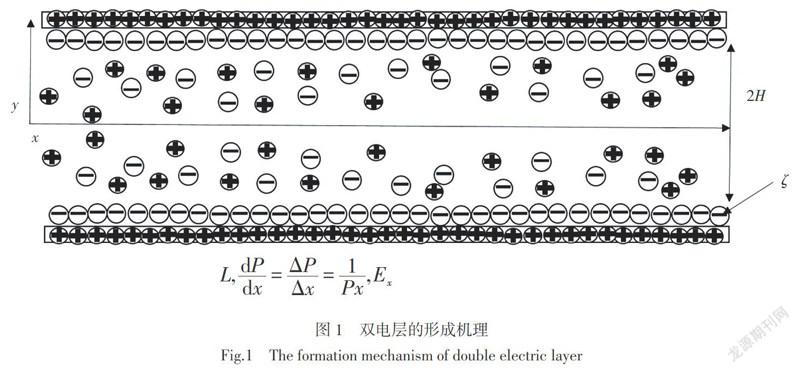
如图1，计算模型二维平板微流道的高度为2H，取H=5 μm，流道长度L>>H，上下壁面为对称壁面，zeta电势均为ζ。沿流道x方向施加外加电场Ex及单位压降dP/dx。

1.1 P-B方程

双电层的电势φ与单位体积内的净电荷密度ρe满足Poisson方程[13]：

[？2φ=-ρeεr×ε0]， （1）

式中：[εr]是电解液的相对介电常数;[ε0]代表真空介电常数。

扩散层中单位体积内净电荷密度[ρe]满足

[ρe=Σni×zi×e]， （2）

式中：[ni]表示单位体积溶液中第i种离子的数量;[zi]为离子的化合价;e是电子带有的电荷量。

微通道壁面附近扩散层离子浓度分布服从Boltzmann方程[14]分布：

[ni=n0×exp（-zieφkbT）]， （3）

式中：[kb]为玻尔兹曼常数;T为溶液温度;[n0]为溶液中主体离子数浓度，[n0=NA×CM;NA]为阿伏伽德罗常数;[CM]为离子物质的量浓度。

取溶液为对称电解液NaCl：有z+∶z-=1∶1，净电荷密度[ρe]与正负离子的浓度差线性相关：

[ρe=z×e×n+-n-   。] （4）

正负离子的浓度分布满足

[n+=n0exp （-zieφkbT）]， （5）

[n-=n0expzieφkbT]。  （6）

将式（5）、式（6）带入式（4）有

[ρe=-2zen0sinhzeφkbT]。 （7）

将式（7）带入式（1），得到描述EDL电势分布的Poisson-Boltzmann（PB）方程

[？2φ=2zen0εrε0sinhzeφkbT]。 （8）

引入无量纲参数：[Y=yH] ，[Φ=zeφkbT] .注意到[d2φdx2]=0，PB方程的无量纲形式为

[d2ΦdY2=K2sinh （Φ）]， （9）

式中：K为动电参数，K=[λ-1D×H];[λ-1D为Debye-Huckel15参数，λ-1D=（2n0e2z2εrε0kbT）12]，其倒数[λD]通常表征双电层的特征厚度。

引入线性近似[Φ≈sinh （Φ）]，并利用边界条件[Y=？1，Φ=ξ;Y=0，Φ=0且dΦdY=0]。求得

[Φ=ξcosh （KY）cosh （K）]。 （10）

1.2 Laplace方程

外加电场满足Laplace方程：

[？2Ψ=0]。 （11）

X方向电场强度[Ex]：

[Ex=？Ψ]。 （12）

利用条件 [dΨdy=0]，则 [d2Ψdx2]=0 ，且有[Ψout=0] ，[Ψin=Ψ0] ，解得：

[Ex=ΨL]。 （13）

1.3 流场的N-S方程

对流动进行如下假设：

1）流体流动为稳态流动，不随时间变化;

2）流體流动过程中忽略质量力的作用;

3）[dPdx]=常数，[dPdy]=0 ;

4）流动为完全发展的层流流动。

即流动可以简化为一维的定常流动，流动的动量方程可以简化为

[μ？？2u？y2+-dPdx+Exρe=0 。] （14）

取无量纲值：[U=uUP] ，[UP=-H22μdPdx] ，[Φ=zeφkbT]，[Y=yH]以及[Ex=ΨL]，[Px=-dxdp m/Pa]表示压强的倒数，文中提到的压降即可用此代替; [Ψ]为外加电场强度。

由式（1）知[ρe=-εrε0d2φdy2] 对[ρe]无量纲化有

[ρe=-εrε0kbTzeH2d2ΦdY2]。

对式（14）无量纲化：

[μUPH2d2UdY2-dPdx+Ex×-εrε0kbTzeH2d2ΦdY2=0]。 （15a）

化简有

[d2UdY2+2+D1d2ΦdY2=0]。 （15b）

对式（15b）进行两次积分且利用边界条件：Y = 0，[dΦdY=0]，[dUdY=0];[Y=？1] ， U = 0解得

[U=1-Y2+D（1-Φξ）]， （16）

式中，[D=2Exεrε0kbTzeH2Px×ξ]。

由式（16）可以看出影响速度分布的双电层条件主要包括溶液电荷浓度、外加电场强度、双电层zeta电势值。

1.4 切应力比

流体壁面的切应力可以表示为[16]

[τ=-μ？u？y|y=H]。 （17）

设[τ0]为压力驱动流壁面的切应力，[τ1]为电渗-压力驱动流壁面的切应力，两者比值有

[τ1τ0=-μ×upH×？U？Y|Y=1-μ？up？y|y=H] 。  （18）

对式（18）化简得到

[τ1τ0=-12？U？Y|Y=1=122+K×D×sinh （K）cosh （K）] 。 （19）

2 计算结果

2.1 溶液浓度对无量纲速度的影响

计算用流道材料为硅基板，溶液为NaCl，在一定的范围内ζ电势与离子浓度的关系为[14]

[ζ（c）=a0+a1ρc]  ， （20）

式中[：a0]、[a1] 为温度、pH值、基板材料、离子种类等的函数。对于NaCl溶液pH=7时，Revil[17]实验测得[a0=0，a1≈-20 mV ]，[ρc=-lgCi]  因而式（20）有

[ζ（c）=20lg（CM）]，                           （21）

式中，CM为溶液物质的量浓度，mol/L 。

计算模型取x方向电场强度[Ex=105]V/m，[Px=-2×10-5]m/Pa，分别取溶液物质的量浓度为10-3，10-4，10-5，10-6 mol/L，其他常数均取自表1，带入式（16）、式（19），计算结果如图2。

由图2a）可见，在计算用溶液物质的量浓度范围内（10-3～10-6 mol/L），随着物质的量浓度的减小，双电层厚度增大，双电层电势的绝对值随之增大，无量纲速度增大。由图2b）可见随着物质的量浓度的减小，壁面剪切力比随之减小。即随着溶液物质的量浓度的减小，无量纲速度增大，壁面剪切力反而减小，这可能是由于随着物质的量浓度的减小，双电层厚度增大，同时增大了双电层电粘效应的影响范围。

2.2 电场强度对无量纲速度的影响

计算模型取溶液物质的量浓度C = 10-4 mol/L，由式（21）计算得ζ = -80 mV，Px = -2[×]10-5 m/Pa，分别取x方向电场强度Ex分别为2.5[×]104，5[×]104，1[×]105，2.5[×]105 V/m，其他數据由表1提供，带入式（16）、式（19）计算结果如图3所示。

由图3可见，随着电场强度的增大，无量纲速度与壁面剪切应力随之增大，双电层厚度并未发生改变。这是由于随着电场强度的增大，溶液间双电层的电粘效应增强，而电粘效应的作用距离并未改变，因而导致壁面剪切力增大。

2.3 zeta电势对无量纲速度的影响

由于ζ电势与温度、pH值、基板材料、离子种类等溶液性质相关，计算模型取ζ电势分别为-20，-40，-60 mV[17]，上述电势值均在文献图表中体现，不妨大胆的假设介于-20 mV到-60 mV之间双电层电势均可取到。溶液物质的量浓度C=10–4 mol/L，Px= -2[×]10–5 m/Pa，x方向电场强度Ex = 105 V/m，其它数据由表1提供，带入式（16）、式（19）计算结果如图4。

由图4可见随着ζ电势绝对值的增大，无量纲速度与壁面剪切应力也随之增大。双电层厚度并未随之变化，与ζ电势无关。

2.4 压降对壁面剪切力比的变化

这里指的压降为单位长度压强的变化，为计算方便取其倒数即Px，计算模型取溶液物质的量浓度C=10–4 mol/L，由式（21）计算得ζ = -80 mV，x方向电场强度Ex = 105 V/m，分别取Px = -2[×]10–5 m/Pa、Px = -2[×]10–6 m/Pa、Px = -2[×]10–7 m/Pa、Px = -2[×]10–8 m/Pa其他数据由表1提供，带入式（19）计算结果如表2。

由表2可见，随着x方向单位长度压降的增大，即随着压力驱动速度的增大，壁面剪切力比随之减小，这表明电粘效应的重要性相对减小。将Px = -2[×]10–8 m/Pa代入[UP=-H22μdPdx] （即压力驱动流中心速度）可以求得[UP=]0.694 4 m/s，由表2可以看到在本文的通道尺寸条件下即使在压力驱动流达到0.694 4 m/s双电层的电粘效应对流动仍具有很强的影响。

3 结论

基于P-B模型，结合外加电场的Laplace方程以及描述电渗流流场分布的N-S方程，求解电渗-压力驱动流的无量纲速度的近似解析解，并分析不同电荷密度、外加电场强度、zeta电势以及压降对流场无量纲速度的影响，得出以下结论：

1）随着溶液物质的量浓度的减小，ζ电势绝对值增大，无量纲速度增大，摩擦力反而减小。这有可能是由于随着溶液物质的量浓度的减小，双电层厚度随之增大，双电层的电粘效应对壁面剪切力的影响降低。

2）外加电场强度与ζ电势具有相似的作用，都能同时增大无量纲速度与壁面剪切力。这是由于随着电场强度或ζ电势的增大，溶液间双电层的电粘效应增强，而电粘效应的作用距离并未改变，因而导致壁面剪切力增大。

3）在较低雷诺数下的微细流道内流动，双电层的电粘效应确实可以引起壁面剪切应力的增大，随着沿程压降的增大，电粘效应的重要性相对减小，但仍然对流动具有较大影响，双电层电粘效应的存在是微细管道内流动特性与传统理论存在差异的原因之一。

参考文献：

[1]    KOO J，KLEINSTREUER C. Analysis of surface roughness effects on heat transfer in micro-conduits[J]. International Journal of Heat and Mass Transfer，2005，48（13）：2625-2634.

[2]    LI D Q. Electro-viscous effects on pressure-driven liquid flow in microchannels[J]. Colloids and Surfaces A：Physicochemical and Engineering Aspects，2001，195（1/2/3）：35-57.

[3]    VAKILI M A，SAIDI M H，SADEGHI A. Thermal transport characteristics pertinent to electrokinetic flow of power-law fluids in rectangular microchannels[J]. International Journal of Thermal Sciences，2014，79：76-89.

[4]    NADAPANA V，SIRSHENDU D. Electroviscous effects in purely pressure driven flow and stationary plane analysis in electroosmotic flow of power-law fluids in a slit microchannel[J]. International Journal of Engineering Science，2010，48（11）：1641-1658.

[5]    SRINIVAS B. Electroosmotic flow of a power law fluid in an elliptic microchannel[J]. Colloids and Surfaces A：Physicochemical and Engineering Aspects，2016，492：144-151.

[6]    LIM A E，LIM C Y，LAM Y C，et al. Effect of nanostructures orientation on electroosmotic flow in a microfluidic channel[J]. Nanotechnology，2017，28（25）：255303.

[7]    PENG R，LI D. Electroosmotic flow in single PDMS nano-channels [J]. Nanoscale，2016，8（24）：12237-12246.

[8]    SHIT G C，MONDAL A，SINHA A，et al. Effects of slip velocity on rotating electro-osmotic flow in a slowly varying micro-channel[J]. Colloids and Surfaces A：Physicochemical and Engineering Aspects，2016，489：249-255.

[9]    ROJAS G，ARCOS J，PERALTA M，et al. Pulsatile electroosmotic flow in a microcapillary with the slip boundary condition[J]. Colloids and Surfaces A：Physicochemical and Engineering Aspects，2017，513：57-65.

[10]  申力，李鳴，杨大勇. 微通道内幂律流体电渗流的量纲分析[J]. 南昌大学学报（工科版），2015，37（4）：377-381.

[11]  高峰，石则满，冯鑫，等. 微流控芯片中电渗流的数值模拟与仿真研究[J]. 传感器与微系统，2017，36（11）：53-55，59.

[12]  赵晓玲，杨大勇，王阳. 电渗流中传热传质过程与熵的分析[J]. 应用数学和力学，2017，38（3）：310-320.

[13]  REN L Q，ESCOBEDO C，LI D Q. Electroosmotic flow in a microcapillary with one solution displacing another solution[J]. Journal of colloid and Interface Science，2001，242（1）：264-271.

[14]  KIRBY B J，HASSELBRINK E F. Zeta potential of microfluidic substrates：1. Theory，experimental techniques，and effects on separations [J]. Electrophoresis，2004，25（2）：187-202.

[15]  KARNIADAKIS G E，BESKOK A，Aluru N. Microflows and Nanoflows：fundamentals and simulation [M]. New York：Springer Science Business Media，Inc，2005.

[16]  赵孝保 ，周欣. 工程流体力学[M]. 南京：东南大学出版社，2010.

[17]  REVIL A ，PEZARD P A，GLOVER P W J. Streaming potential in porous media：1. Theory of the zeta potential [J].  Journal of Geophysical Research：Solid Earth，1999，104（B9）：20021-20031.

[责任編辑    田    丰]