拱桥短吊杆索力精确测量研究

倪应谦 陈齐风

摘要：文章以某钢管拱桥为项目依托，针对钢管拱桥短吊杆索力测试不精确的情况，引入采用迦辽金方法的索体附带质量块的频率法索力精确计算公式，并将该精确计算方法与吊杆索力设计方法对比，验证了该计算方法的有效性。

关键词：短吊杆;频率法;附加质量;迦辽金方法

中图分类号：U443.38 文献标识码：A DOI：10.13282/j.cnki.wccst.2019.09.028文章编号：1673-4874（2019）09-0096-04

0 引言

近年来，吊杆拱桥以其跨越能力强，结构自重轻，形式美观，造价低廉的优点在我国大量建造。由于吊杆缆索的防护技术较弱，许多吊杆的护套在使用10余年即发生老化，从而影响钢管拱桥的正常使用乃至结构的安全，从而不得不重新更换吊杆。在吊杆更换过程中，需要密切注意吊杆的索力变化情况.对于长吊杆，频率法索力测试精度可满足工程要求。然而，位于桥梁拱脚附近的吊杆，通常长度很短（长度为吊杆直径200倍以内），此时吊杆的锚固条件、护筒、减震器、吊杆刚度等因素会对吊杆频率产生较大影响，而这种影响的大小往往很难确定.此时采用常规的频率法测试得到的吊杆索力误差很大，存在误判的可能性较大，甚至会得出错误的结果。如何对短吊杆索力进行精确测试，一直是未解决的工程难题。因此，在对吊杆拱桥这类桥型进行检测或施工监测中，急需一种能够精确测定短吊杆索力的方法。目前，在工程上常用的索力的测试方法主要包括磁通量法、压力表法、压力传感器法和频率法.其中，频率法是使用最广泛的方法，因为其操作简单，测试精度高。

本文主要结合某吊杆拱桥的吊杆达到使用寿命后更换新吊杆张拉过程中实测结果和千斤顶张拉力的误差等数据，在有限元建模分析和比较后，将吊杆等效为具有等效计算长度的简支张拉索，在吊杆中间附加质量块，引入建立了吊杆中部附加质量块前后拉索的振动平衡方程，优化形成利用附加质量前后吊杆测试振动频率识别吊杆等效计算长度LO的算法，进行质量块对索力的敏感性分析。对比分析质量块对频率法测索力的影响，验证引入索体附带质量块的频率法索力精确计算公式的有效性。

1频率法测试理论

1.1频率法测试原理

频率法是利用力和频率之间的关系，同时针对特殊的约束条件（铰接或固接），求解出相应的方程式。

当拱桥吊杆两端被视为固接时，可视为张紧弦模型。根据结构动力学知识，弦在平面内做横向振动，如图、所示。此时，振动方程可以列出，并可通过数学方法获得方程的解：

其中l是吊杆计算长度;f是索（弦）振动基频。由于振动会产生n阶频率f=nf，若基频测试效果不理想，则使用差值法可以间接求取。

当拱桥吊杆两端被视为铰接时，忽略自重影响的情况下，则振动方程为：

1.2 附带质量块的频率法短吊杆索力精确计算公式

引入采用迦辽金方法推导的短吊杆索力精确计算方法，推导过程如下：

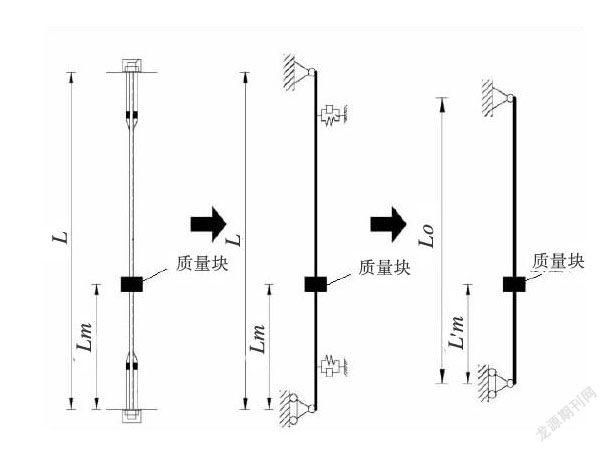
将吊杆的边界条件简化为在简支吊杆的相应横向位置处附加上了一个阻尼和弹簧支承。此时，可将横向位置处附加阻尼和弹簧支承视为对吊杆支承的加强，相当于减小了吊杆的计算长度。因此，在振动分析时，可将吊杆简化为具有等效计算长度L的简支张拉索，如图2所示.考虑拉索弯曲刚度EI的影响，由力的平衡方程及弯矩平衡方程可得出拉索的振动平衡方程：

式中，吊杆刚度EI、吊杆材料密度ρ和吊杆截面积A是已知的，吊杆振动频率W可由振动仪器测试得出。因此，只需要确定吊杆的有效计算长度L，便可由实测振动频率w分析得出吊杆索力为T。为了确定吊杆的有效计算长度L，在距吊杆底端L处附加一个质量为M的质量块，见下页图3。

1.3 现场测试

通过收集现场数据及对相关数据进行处理之后，可得到实测频率，通过频率和索力的对应关系，并通过式（10）的换算，即可求出吊杆索力值。测量工作步骤见图4。

2 工程案例

某吊杆拱桥为广昆高速（石埠北立交至坛洛段）G80线上的一座大跨径桥梁，见图5。该桥结构形式为中承式钢管混凝土桁架拱桥，全桥长349m，跨径组合为4×20m+190m+3x20m，主桥结构为钢管混凝土桁架拱，采用单孔净跨径190m的中承式钢管混凝土桁架拱桥，净跨比为1/4.5，主拱轴线为无铰悬链线，拱轴系数m=1.167。拱肋为等截面钢管混凝土桁架结构.拱肋断面采用φ820×12mm和φ820×14mm钢管组成拱肋上、下弦杆，截面高4.3m、宽2.0m。主桥两侧27组吊杆共54根，吊杆间距为5.1m。南宁岸引桥为4×20m的先张法预应力混凝工连续空心板;坛洛岸引桥为3×2m的先张法预应力混凝土连续空心板。目前该桥已投入运营超过13年，出现了吊杆护套破损、锚头积水、空心板开裂等病害。2016年5月，决定对该桥进行全封闭交通维修施工，主要进行该桥吊杆的更换，旧吊杆为85φ7mm的平行钢丝索，新吊杆为25φ15.2mm、27φ15.2mm的成品钢绞线索。

其中本桥的短吊杆有3条，分别为1#/27#、2#/26#、3#/25#吊杆，其计算长度分别为：0.95m、3.07m、5.78m，此处的计算长度为下拱肋底部到桥面的距离。此处以3#吊杆索力测试为工程案例，并建立索体有限元分析模型，对比理論计算结果与有限元计算结果。3#/25#新吊杆的线密度为38.07kQ/m，其计算索长仅为5.78m，测试频率为14.22Hz，采用的质量块重量为22.5kg，吊杆参数如表1所示;吊杆附加质量块如图6所示。

3计算结果分析

通过对25#吊杆测试频率采用经典方法与本文提出的精确计算方法及与吊杆索力设计值对比，得到结果如表2所示。

4 结语

本文以实体工程中某吊杆拱桥为项目依托，对短吊杆索力测试不精确的情况进行针对性的分析.通过对比计算方法计算测试索力后得到以下结论：

（1）通过对两种计算方法的对比，可知本文提出的方法更接近于设计索力，误差为7%;

（2）当质量块处于吊杆中间时，对频率影响效应最大;

（3）对于越长的吊杆，附加质量的位置和大小影响越明显。

（4）在锚固端附近吊杆质量密度的改变对索力敏感性较小。