重视过程 在“再创造”中建构新知

程红霞

【摘要】《义务教育数学课程标准（2011年版）》关于教学建议有这样的一句话：“重视过程，要处理好过程与结果的关系。”这句话向我们传递了至少三层意思，一是我们要改变以往只重知识技能目标的观念，深刻认识到过程性目标的重要性;二是重视过程不是忽略结果，过程与结果之间的辩证关系是我们首先要明确理解的;三是这句话为教学实施过程指明了大方向，但具体如何操作尚不明确。作为一线教师，我们需要更深入地思考“在操作层面上，如何才是重视过程，如何才能处理好过程与结果的关系”。

【关键词】再创造;小学数学;有余数除法中余数与除数的关系

首先，我们应理解什么是“过程”，什么是“结果”。过程既是学生学的过程，又是教师教的过程，结果是指学生理解了数学知识的本质，并能运用知识解决问题。为什么要重视过程？学生在数学学习活动中收获到的绝不只是我们看到的知识理解、技能方法掌握，这只是冰山一角，而如数学素养的整体提升、个人品质的形成、学习兴趣的发展等，才是让学生终身受益的宝贵财富。

如何在具体实践中进行操作呢？数学教育家弗赖登塔尔说：“学生学习数学唯一也是最佳的方法就是‘再创造’，由学生本人把要学习的东西自己发现或创造出来，教师的任务是引导和帮助学生进行这种再创造工作，而不是把现成的知识灌输给学生。”下面笔者以二年级下册《有余数除法中余数与除数的关系》这一内容为例，详细解读如何让学生“再创造”，及如何在“再创造”中建构新知。

一、文本阅读

备课之前的文本阅读、教材解读非常重要，而对不同版本的教材进行比较阅读是解读教材的重要方式。对于《有余数除法中余数与除数的关系》这一内容，不同的教材是怎样呈现的呢？彼此的优劣如何？能体现“再创造”的理念吗？

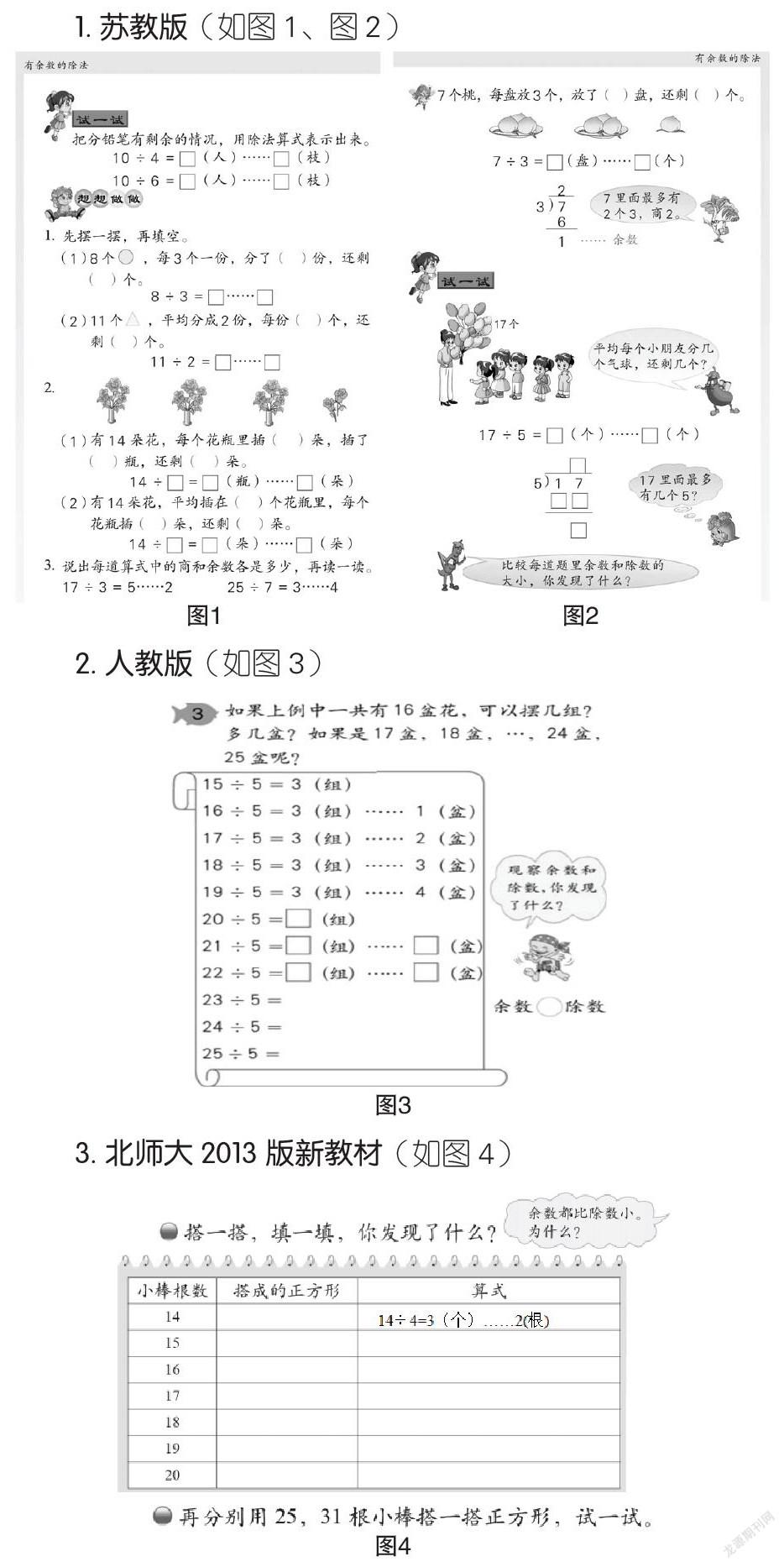
1. 苏教版（如图1、图2）

2. 人教版（如图3）

3. 北师大2013版新教材（如图4）

从以述文本中可以看出，苏教版教材通过创设分气球的情境，在解决问题中引发学生对余数与除数关系的讨论;人教版教材与北师大版新教材都是设计了一个较大的探究活动，以不完全归纳法的形式呈现一组有规律的除法算式，从而引导学生探究发现余数与除数的关系，但是两者呈现方式存在区别，前者以文字创设情境，再以算式表征，而后者不仅有算式表征，还有图形表征，更直观形象，学生更容易发现规律、建构新知。三种教材的比较，让我们清晰地看到课程改革理念的贯彻和编者思路的改进。

学生在学习这一内容时最大的难点是太抽象，难以建构新知，苏教版教材以若干小情境的堆砌来引导学生理解余数与除数的关系，情境碎片化、独立化不利于学生观察规律，学生难以真正理解余数与除数的关系。人教版与北师大新版教材都体现了“再创造”的思想，在一个大的探究活动中，“由学生本人把要学习的东西自己发现出来”。北师大版新教材更是用了两种表征方式，在表格中清晰地呈现被除数、余数的规律变化，真正突破了这一知识内容的难点。

二、教学实施

笔者赞同北师大2013新版教材的处理方式。教材中展现了学生的“动态”学习过程，用14、15、16……20一组连续根数的小棒搭正方形，在操作过程中列出相应的除法算式，引导学生探索余数与除数的关系。在搭小棒和列式的过程中，学生会很快发现余数的变化规律，小棒有时正好用完，而有时会剩余，剩余的小棒数量逐1增加，但增加到一定程度时会“中断”，这时小棒刚好用完。学生再继续下去，会发现这又是一个“循环”。

在实际教学中，对于这一设计，笔者基本上未做任何改动，因为这已经是非常好的“再创造”过程。在让学生利用教材中的表格进行自主探索后，笔者引导学生观察表格，发现规律。学生很善于观察与表达，说出了“图与算式是一样的意思”“商就是表示擺了几个正方形，余数就是剩了几根小棒”“余数都是1、2、3”。学生不能表达出“余数比除数小”，这时教师可以追问：“余数为什么只能是1、2、3，不能是4、5、6和其他一些更大的数吗？”这个问题提出后，学生反应很热烈，纷纷举手发表自己的意见，他们能够清楚地说明为什么余数只能是1、2、3，而不能是4或大于4的数。个别学生甚至能进一步思考到“这是摆正方形，所以余数不能超过4;如果是摆五边形，那么余数可以是4，但不能超过5。”这正是透彻理解余数与除数关系的表现。至此，学生将自然而然地发现“余数要比除数小”这一概念。

三、策略梳理

（1）重视过程，就是要从学生的角度设计课堂教学，让学生经历“再创造”的过程，自己去“发现或创造”出知识。我们要尊重学生的知识经验基础，按照科学的认知规律设计学生的学习活动，设计教师的组织、引导方式。

（2）要给予学生充足的时间、空间来经历、体验、探索，学生经历了丰富的数学学习活动过程，有了经验和思考，才能水到渠成地形成结果。

（3）“再创造”后的交流讨论非常重要，这是学生的认知由量变到质变的关键过程。在这里教师要放慢脚步、浓墨渲染，抓住认知冲突，设计问题引领，引导学生在质疑、完善、提升的过程中真正领悟数学知识的本质，获得预期的结果。

【参考文献】

庄惠梅.小学数学“再创造课堂”初探[J].学周刊，2019（17）：90.