巧用图形变换培养空间思维能力

黄秀科 徐花

摘要：本文通过初中七年级三种应用题类型的解题方法，探索方程建模的培养方法与途径，旨在多种多样的课堂教学方法中，归纳出适合学生学习实际和效果明显的教学技巧，给广大教学一线的初中数学教师提供学习和借鉴.

关键词：初中;数学;教學

吃透教材，探究新课程理念，加大课改力度，创设新型的教学模式，提升数学空间想象能力。

一、背景

2017年春季学期开始，学校委托我在3年内培养新入职的年轻教师徐花，快速成长为教学能手，2018年11月，我们师徒二人受邀参加右江区在片区龙头学校百色市五中举行的《青年教师汇报课》上亮相一节公开课。我两设计了一节“借助平移、翻折、旋转的图形变换理解三角形全等”的探究课。课前准备充分，展示课上师生互动活跃，学生的发散思维表现得淋漓尽致，得到了现场专家和教师的认可。现将本节课的设计和领悟整理成文，以便和同行们参考交流。

全等三角形的教学是八年级上册内容，是初中生进入几何推理的入门，是几何教学中图形辨认的启蒙。

二、目标

本节课是在学生学完全等三角形“SAS、ASA、AAS、SSS”四个判定的基础上加以提升的综合课，其目的是培养“空间思维”这一数学核心素养的能力，让教学从感性认知提升到理性认识，挖掘、突破教学难点。

三、教学设计环节

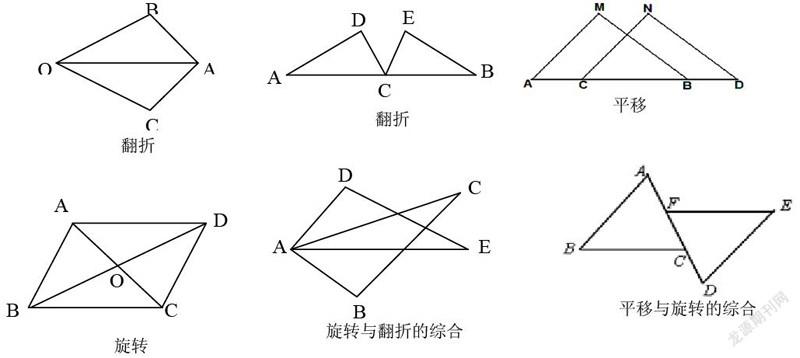
1.用平移、翻折、旋转的图形变换直观识别常见的全等三角形图形，打开空间想象引入课堂。

课堂展示方式：课堂中让学生合作讨论、口头描述变换方式，教师利用几何画板演示，在实践课中让学生动手操作体验几何画板加深理解，从感性认知中打开“空间想象思维”的数学核心素养。

2.以条件探索的形式匡实基础，培养空间想象力。实例展示

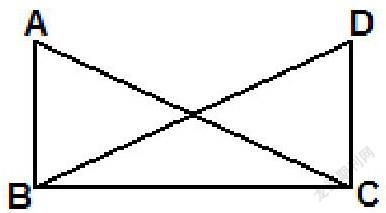
例1 如图，

（1）猜猜图中可能有几对三角

形全等;

（2）在△ABC和△DCB中，

AC=DB，还需增加一个

条件，可使△ABC ≌ △DCB（不再增加任何字母与辅助线）。

（3）用平移、翻折或旋转的图形变换描述把△ABC与 △DCB叠合的过程。

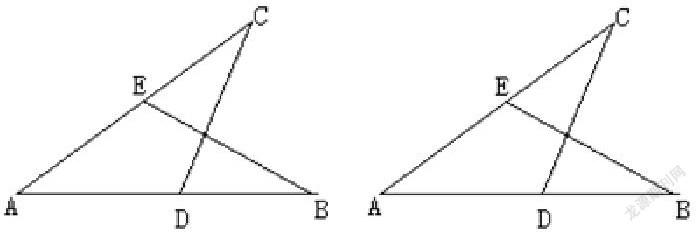
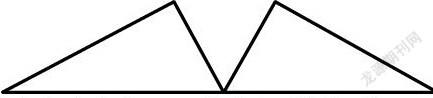
例2 如图

猜猜图中可能有几对三角形全等;

（1）能用字母表示可能全等的三角形有几对？（用平移、翻折或旋转的图形变换想象并加以描述）

（3）已知在△ABE和△ACD中，AB = AC，要使△ABE ≌ △ACD，还需添加一个条件，这个条件可以是 。

反思：该例题设计的用意

（1）突出几何学习的常用方法→猜测结论，再加以论证;

（2）利用图形变换培养识图能力;

（3）在教材传统教法上推出新的理念，利用多种手段从不同角度解决问题;

（4）背景设计打破常规、新颖，增加课的趣味性。

3.以尝试加实践的课堂模式，寻找证明思路，培养三角形全等证明的数学建模核心素养。示例展示

试一试

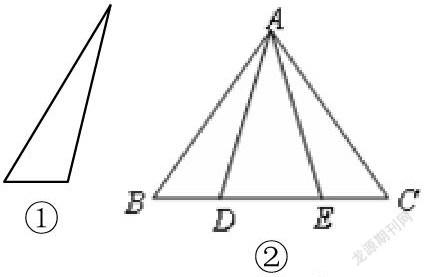
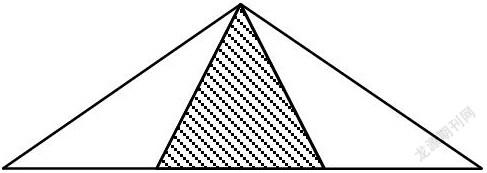
例：（1）利用平移、翻折或旋转的知识把两个图①拼接成图②（观察图②中两个图①所在的位置）

（2）结合图②编写一道与

三角形全等有关的证明题。

仿上例：（1）例用平移、翻折或旋转的知识把两个图③拼接成图②（描述拼图过程）

（2）结合图②再编写一道与三角形全等有关的证明题

效果：（1）打开了学生的“发散思维”这一数学核心素养;

（2）共享资源丰富多彩;

（3）跃跃欲试、合作分享养成习惯;

（4）合作、分享等德育教育融入课堂;

（5）例题难易梯度科学合理（由直观拼图层层深入转向逻辑推理）。

4.以动手实验操作题型收尾课堂，体现对知识的认知由感知动手实践提升到理论成果的数学核心素养。

示例 体验、合作完成题

将两块（含60°角）相同的三角板如图摆放，两斜边在同一直线上，60°角的顶点拼接在同一点上。

①：探究两直

角顶点与60°角顶

点所围成三角形的形状（在图中标上字母后说明理由）;

②：将①中右边三角板沿斜边向左平移到直角顶点重合后停止，画出平移停止后的图形。判断重合部分三角形的形状（说明理由）;

③继续探究 重合部分三角形面积与其中一块三角板面积的数量关系（说明理由）

②、③的图 →

要求学生动手画图

反思：此题设计由浅入深，知识迁移自然。第一问让学生找到解题的方向为第二问埋下伏笔;第二问难度是审清题意后准确的画出相应图形，只要图形出现，解法思路自然柳暗花明;第三问继续探究转入面积，体现了“知识多元化”的数学核心素养。