T-S模糊模型的FGD系统pH值建模研究

【摘 要】目前，湿法石灰石-石膏烟气脱硫系统（即FGD系统）在火电厂脱硫系统中占绝大比例。FGD系统采用化学方法除掉烟气中的二氧化硫的方式，其中pH值是一个重要的参数，关系到化学反应的指示值。对此，应用T-S模糊神经网络模型以吸收塔pH值为对象进行数学建模，并且针对广东省能源集团有限公司珠海发电厂装机容量700WM的1#机组脱硫吸收塔pH值实时数据信号进行仿真处理。通过对该模型参数的预测学习以及与实际输出的对比，得到符合条件的仿真模型。模型预测结果能够反映机组真实情况，有进一步研究的价值。

【Abstract】At present， wet limestone-gypsum flue gas desulfurization system （FGD system） accounts for most of the desulfurization systems in thermal power plants. FGD system uses chemical method to remove sulfur dioxide from flue gas. Among them， pH is an important parameter， which is related to the indicator value of chemical reaction. In this regard， T-S fuzzy neural network model is applied to carry out mathematical modeling with the pH value of absorption tower as the object， and the real-time data signal of pH value of desulfurization absorption tower of unit 1 with the installed capacity of 700WM in Zhuhai Power Station of Guangdong Energy Group Company Limited. is simulated. Through the prediction learning of the model parameters and the comparison with the actual output， the simulation model conforming to the conditions is obtained. The model prediction results can reflect the real situation of the unit， which has the value of further research.

【關键词】吸收塔;pH值;T-S模糊模型;神经网络;仿真

【Keywords】absorption tower; pH value; T-S fuzzy model; neural network; simulation

【中图分类号】N945.12                                          【文献标志码】A                                【文章编号】1673-1069（2019）06-0184-02

1 引言

在日常生活中，有很多的时变系统，并且需要研究的对象比想象中复杂很多。现场实际因素的影响使得并不容易将应用理论和实验应用在研究对象上，对此，最常用的方法就是建模。在数学领域建模并不能够达到具体化，转换为借助于一个系统以及处于过程中的相关变量之间的某种关系来反映实现的数学结构[1-2]。脱硫系统能够正常运行，其中pH是最重要的控制参数之一，直接关系到脱硫效率和脱硫效果。针对珠海发电厂FGD系统的运行情况，其值在5.5～6.0是最佳范围，整个控制目的在于保证pH稳定[3-4]。基于控制FGD系统pH值的非线性、多时变、强耦合的特点，用T-S模糊模型对特定值进行数学建模来进行分析及优化[5]。

2 模型概况

面对多维模糊推理中的推理规则庞大的问题，由Takagi和Sugeno提出了一种新的模糊推理模型，称为Takagi-Sugeno（T-S）模糊模型。模型的输入函数是规则后件：

Ri：ifxisAithenyi=fi（x）i=1，2，…，n（1）

这种语言规则描述的模型展开第i条规则可写为：

Ri：ifx1isA1andifx2isA2and…andifxrisAirthenyi=P i0+P i1x1+P i2x2+…+P irxr （2）

这里，Air在模糊系统中是第i条规则前件的模糊集合;Pim（m=1，2，……，k）是系统参数;x=[x1，x2，……，xr]是输入变量;yi是输出变量，输入模糊，输出确定，整个模糊推理过程的输入与输出的关系呈线性。

对输入变量x来说，应用模糊规则来计算每个输入变量的隶属度：

μ=exp（-（xm-c）2/b），m同上;i同上（3）

这里，c、b是隶属度函数的中心和宽度。把隶属度进行计算，应用连乘算子：

ωi=μ（x1）*μ（x2）*…*μ（xk）i同上     （4）

通过计算得到输出值yi。

yi=ωi（P+Px1+Px2+…+Pxk）/ωi （5）

式中，k是输入参数;n是子集数。

3 网络辨识

由图1可以看出，T-S模糊神经网络是由五层从左向右的网络组成：前为输入层，中间区域为输出层、模糊化层和模糊条件层，后端为输出层;与输入层连接的是输入向量x;模糊隶属度值μ是模糊化层将隶属度函数公式（3）对输入值进行模糊化得到的。模糊连乘公式（4）用于模糊条件层，而输出则是通过模糊决策层采用公式（5）计算得出。

学习算法如下：

①误差的计算

e=（yd-yc） （6）

这里，yd是期望輸出;yc是实际输出;e是期望输出和实际输出的误差。

②系数的修正

P（k）=P（k-1）-α（7）

=（yd-yc）ωi/ωi *xm （8）

这里，P是神经网络系数;α是学习效率;xm是输入参数;ωi是输入参数隶属度连乘积。

③参数的修正

c（k）=c（k-1）-β （9）

b（k）=b（k-1）-β（10）

式中，c、b分别为隶属度函数的中心和宽度。

4 建模与仿真

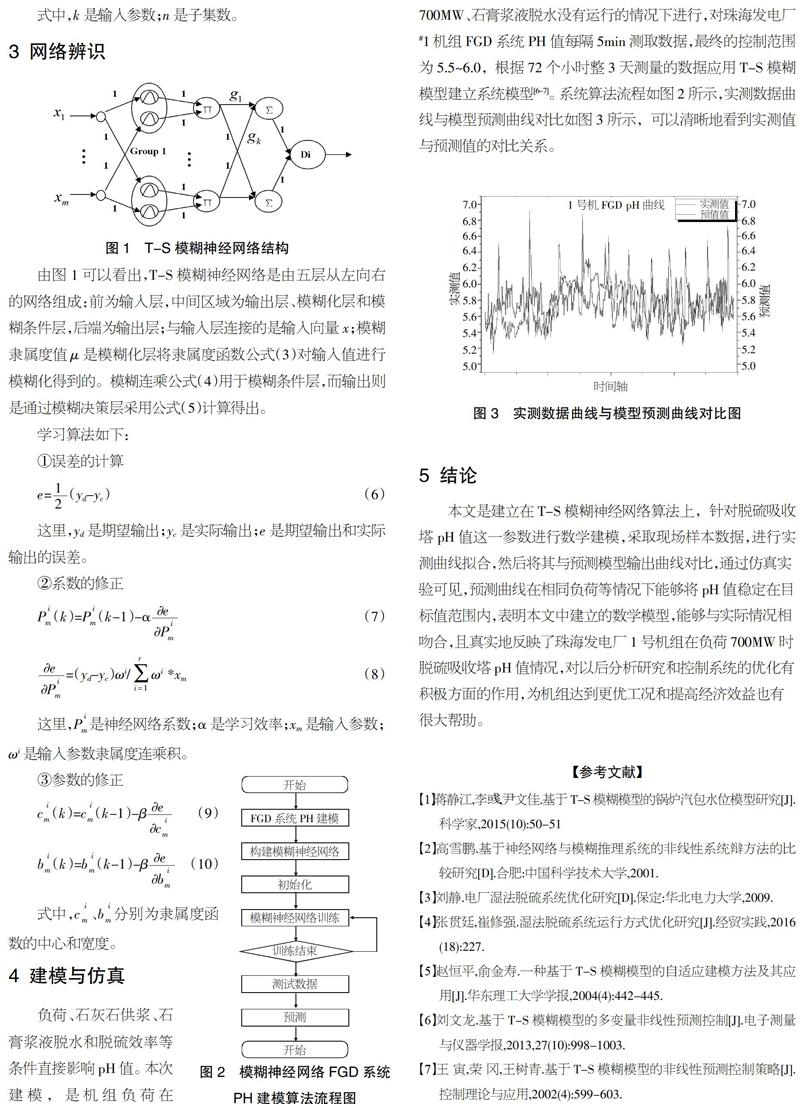
负荷、石灰石供浆、石膏浆液脱水和脱硫效率等条件直接影响pH值。本次建模，是机组负荷在700MW、石膏浆液脱水没有运行的情况下进行，对珠海发电厂#1机组FGD系统PH值每隔5min测取数据，最终的控制范围为5.5～6.0，根据72个小时整3天测量的数据应用T-S模糊模型建立系统模型[6-7]。系统算法流程如图2所示，实测数据曲线与模型预测曲线对比如图3所示，可以清晰地看到实测值与预测值的对比关系。

5 结论

本文是建立在T-S模糊神经网络算法上，针对脱硫吸收塔pH值这一参数进行数学建模，采取现场样本数据，进行实测曲线拟合，然后将其与预测模型输出曲线对比，通过仿真实验可见，预测曲线在相同负荷等情况下能够将pH值稳定在目标值范围内，表明本文中建立的数学模型，能够与实际情况相吻合，且真实地反映了珠海发电厂1号机组在负荷700MW时脱硫吸收塔pH值情况，对以后分析研究和控制系统的优化有积极方面的作用，为机组达到更优工况和提高经济效益也有很大帮助。

【参考文献】

【1】蒋静江，李彧，尹文佳.基于T-S模糊模型的锅炉汽包水位模型研究[J].科学家，2015（10）：50-51

【2】高雪鹏.基于神经网络与模糊推理系统的非线性系统辩方法的比较研究[D].合肥：中国科学技术大学，2001.

【3】刘静.电厂湿法脱硫系统优化研究[D].保定：华北电力大学，2009.

【4】张贯廷，崔修强.湿法脱硫系统运行方式优化研究[J].经贸实践，2016（18）：227.

【5】赵恒平，俞金寿.一种基于T-S模糊模型的自适应建模方法及其应用[J].华东理工大学学报，2004（4）：442-445.

【6】刘文龙.基于T-S模糊模型的多变量非线性预测控制[J].电子测量与仪器学报，2013，27（10）：998-1003.

【7】王 寅，荣 冈，王树青.基于T-S模糊模型的非线性预测控制策略[J].控制理论与应用，2002（4）：599-603.