铁路轨道信号检测仿真及硬件系统设计

金鑫

【摘 要】为快速准确地测试ZPW2000移频轨道电路信号参数，论文基于STM32单片机，通过欠采样方式以及快速傅里叶变换（FFT）解调算法，设计ZPW2000移频轨道电路信号载波频率和低频调制频率等的检测方案。

【Abstract】In order to quickly and accurately test the signal parameters of ZPW2000 frequency shifting track circuit， based on the STM32 single-chip microcomputer and by means of the under-sampling and fast Fourier transform （FFT） demodulation algorithm， the detection scheme of ZPW2000 frequency shifting track circuit signal carrier frequency and low-frequency modulation frequency is designed.

【关键词】移频信号;STM32;欠采样;FFT

【Keywords】frequency-shift signal; STM32; under-sampling; FFT

【中图分类号】U284.91                                           【文献标志码】B                                【文章编号】1673-1069（2019）06-0144-03

1 引言

ZPW2000移频轨道电路是我国目前应用最为广泛的信号制式，具有抗干扰性强，频带较窄，性能稳定等优点。该调制信号是把低频信号搬移到高频信号上，从而形成一个幅度不变，频率随低频信号不断变换的移频键控信号。

移频信号的检测主要分为时域法和频域法。时域法抗干扰能力差，信号特性检测不直观。时域法抗干扰能力强，需要通过大量的采样点计算得到移频信号的分析数据，所以频域分析的实时性低，但所得的频域图能直观地反映出信号状态。因此，本文采用频域分析法，通过欠采样，快速傅里叶变换[1]（FFT），实现对ZPW2000移频信号的实时准确检测。

2 移频信号

ZPW2000的中心频率有四个，分别为：1700Hz、2000Hz、2300Hz、2600Hz。频偏为±11Hz。低频调制信号在10.3Hz到29Hz之间，共18个，低频信号间隔为1.1Hz。其时域表达式为：

s（t）=A0cos[2πf0t+g（t）]

g（t）=kf（t）dt（1）

其中f（t）是方波信号，k是移频器的灵敏度因子为常数。

将以上表达式，通过傅里叶级数展开，经过一系列的数学变换后可以导出：

式中：A0为移频信号振幅，f0为移频信号载波频率，m=Δf/f0为信号移频指数，Δf为信号频偏，载波上边频fh=f0+Δf，載波下边频fl=f0+Δf，n为相对于中心频率的频线位置。通过傅里叶级数展开表达式可以看出，移频信号的频谱是以载波频率为中心，以低频信息为间隔向两边对称分布的带通信号。

3采样频率及采样点的确定

ZPW2000移频信号的最大载波频率为2611Hz，根据奈奎斯特定理，采样频率必须大于该频率的2倍。为保证采样结果的高精度，频率的分辨率必须得到保证，但频率分辨率受限于采样频率和采样点，即：

fb=fs/N （3）

由公式可见，要想得到更高的分辨率，则需要更多的采样点，可是对大量的数据进行FFT运算，就会给硬件带来压力。因此，可以通过欠采样技术[2]，在不增加采样点的情况下，降低采样频率，保证频率分辨率。欠采样技术同样遵守奈奎斯特定理，即当带通信号带宽为B=fh-fl时，只要fs?2B，就可以保证采样后的信号频谱不重叠、无失真，采样频率fs需要满足如下关系式：

?fs? （4）

我们将ZPW2000的四种载波频率带入公式（4），确定采样频率，通过计算和筛选可以发现，fs=600Hz时满足ZPW2000移频信号的四种载频的采样需求。

通过欠采样获得的频谱会在N倍的f区域重复出现，所以，我们要确定原信号在哪个区域，通过公式（5）可以得到表1如下：

根据技术要求，低频调制分辨率为0.15Hz，带入公式（3），可以求得采样点需要大于4000个。由于本文使用STM32进行FFT运算，要求采样点必须为4n个，因此规定采样点N=4096个。

4 仿真验证

本文通过MATLAB仿真结果，如下图1所示，图中载频为f0=1700Hz，调制频率为29Hz，频偏Δf=11Hz。采样率fs=600Hz，采样点数为4096个。仿真求得的欠采样后，频率f=99.99，将结果对照表1可知f0=1700.01Hz，1次谐波的频率为f=70.98，由此可知，低频调制频率为29.01Hz。通过仿真结果验证了算法的可行性。

5 系统设计方案

本文采用ST公司的CORTEX-M4系列STM32F407ZET6为处理器，该处理器具有自适应实时加速器（ART），提升了程序执行的效率，同时具备单周期DSP指令和FPU（浮点单元），提升了计算能力。处理器执行速度为210DMIPS/168MHz，并具有三路12位ADC。由于处理器具有以上的硬件特性，保证了系统响应和数据处理的实时性。

本系统通过键盘触发，由单片机对采样数据并进行FFT变换，得到所需测试结果，并通过显示器显示。具体工作流程由下图2所示，系统上电初始化，加载中心频率配置表，随后等待按键触发，若触发便启动定时器，进行高采集频率低采集点的模拟量采集，初步计算出待测FSK的频率，从而确定欠采样对应的中心频率公式，再次启动定时器进行欠采样，将采样结果进行加窗数据处理，对处理后的数据FFT，得出频域数据，算出中心频率和低频调制频率。并将所得结果显示在显示器上。

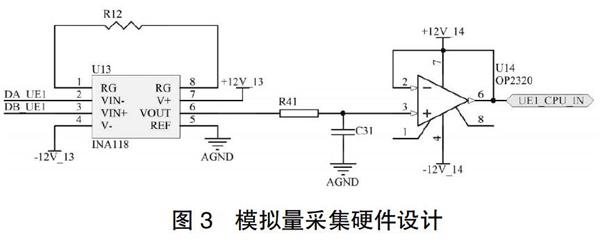
模拟量采集电路如下图3所示，待测信号先通过INA118差分运放，将信号转换成单端信号，再由RC滤波电路滤波，再由OPA2320构成的跟随电路滤波匹配。通过以上的电路进行信号调理，抑制了待测信号中的各种干扰因素，尤其是共模干扰，从而得到高还原的待测信号，保证了测试精度。

6 测试结果

运用设计的测试系统，对通过信号发生器模拟的ZPW-2000A移频信号中的4种中心频率，以及18种低频调制信号进行测试，测试结果见表2。

从测试结果可知，本系统测量中心频率的误差不超过0.2Hz，测量低频调制信号的误差不超过0.04Hz，满足ZPW-2000A移频轨道信号检测误差要求。

7 结论

本文基于欠采样方式对FSK进行采样，对采样结果进行FFT，求出FSK信号的载频以及低频调制频率，经仿真和设计嵌入式系统测量，各项参数指标均达到设计需求。综上可见，通过理论仿真和实际测量结果，证明该测试方法准确度高，外围电路简单，运算速度快，具有较高的实用价值。

【参考文献】

【1】胡广书. 数字信号处理：理论、算法与实现[M]. 清华大学出版社， 2003.

【2】Zhao W L，Giannakis G B，Delic H.Space-time frequency-shift keying[J]. Transactions on Comunications，2004，52（3）：346-349.