平面向星知识点津

端木彦

现实生活中，有些量（如距离、身高、质量等）在取定单位后可以用一个实数来表示，我们称之为数量.但在生活中，我们还会遇到一些不同的量，例如，“飞机从东向西位移30 000 km”，“提起某物体需要300N向上的力”等等.选用合适的数学模型来刻画这些量，继而研究这个数学模型的性质和应用，这些就是《平面向量》一章的内容.本文就其中一些重要知识进行透析.

一、数量与向量的区别与联系

向量可以用有向线段来表示，有向线段的长度表示向量的大小，箭头所指的方向表示向量的方向.不同的是，有向线段具有三个要素：起点、方向和长度.而本章学习的向量是平面内的自由向量，它们仅由方向和大小确定，与起点位置无关.因此，认识向量从它的方向和长度这两个要素人手即可.如“零向量”、“单位向量”，顾名思义，仅规定了大小，方向是任意的.“平行向量”、“共线向量”仅规定了方向，大小是任意的，且因与起点无关，故此二者为同一概念.“相等向量”、“相反向量”则同时对大小和方向提出要求.可见，数量与向量、0与零向量、1与单位向量、平行线与平行向量等概念既有区别义有联系.所以，向量的运算与数量的运算之间必然具有相关性.于是我们进而从代数和几何两个方面研究了向量的加法、减法和数乘这三种运算及其运算律.这三种运算统称为向量的线性运算，它们算的结果都是向量.

二、向量数量积的几何意义

设a，b是两个非零向量，夹角是θ，我们把数量| a | | b | cosθ叫做向量a和b的数量积，记作a.b.数量积满足交换律、数乘结合律和分配律.其中，| b | cosθ叫做向量b在a方向上的投影，它是数量.由此可知a·b的几何意义是：a的长度| a |（如图1中线段OA的长度）与b在a方向上的投影| b | cosθ（如图1中有向线段OB1的数量）的乘积.

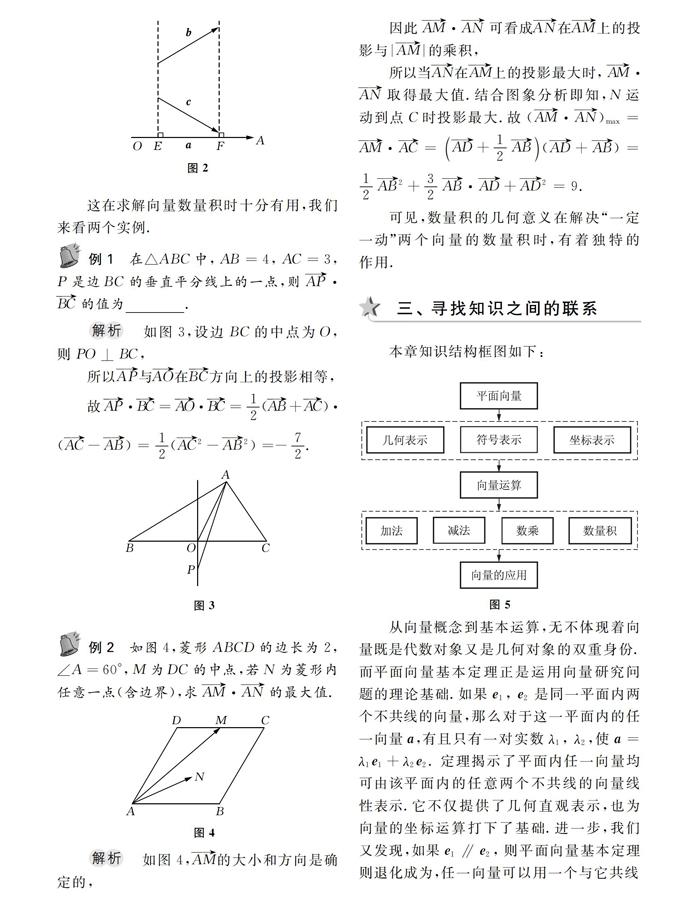
根据数量积的几何意义，我们发现：如图2，如果向量b，c在向量a上的投影相等，则a·b=a·c.

这在求解向量数量积时十分有用，我们来看两个实例.

例1 在△ABC中，AB=4，AC=3，P是边BC的垂直平分线上的一点，则AP·BC的值为__

解析 如图3，设边BC的中点为O，则PO上BC，

所以AP與AO在BC方向上的投影相等，

故AP·BC=AO·BC=1/2（AB+AC）·（AC-AB）=1/2（AC2-AB2）=7/2.

例2 如图4，菱形ABCD的边长为2，∠A=60°，M为DC的中点，若N为菱形内任意一点（含边界），求AM·AN的最大值.

解析 如图4，AM的大小和方向是确定的，

因此AM·AN可看成AN在AM上的投影与| AM |的乘积，

所以当AN在AM上的投影最大时，AM.AN取得最大值.结合图象分析即知，N运动到点C时投影最大.故（AM·AN）max=AM·AC=（AD+1/2AB）（AD+AB）=1/2AB2+3/2AB·AD+AD2=9.

可见，数量积的几何意义在解决“一定一动”两个向量的数量积时，有着独特的作用.

三、寻找知识之间的联系

本章知识结构框图如下：

从向量概念到基本运算，无不体现着向量既是代数对象义是几何对象的双重身份.而平面向量基本定理正是运用向量研究问题的理论基础.如果e1，e2是同一平面内两个不共线的向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1，λ2，使a=λ1e1+λ1e2.定理揭示了平面内任一向量均可由该平面内的任意两个不共线的向量线性表示.它不仅提供了几何直观表示，也为向量的坐标运算打下了基础.进一步，我们又发现，如果e1∥e2，则平面向量基本定理则退化成为，任一向量可以用一个与它共线的非零向量来线性表示，且这种表示是唯一的，即向量共线定理，从这里我们发现，一维情形下的向量共线定理，推广得到二维情形下的平面向量基本定理，今后还能进一步推广得到三维情形下的空间向量基本定理.

借用平面向量的相关知识，我们还将在后续学习中运用向量视角处理三角函数的相关问题.相信在不久的将来，我们也会用向量的眼光观察世界，用向量的语言表达世界，用向量的方法解决现实世界中的一些问题.