基于TSP动态规划的巡查线路排班问题研究
2019-09-10李建军
李建军




摘 要:在很多企业工厂,安排巡检排班都是很重要的一部分,本文将“巡检路线排班最佳”转化为TSP动态规划问题,用贪婪算法分析每班每人近似最佳路线,画出赋权图,然后用C语言编程运行得到可行路线方案,进行均衡度比较从而选定最佳巡查方案。在此基础上考虑错时交班得出遍历图,应用Mathematica编辑对路线进行模拟分析,从而得到人数最少的配置,使人力资源分配更加高效合理。
关键词:TSP动态规划;排班问题;遍历法;均衡度
中图分类号:TP301.6 文献标识码:A 文章编号:2096-4706(2019)01-0155-03
Research on Scheduling Problem of Patrol Line Based on
TSP Dynamic Programming
LI Jianjun
(Department of Basic Sciences,Northern Beijing Vocational Education Institute,Beijing 101400,China)
Abstract:In many enterprises,scheduling of patrol is a very important work. This paper transforms “the best scheduling of patrol route” into the TSP dynamic programming problem. The greedy algorithm is used to analyze the approximate best route of each class,and the weight map is drawn,then the feasible route plan is worked out by C language programming,and the equilibrium degree is compared,so as to select the best patrol plan. On this basis,the ergodic graphcome to consider the staggered office hours,using the Mathematica editor to simulate and analyze the route to obtain the minimum number of configuration,make human resource allocation more efficient and reasonable.
Keywords:TSP dynamic programming;scheduling problem;ergodic method;equilibrium degree
0 引 言
很多工廠企业都有工作站点需要进行巡检以保证正常生产,假设每个点每次巡检需要一名工人,巡检起始地点在巡检调度中心,所有工人可以按固定时间上班,也可以错时上班,在调度中心得到巡检任务后开始巡检。本文通过分析问题建立模型来安排巡检人数和巡检路线,使得所有点都能够按照要求完成巡检,并且耗费的人力资源尽可能少,同时还应该考虑每名工人在一段时间内的工作量要尽量平衡。
首先调查各检查点的巡检周期、巡检耗时两点间的联通关系及行动所需的时间,在不同的条件下,巡检的最少人数及路线。我们将每个检查点看作一个图的顶点,各检查点之间的联通关系看作此图对应顶点的边,各点行走所需的时间看作对应边上的权,这样所给的监察网就转化为了加权网络图。
本问题要针对实际特点寻找通用方法,对于规模较大的问题可使用近似算法来求得近似最优解,故可用TSP动态规划进行分析。
1 涉及数学思想
1.1 TSP动态规划
TSP问题,即旅行商问题,又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求所选择的路径路程为所有路径之中的最小值。旅行推销员问题是图论中最著名的问题之一,即“已给一个n个点的完全图,每条边都有一个长度,求总长度最短的经过每个顶点正好一次的封闭回路”,这类难题有一个值得注意的性质:对其中一个问题存在有效算法时,每个问题都会有有效算法。[1]
1.2 均衡度分析
均衡是平衡的意思,在经济学中,均衡即表示相关量处于稳定值。在供求关系中,某一商品市场如果在某一价格下,想以此价格买此商品的人均能买到,而想卖的人均能卖出,此时我们就说,该商品的供求达到了均衡。[2]
2 合理假设
解决此类问题,要对一些情况进行合理假设:假设巡查人员在各点相遇时互不影响;假设经过不巡查点时不浪费时间;假设巡检员巡检速度为匀速,不会出现特殊情况;忽略天气、故障等因素的影响;假设中午用餐时间为30分钟,每人每天工作8小时;假设工作每天都在循环进行,且工作一致,不存在病假、事假、突发假。
3 问题分析及模型求解
检查路线图,把每个检查点或调度站之间的联通关系看作图中对应节点间的边,任意两点间的间距时间看作对应边上的权,所给的检查路线网就转化为加权网络图。问题研究步骤如下:
(1)用图论软件包求出G中任意两个顶点间的最短路,构造出完备图G'(V,E'),,ω(x,y)=Mind(x,y);
(2)输入图G'的一个初始圈;
(3)用对角线完全算法产生一个初始圈;
(4)随机搜索出G'中若干个初始圈;
(5)对第(2)、(3)、(4)步所得的每个H圈,用二边逐次修正法进行优化,得到近似最佳H圈;
(6)在第(5)步求出的所有H圈中,找出权最小的一个,此即要找的最佳H圈的近似。
二边逐次修正法的结果与初始圈有关,故本算法第(2)、(3)、(4)步分别用三种方法产生初始圈,以保证能得到较优的计算结果。
3.1 工作人员不错时排班统一班次安排
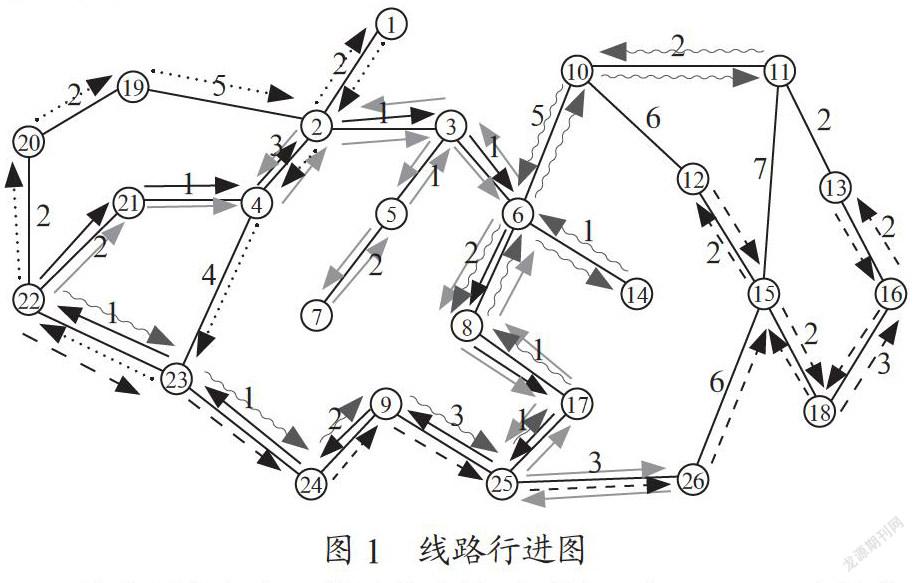
求解算法采用三步完成,第一步,先利用贪婪算法尽量使从调度点出发到各检查点的时间最短;第二步,对各路线的时间再进行调整,进一步优化直到时间不能减少为止;第三步,在保证时间不超过最小周期35分钟情况下对各路线再进行调整直到时间不能缩短为止。针对某一26巡查点工厂,通过C语言程序计算,得到如下线路行进图(如图1所示)。
将此图中各个巡检员的路线历时情况应用Excel表格统计每个巡检员的路线、巡检时间及其路程,从而得到以下线路图和每条线路一圈所需时间,如表1所示。
排班问题考虑工作强度要相对均衡,计算此方案各巡视人员的劳动时间的标准差S:
均衡差异度λ≤30%在合理范围内,我们安排每班5人,24小时需要3班共计15人。考虑到人员上班习惯,方案一巡检时间为第一班,00:00-8:00;第二班,8:00-16:00;第三班,16:00-24:00。
3.2 考虑错时排班优化人力资源配置
采用错时上班,可以更加节省人力资源分配,在此条件下将问题转变为TSP动态规划问题,在MATLAB环境下对迪克斯特拉(Dijkstra)算法编程求出最短路线,并用遍历法得到最优遍历图,再利用Excel表格对数据进行整合分析,与3.1中方案进行均衡度计算与纵向比较。
根据实际工作的经验及上述分析,在分组时应遵从以下准则:
(1)尽量把同一干枝上及其分支上的点分在同一组;
(2)将相邻的干枝上的点分在同一组;
(3)尽量将长的干枝与短的干枝分在一组。
从22点出发去其它点,要使时间较短应尽量走22點到该点的最短间距时间,故用图论软件包求22点到其余顶点的最短间距时间,这些最短间距时间构成一棵22点为树根的树,将从22点出发的树枝称为干枝,如图所示,从22点出发到其它点共有3条枝干,计算出以下遍历图(如图2所示),通过遍历检查得出总时间。
已知每个人工作8小时,一个人走完全程用时136分,列式为:8×60=480分,480/136=3次余72分。
每人(每班四人,每天三班)从22点出发,到下班时间人在16点,并且已巡视完毕,另派两人跟其他人反方向巡检直到到达16点(其中这两人为特殊班次),其中每个人每次巡检时间为64分列式为:64×12=768分,768分=12.8小时。
这种方案中所需人数为:3×4+2=14人。
统计动态班次路线、巡检时间及路程,以12个人为基础班次,后补俩人为特殊班次,这俩人反方向收尾,直到完成所有的检核点的检查,得到时间安排表。如表2所示。
计算此方案各巡视人员的劳动时间的标准差S,从而得到这种动态分配方案的均衡差异度λ为9.2%,由此可知错时上班工作时间的分配方案更为均衡,也更加节省人力,更有效率。
4 模型评价与推广
在排班问题中,本文提出的分组准则简便易行,可操作性强,且可逐步调整使分组达到均衡;排版问题用均衡度的概念定量使得分组方案得到了量化比较;在用近似算法求近似最佳巡检员回路时,采取了两种不同的方法,使得算法比较完善,得到了误差很小的近似最优解。但是,此模型分析将人的因素理想化未考虑路程会影响时间的任何因素,这是日后需完善探索的方向。本模型对交警巡查路线、快递员送件线路、以及便民菜店的设置线路等这些最优化问题提供了可参考分析方案。
参考文献:
[1] Cook W. 迷茫的旅行商:一个无处不在的计算机算法问题:mathematics at the limits of computation [M].北京:人民邮电出版社,2013.
[2] 孙惠泉.图论及其应用 [M].北京:科学出版社,2004.
[3] 朱旭,李换琴,籍万新.MATLAB软件与基础数学实验 [M].西安:西安交通大学出版社,2008.
