考虑多工况和病态载荷的稳健结构拓扑优化设计

陈一雄 赵圣佞 陈成 石军

摘 要：多工况载荷下，结构拓扑优化中的病态载荷问题仍是一个开放的课题。因此，结合变体积约束限技术，构建新的近似拓扑优化模型，提出了一种解决结构柔顺度拓扑优化中病态载荷问题的优化方法。首先，构建多种载荷工况下结构柔顺度的双重凝聚函数，形成新的连续体拓扑优化模型。其次，基于有理分数材料惩罚模型和移动渐近线表示式，形成目标函数和约束函数的显式二次近似式。最后，利用光滑化对偶算法，给出具有收敛性的多工况载荷下连续体结构的柔顺度拓扑优化算法。给出的算例结果表明，与现有方法相比，该方法能解决多工况载荷下结构拓扑优化中的病态载荷问题，且可获得更优和清晰0/1分布的结构拓扑。

关键词：可行域调整;柔顺度优化;结构拓扑优化;多载荷工况

中图分类号：TG156 文献标识码：A 文章编号：1003-5168（2019）01-0037-04

Robust Topology Optimization Design of Structures Considering

Multiple Load Cases and Ill-loaded Problem

CHEN Yixiong1，2 ZHAO Shengning1，2 CHEN Cheng1，2 SHI Jun1，2

（1.School of Automotive and Mechanical Engineering，Changsha University of Science and Technology，Changsha Hunan  410114;2.Key Laboratory of  Lightweight and Reliability Technology for Engineering Vehicle，College of Hunan Province，Changsha Hunan 410114）

Abstract： The ill-load problem of structural compliance topology optimization under multiple load cases still was an opening topic of the structural topology optimization field. Combining with a varied volume limit scheme， a novel approximate model of structural compliance topology optimization under multiple load cases was constructed， and a newmethod called as a duplicate aggregation function method was proposed， which was adopted to solve the ill-load problem of structural compliance topology optimization under multiple load cases. At first， a duplicate aggregation function for structural compliances under multiple load cases was constructed， and a novel approximate topology optimization model was formed. Based on the rational approximation for material properties （RAMP） and the Method of Moving Asymptotes（MMA）， explicitconvex and separable quadratic approximate functions of objective and constraint functions were derived. Then， a compliance topology optimization approach for multiple load cases， possessing convergence， was proposedby adopting a smooth dual algorithm. It was concluded from given examples that the proposed method can solve the ill-load problem of structural compliance topology optimization under multiple load cases， and may obtain a more optimal topology with clear 0/1 distribution than the existed methods.

Keywords： feasible domain adjustment;compliance optimization;structural topology optimization;multiple load cases;ill-loaded cases

在現代工程结构中，常见的一些重要产品结构在复杂载荷工况条件下工作，且载荷工况之间的载荷量级相差很大，甚至在同一载荷工况内，不同结构部位间的载荷量级也存在很大差异。例如，主要的承载机械结构可能需要留有安装传感器的部位或者一些工作平台等，故机械结构除了工作强载荷作用外，还在偏离强载荷作用部位的某处存在小载荷作用。如果小载荷或小载荷工况存在，或者小载荷作用的部位不处于强载荷的传力路径上，那么在基于传统优化方法的多工况载荷下的结构拓扑优化过程中，可能会出现没有材料支承小载荷的优化结构，即所谓的病态载荷。为了解决病态载荷问题，隋允康等根据载荷的量级将载荷分成两个层次[1]，即分别考虑强载荷和弱载荷进行结构拓扑优化设计，最终结果取决于两个层次的划分，且不同载荷的量级差异并不能完全反映它们导致的结构柔顺度的量值差异。James等提出一种结构柔顺度的[η2]范数凝聚方案[η2>1]解决多工况载荷下结构柔顺度拓扑优化问题[2]。Luo也利用结构柔顺度的[η2]范数研究了多刚度优化设计问题[3]。基于不同工况载荷作用的结构柔顺度的量值差异特征，Cai等人考虑从0.1～0.5中取一个小值[η1][4]，形成结构柔顺度的[η1]范数凝聚函数，以解决两组载荷工况下的病态载荷问题。Shi和Cai将该小值[η1]范数的凝聚方案扩展到双模材料的病态载荷工况的结构拓扑优化中[5]。该方法的仿真结果显示，当结构受到超过两组工况载荷作用且这些工况载荷含有病态载荷以及其中的两组大载荷工况的结构柔顺度值相近时，基于小值[η1]范数凝聚方案的结构柔顺度拓扑优化求解只能获得一个较差的局部解。对于仅有两组工况载荷的情况，该方法甚至能解决拓扑优化的病态载荷问题，但难于获得最优解。本文针对含有病态载荷的多工况载荷环境下结构柔顺度拓扑优化问题，提出一种新的优化方法，以解决结构柔顺度拓扑优化的病态载荷问题，获得较好的结构拓扑优化解。

1 含有病態载荷的多工况载荷下结构拓扑优化模型

对于指定体积约束的多工况载荷下结构柔顺度优化问题，实质要求是使[maxl=1，2，…，LClρ]最小。

针对含有病态载荷的多工况载荷环境下结构柔顺度拓扑优化问题，本文构建式（1）的结构柔顺度的双重凝聚函数[faggρ]，并将它作为多工况载荷环境下结构柔顺度拓扑优化模型的近似目标函数。

[faggρ=l=1LClρClmρ0η1η2η1+l=1LClρClmρ0η11η2]（1）

式中，L表示载荷工况总数，[Cl]表示第l组工况载荷作用下的结构柔顺度，[lm]为最大初始结构柔顺度值[Clmρ0]对应的载荷工况序号，[η1]和[η2]为经验参数，分别取小于1和大于1的值。因此，本文基于最大结构柔顺度最小和预定结构体积要求，构建了多工况载荷环境下结构柔顺度拓扑优化模型：

[minfaggρ=l=1LClρClmρ0η1η2η1+l=1LClρClmρ0η21η2s.t.   q=1QρavnqV0nq+p=1pραvipV0iq/V0≤V*/V0Kρulρ=Fl，l=1，2，…，Lρminnq≤ρnq≤1，q=1，2，…，Q]（2）

式中，[V*]表示约束的体积值，[V0]为初始结构的体积值，而K表示结构总刚度阵。[Fl]为第l组工况载荷，[ul]为第l组载荷工况下结构的位移响应。取[ρminnq=10-5]，以避免结构总刚度阵奇异。

2 结构柔顺度的灵敏度分析和多工况载荷下结构拓扑优化近似模型

引入如式（3）、式（4）所示的变体积限技术：

[Vk+1u=Vk-minβ1V0，V*-Vk，Vk≥V*Vk+minβ1V0，V*-Vk，Vk<V*   ，k=1，2，3]（3）

[Vk+1U=maxVkU-β1V0，V*，V4≥V*minVkU+β1V0，V*，V4<V*   ，k=4，5，…]（4）

式中，[β1]为经验参数，取值范围为[0.005，0.025];[Vk]表示第k迭代步的结构体积;[λk]是前一步（第k步）的拉格朗日乘子。

式（4）中，[Vk+1U]相对于迭代步k是单调变化的。在进行有限迭代步后，式（2）的可行域完全与优化模型（4）的可行域一致。式（2）的收敛性完全由求解算法确定。另外，变体积约束限技术的引入使得近似优化模型（2）易于用对偶方法求解，且基于措施的优化方法可获得序列清晰拓扑。

再者，类似于文献[6，7]，将人工变量[w1]引入到模型（2），至此得到拓扑构型可稳健变化的优化模型（5）。

[minfk0ρ+c1w1+12d1w21s.t.   fk1ρ-w1≤0ρ∈ρk，w1≥0]                  （5）

3 算例

图1左端固定的悬臂梁尺寸为2m×1m×0.002m，其弹性模量和泊松比分别为200GPa和0.3。作用于结构的三组工况载荷都为集中载荷工况。工况载荷一的集中载荷[F1]为8 000N，沿铅垂方向向下作用于结构的右端中点。工况载荷二的集中载荷[F2]为10N，沿铅垂方向向下作用于结构的右端上端点。工况载荷三的集中载荷[F3]为10 000N，沿铅垂方向向下作用于结构的上边中点。将初始设计域划分为等尺寸的5 000个平面应力单元，并指定目标体积比[θ=0.4]。本文取长度过滤尺寸为[rmin=3.0Δmin]（[Δmin]是结构单元边长的最小尺寸）。初始设计结构的拓扑变量都为1.0。收敛参数取为[ε1=0.000 1]和[ε2=0.000 1]。双重凝聚函数的两个参数[η1]和[η2]分别取0.2和10。

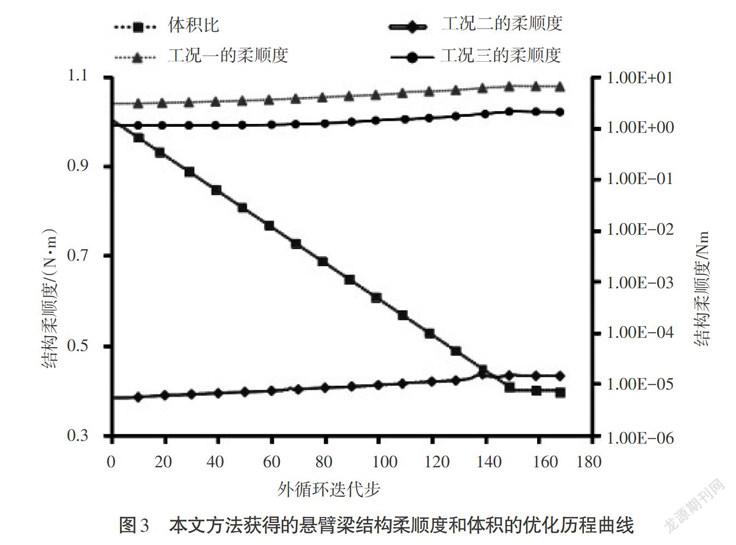
图2为本文方法获得的悬臂梁结构拓扑优化历程图。可以看出，尽管载荷的量级相差非常大，在最后的构型中仍然有材料支撑弱载荷，可获得较好的拓扑优化解。这充分说明本文方法是有效的，能够解决病态载荷问题。图3给出了本文方法获得的悬臂梁结构的结构体积比和各工况载荷下结构的柔顺度的优化历程曲线。不难看出，整个优化历程是稳健变化的。

4 结论

本文提出了解决病态载荷问题的一种新的多工况载荷下连续体结构的柔顺度拓扑优化求解方法。从方法的理论公式和给出的算例可以得出以下结论：①提出的结构柔顺度拓扑优化方法能解决病态载荷问题，且具有收敛性和好的稳健性;②本文方法可获得更优、更清晰0/1分布的优化结构拓扑。

参考文献：

[1]隋允康，彭细荣，叶红玲.ICM应力全局化方法克服连续体拓扑优化的载荷病态[J].工程力学，2009（6）：1-9.

[2]James K A，Hansen，Jorn S，et al.Structural Topology Optimization for Multiple Load Cases Using a Dynamic Aggregation Technique[J].Engineering Optimization，2009（12）：1103-1118.

[3]Luo Z，Chen L P，Zhang Y Q，et al.Multi-stiffness Topological Optimization for Continuum Structures with Multiple Loading Cases and a Duplicate Sensitivity Filtering Method[J].Acta Mech Solida Sin.，2005（1）：29-36.

[4]Cai K，Shi J，Zhang A.Stiffness Design of a Continuum Under Ill-load Cases by Fractionalnorm Objective Formulation[J].Optimization and Engineering，2014（4）：927-944.

[5]Cai K，Cao J，Shi J，et al.Optimal Layout of Multiple Bi-modulus Materials[J].Struct. Multidisc. Optim.，2016（53）：801-811.

[6]Groenwold A A，Etman L F P，Wood D W.Approximated Approximations for SAO[J].Structural and Multidisciplinary Optimization，2010（1）：39-56.

[7]Etman L F P，Groenwold A A，Rooda J E. irst-order Sequential Convex Programming Using Approximate Diagonal QP Subproblems[J].Structural and Multidisciplinary Optimization，2012（4）：479-488.