桥梁斜截面抗剪工况静载试验计算分析

蒋凌杰 吴志隆 吴维彬

摘要：文章以实际工程桥梁静载试验为例，介绍支点附近斜截面抗剪工况的静载试验方法，对比采用Midas杆系模型和Ansys实体模型计算的斜截面应力理论值，结合静载试验的实测数据分析和理论数据分析，得到斜截面抗剪工况理论值。经计算发现，采用杆系模型计算的结果存在较大偏差，会造成静载试验的评定结果不合理。因此，进行支点附近斜截面抗剪工况理论应变计算时应采用实体模型。

关键词：静载试验;斜截面抗剪;荷载试验效率;实体模型;校验系数

中图分类号：U442 文献标识码：A 130I：10.13282/j.cnki.wccst.2019.10.026

文章编号：1673-4874（2019）10-0090-03

0 引言

桥梁荷载试验是评定桥梁整体承载能力的直接而重要的手段，而桥梁静载试验是荷载试验的主要内容之一，通过静载试验可以评定结构的整体强度、刚度等。对于简支桥梁的静载试验，主要试验工况为跨中截面最大正弯矩工况，附加工况为支点附近截面抗剪工况。通过试验结果分析得到各工况下荷载试验应变校验系数和挠度校验系数，以此综合评定结构的承载能力是否满足相应荷载等级的要求。

结构计算分析是桥梁荷载试验的核心工作，准确的结构计算是保证荷载试验评定结果准确性的基础。静载试验的计算内容主要包括荷载试验效率的计算和理论效应值（应变及挠度）的计算。对于跨中截面最大正弯矩工况，常规桥梁静载试验采用杆系模型即可满足计算精度的要求，同时又兼顾经济性。对于附加试验工况支点附近截面抗剪工况，对截面斜向应变的计算，采用杆系模型进行计算可能存在较大的误差，因此需要分析该工况下单独采用杆系模型进行计算的适用性。

本文试验对象为某加固工程更换上部结构的简支桥跨，更换的上部结构为跨径16m的装配式预应力混凝土小箱梁，小箱梁采用C50混凝土，橫向布置5片，湿接缝连接，桥墩为双柱式桥墩，桥面铺装为水泥混凝土，桥面净宽为8.0m。本桥是利用部分原结构的加固工程，桥梁加固后的设计荷载采用原汽车荷载等级为汽车-超20级。

1荷载试验实施步骤

1.1荷载试验效率

确定荷载试验荷载等级后，可根据设计标准荷载产生的最不利效应值作为控制效应，通常控制效应采用内力效应值，根据确定的控制内力效应值，在给定的荷载试验效率范围下，采用影响线加载的方法反算得到试验所需加载车辆的数量及加载位置。一般新桥的静载试验荷载效率取值为0.85-1.05，旧桥静载试验荷载效率取值为0.95-1.05。

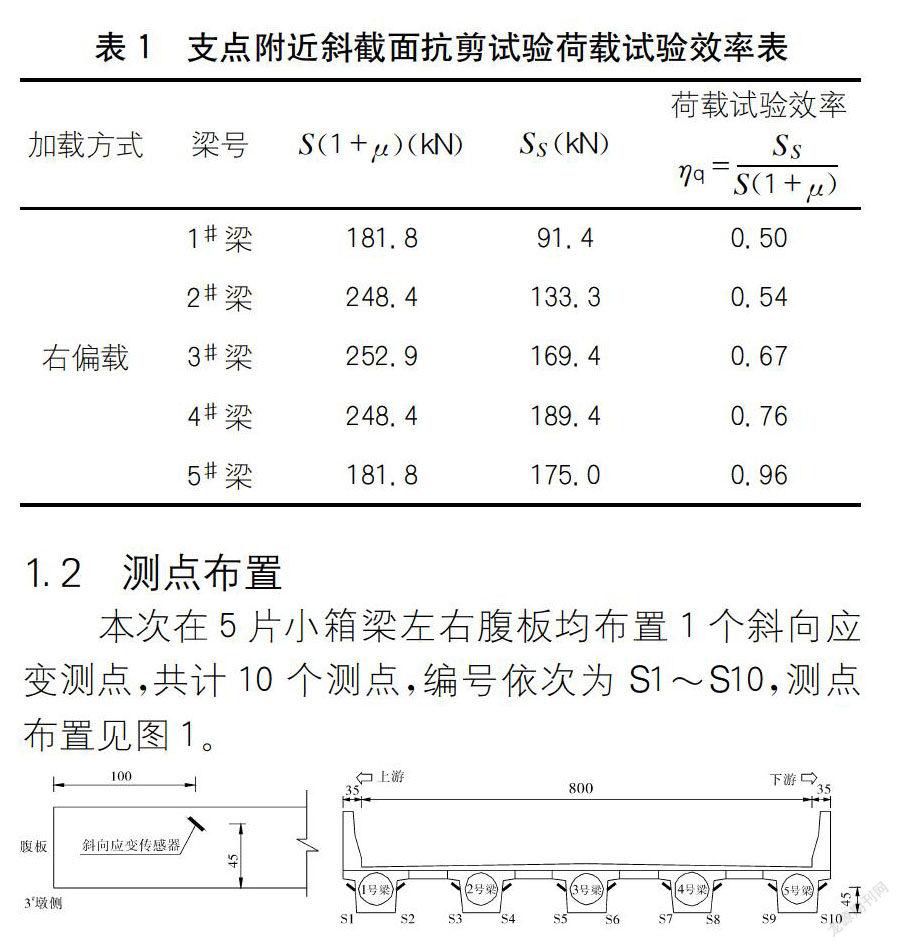
本桥试验跨横向布置为5片梁，采用单梁杆系模型计算结构在汽车荷载作用下的效应值乘以各梁的横向分布系数得到每片梁的设计汽车荷载效应S，依据结构基频计算冲击系数μ，采用影响线加载计算每片梁的试验荷载效应S。经计算，本次试验采用4辆34t车辆加载，荷载试验效率达到0.96，可满足规范要求。各梁的荷载试验效率结果如表1所示。

1.2 测点布置

本次在5片小箱梁左右腹板均布置1个斜向应变测点，共计10个测点，编号依次为S1-S10，测点布置见图1。

1.3试验加载布置

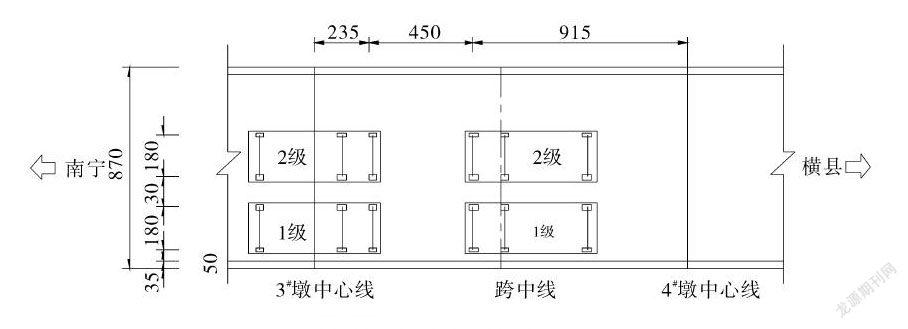
静载试验工况为不利的偏载工况，试验采用2级加载和1级卸载。加载程序如下：

（1）加载前，将加载汽车过地磅称重，满足试验要求车重后进行加载。

（2）正式加载前，对试验跨进行预压，预压后进行第一次空载读数，同时记录该时刻的气温。

（3）正式实施试验加载，每级汽车荷载驶入指定的区域就位后，稳定15min记录加载后开始试验观测第一次读数，间隔10min再记录加载的第二次读数，两次读数差均小于前次读数增量的10%时，认为结构变形已趋稳定。此时所记录的数据为试验实测数据。

（4）满载完成后进行一次卸载，稳定20min后观测应变数据。加载布置见图2。

2 测点斜截面应力理论值计算

校驗系数是反映桥梁结构实际状况与理想状况的偏差、确定结构承载能力的重要指标。静载试验中，通过试验荷载作用下的实测应变值和理论应变值，计算应变的比值确定校验系数，理论应变值计算的准确性是关键。

对于支点附近斜截面抗剪工况下测点斜向应变值，采用常规杆系模型计算截面位置主应力，再按照横向分布系数来计算各个梁的斜截面应变值;而采用实体模型直接确定各个测点位置的斜向应变值。采用Midas Civil建立的杆系模型和ANSYS建立的实体模型见图3-4，测点斜向应变计算结果对比见表2。

表2数据显示，满载工况下，采用杆系模型计算结果和实体模型计算结果存在差异：非偏载側梁斜向应变值，两者应变值大小差异明显，测点应力类型也有不同，偏载側梁的斜向应变值差异较小，偏差率在20%内，试验控制梁的偏差值最小。

3 静载试验结果对比分析

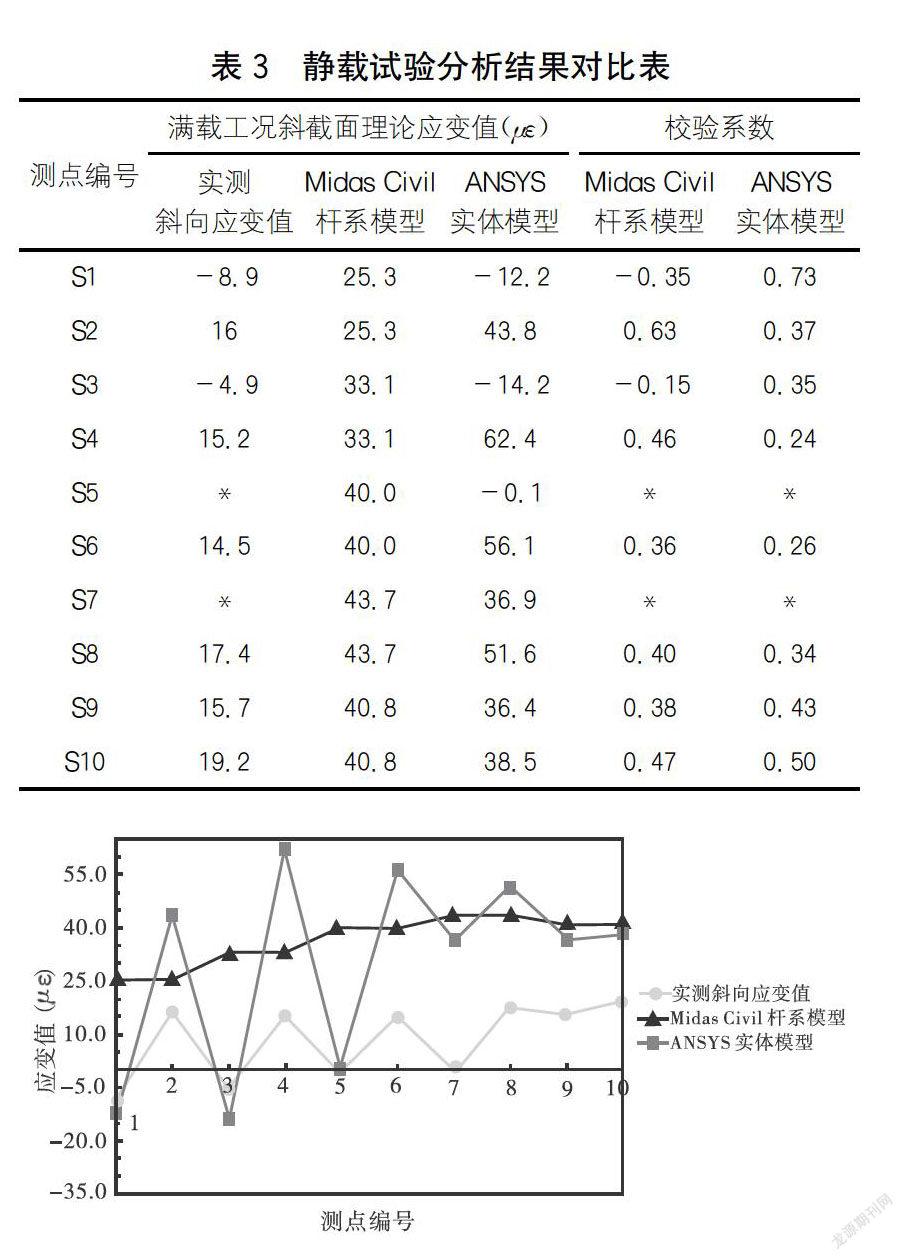
对某加固工程试验桥跨进行了支点附近斜截面抗剪工况试验，试验工况为偏载工况，静载试验应变测试结果分析见表3，实测应变及理论应变对比分析见图5。

测试结果表明：

（1）实测应变结果与实体模型计算结果较为吻合，采用实体模型理论应变值计算的应变校验系数结果合理。

（2）杆系模型计算结果在#-3#梁左右测点应力状态与实测不一致。导致采用杆系模型计算的理论值进行应变校验系数计算时，校验系数存在负值，结果不合理。而偏载側的4*-5*号梁采用两种模型理论值计算的测点校验系数结果偏差相对较小。

（3）结合荷载试验实测的斜截面应变结果分析可知，实体模型应变理论值与实测值较为吻合，各个测点按照实体模型计算的校验系数均合理，表明在进行支点附近斜截面抗剪工况时，应采用实体模型进行理论值计算。

4 结语

本文以某工程桥梁荷载试验为依托，介绍了桥梁静载试验的基本步骤和分析方法，文中对比分析了基于杆系模型程序计算的斜截面理论值和实体模型计算的理论值，认为两者计算结果有一定的偏差，尤其在非偏载側的测点斜向应力计算结果存在明显的差异。结合静载试验实测的应变数据可知，实体模型计算各梁的应变结果与实测结果相吻合，分析得到的应变校验系数合理;而采用常规杆系模型计算各梁的应变结果进行分析时，会导致计算的校验系数结果不合理，尤其在非偏载側结果偏差大。因此，在进行支点附近斜截面荷载试验抗剪工况时，应采用实体模型计算斜截面应变理论值。本文通过对该桥梁进行静载试验理论分析和现场试验，为同类桥梁静载试验提供参考。