防城港进港航道工程平面二维潮流数学模型适用性分析

摘要：根据防城港码头规划布置，防城港渔澫港区第五作业区进港航道工程提出了将进港航道分为5万吨级和3万吨级两段不同吨级的航道进行合理设计的方案，以满足岸线码头的配套服务要求。文章根据防城港工程海域相关的地质及水文条件，建立了平面二维潮流数学模型，确定了模型的初始条件、边界条件及模型参数，并通过实测数据验证了该模型在防城港海域的适用性及所建立模型的正确性。

关键词：防城港;渔澫港区;航道设计;二维潮流模型

中图分类号：U611 文献标识码：A DOI：1 0.1 3282/j. cnki. wccst. 2019. 12. 049

文章編号：1673 - 4874（2019）12 - 0185 - 04

0 引言

近年来，随着西部大开发的深入实施、泛珠三角区域合作进一步加强、中国一东盟自由贸易区和“一带一路”建设不断推进以及广西北部湾经济区和东兴重点开发开放试验区的建设上升至国家发展战略层面，防城港迎来了前所未有的发展机遇。由于船舶的大型化，港口规模的扩大化，使得原本就交通紧张的港口水域航道要承受更大的压力，这就迫使港口水域航道需要重新规划、升级，以缓解当前的通航压力，并满足未来发展的需要。航道作为港口水域布局的一个重要方面，其规划的合理性对提高港口水域通航安全和效率有很大作用。

防城港岸线资源总量有限，潮流动力环境较复杂，新航道的建设涉及航道通航代表船型、通航尺度、平面布置、防淤减淤等问题，尚需进行一定的基础研究工作。在投资尽可能少、工程量尽可能小的前提下，据防城港港口总体规划中关于渔澫港区第五作业区的泊位建设情况及航道工程设计相关规范，对防城港渔漓港区第五作业区进港航道工程提出了将进港航道分为5万吨级和3万吨级两段不同吨级的航道进行合理设计的方案，需要对相应的进港航道方案进行数值模拟研究，以满足岸线码头的运作要求。本文将根据防城港工程海域相关的地质及水文条件，确定模型的初始条件、边界条件及模型参数，通过建立平面二维潮流数学模型，验证该模型在防城港海域的适用性及所建立模型的正确性。

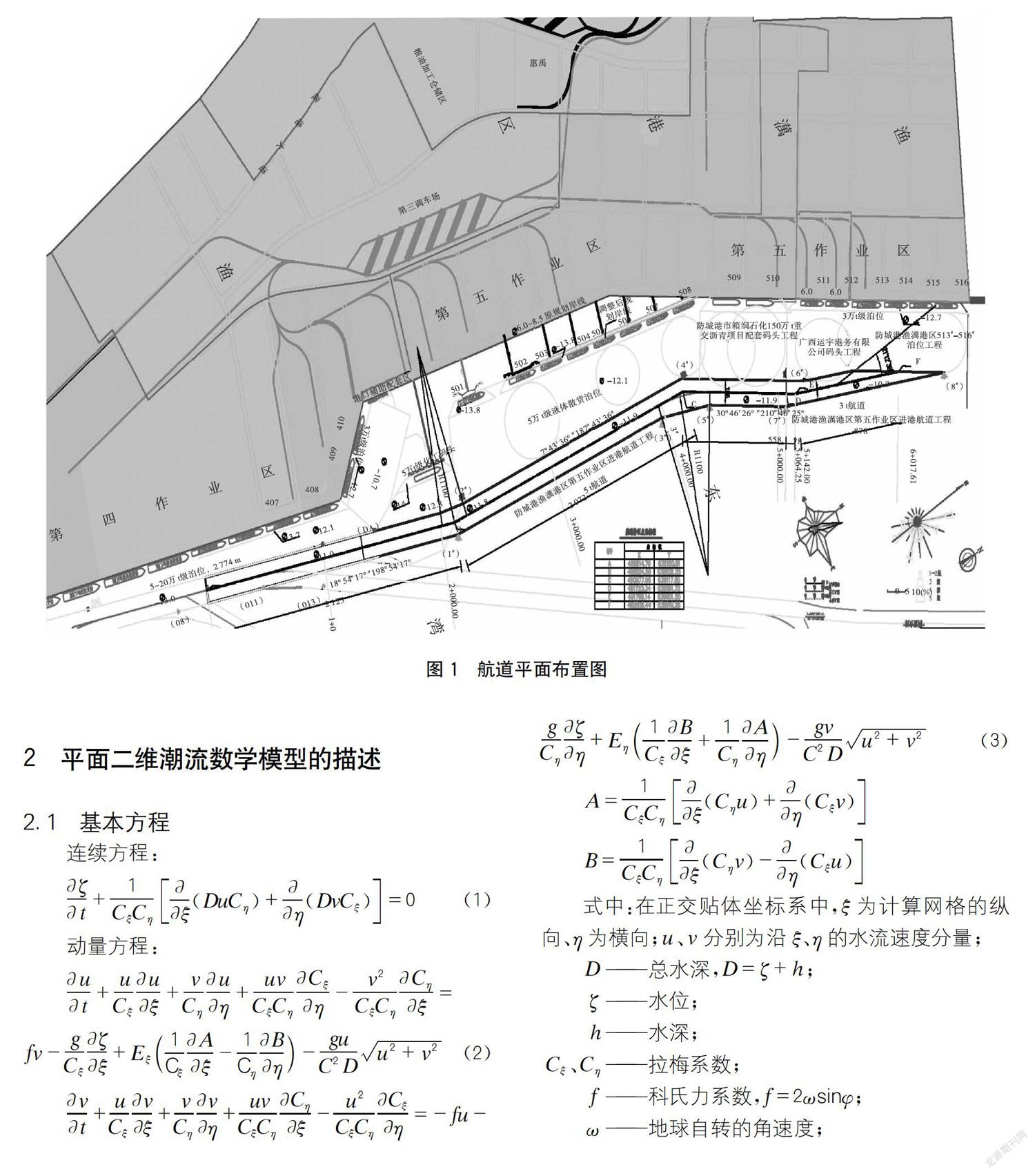
1 防城港渔澫港区第五作业区进港航道工程设计方案

设计方案以防城港港区的地质地貌、水文气象等资料为基础，在研究防城港未来到港船型预测的基础上，结合相应的参考技术标准及设计原则，根据第五作业区沿岸码头布置情况及工程海区水深地形条件，并考虑大型船舶航行安全，尽量保证航道轴线顺直，避免多次转向，尤其是大角度转向。

设计进港航道长为6 018 m，航道起点位于渔漓港区已建成的5万～10万吨级东湾航道起点A处，终点位于防城港渔澫港区第五作业区北端513#～516#泊位回旋水域外边线中段F点。从航道的起点A到510#泊位北侧的AE段设计为长5 064 m的5万吨级进港航道，设计通航宽度为156 m，底标高为- 11. 90 m;511 #泊位南测至516#泊位回旋水域中段的EF段设计长为954 m的3万吨级航道，设计通航宽度为128 m，底标高为- 10. 70 m。

航道具体走向为：从起点A顺现有5万～10万吨航道2 125 m至液体化工码头北侧港池边界B点;从B点向北偏沿7。43'36"延伸2 072 m到C点;从C点向东偏沿30。46 725”延伸868 m到D点，形成5万吨级航道;从D点向东偏沿21°12'38"延伸954 m至F点，形成3万吨级航道。航道全长6 018 m，见图1。

2.3 数值计算方法

对上述微分方程进行离散计算时，时间项运用向前差分计算的格式，空间项运用中心差分计算的格式。

数值求解用ADI法（戴贤凯等，1987），此方法中涉及的网格划分方法、差分算法等详见《海岸与河口潮流泥沙模拟技术规程》。这一方法的优点是计算原理已非常成熟完善且运用广泛，它的求解速度快，求解过程较为稳定。ADI法的求解原理是：求解中将一个时间步长分两个半步来计算，前半步采用隐式求解ξ方向的流速分量和潮位，显式法求解流速在7方向的分量;后半步则反过来，采用隐式求解η方向流速分量和潮位，显式法求解流速在ξ方向的分量。

3计算范围确定及网格剖分

模型范围计算域覆盖了防城港两个内湾及防城港规划20万吨级航道（理论基面-18 m）水域。计算域的长宽分别为42 km和27 km。运用正交曲线网格，网格总数为358×229，在工程区位置需要将网格加密提高精度，外海网格较疏，空间步长最短为8.8 m，最长为549.8 m，工程区水域网格尺度约为30 m。

4 参数处理

4.1 动边界处理

计算海域内有边滩和浅滩分布，要想在计算时将边滩和干湿特征体现出来，就要对动边界做一些特殊的处理。

本文中选择冻结法对动边界进行处理。冻绪法的基本原理是：若节点的水深小于设定的控制值，将该点潮位值的大小“冻结”，使其不参与计算，在计算后一时刻前，用周边节点的水深值对被冻结的节点水深进行修正;若节点水深值大于设定的控制水深时则正常参与计算。这里将动边界的控制水深设置为5 cm，尽量不引起数据计算失真。

4.2 糙率选取

在进行潮流模拟计算时，糙率n是一个重要的综合性参数，能深度影响到模拟结果的准确性与正确性。糙率实际上代表着潮流运动时所受到的阻力特征，它的大小和海底床面的泥沙性质、水深大小、水下地形均有关系，本文通过以下公式进行计算：

n= n0 +n’/H

（8）

式中，no是基础糙率，结合在防城港和钦州湾海域的计算经验取为0. 015～0. 020，基础糙率较大值一般出现在红树林区及岛群区域;n'/H为糙率修正项，n取0. 012。特别要注意的是，若水深H<1 m，个别点处糙率可取0. 032，若水深在≥1 m则直接用式（8）加以修正。

4.3 其它参数

另一个重要的参数是与网格大小和潮流相关的紊动黏性系数，此参数若取值恰当则计算结果精度更高。根据Smagorinsky（1963）所述方法，可使紊动黏性系数根据网格的大小和潮流强弱自适应，能够保证计算结果的真实性，提升计算过程的稳定性。各参数取值如表1所示。

4.4 数学模型验证

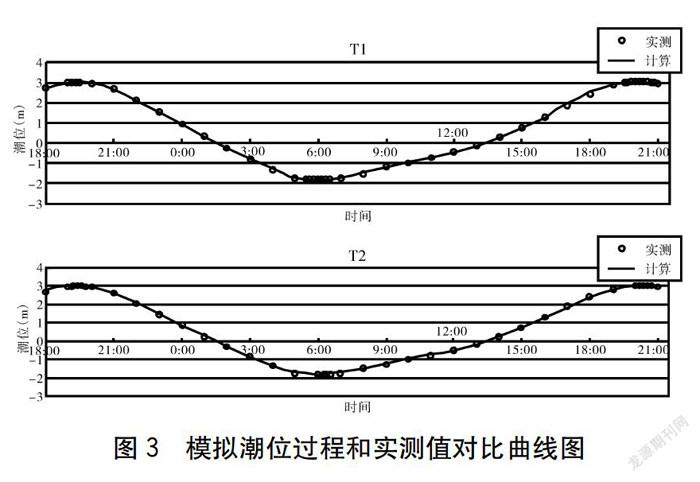
防城港潮流主要是全日潮，这里利用2007 -05 - 19～20防城港监测的大潮数据对模型加以验算，所选流速及潮位测点如下页图2所示，其中V7、V8为流速测点，T1、T2为潮位测点。

图3展示了二维潮流模型模拟的潮位过程与实测值。从图中可以看出，模型的模拟结果和实测数据的变化趋势基本一致，高潮位和低潮位的数值也较为贴切。这体现出对于防城港水域所建立的模型恰当，平面二维潮流模型所计算的结果与实测的潮流动力基本一致，计算中所设置的模型边界条件是正确的，网格划分是合理的。

图4展示了各测点的流速、流向模拟值与现场实测数据之间的对比结果。从图中可以看出，该模型模拟得到的潮流流速、流向和现场实测的数据均是比较贴切的，因此验证了所建立模型的适用性和正确性，模型计算中所选取的各项参数是适合且可靠的，可利用该平面二维潮流模型进行新建航道的设计研究工作。

5 结语

本文对防城港拟建航道海域建立了平面二维潮流模型，介绍了所建模型的方程及求解條件、计算方法、网格划分及参数选取处理等方面内容，并验证了该模型在防城港海域的适用性及参数选取、网格划分的合理性。平面二维潮流模型计算结果有较好的可信度，为该航道设计方案的数值研究打下了基础，可为该类多吨级航道方案的设计及实际工程建设提供借鉴和参考。

同时，由于三维潮流模型在研究边界变化较为剧烈的区域具有较好优势及准确性，随着数值模型的深入研究及计算机技术的不断进步，未来三维潮流模型在港口航道工程中的应用具有良好的前景，这方面值得进一步深入研究。本次主要针对新建航道设计方案开展了数学模型的建模分析，其模拟结果的准确性相对有限，未来可进一步建立包括码头、港池、锚泊地、回旋水域等在内的全面数学模型进行模拟验证，提高计算结果的准确性。

参考文献

[1]广西交通规划勘察设计研究院有限公司.防城港港口总体规划（2016 - 2030）[R].2017.

[2]于家根.港口水域航道合理规划设计研究[D].大连：大连海事大学交通学院，2008.

[3]孙平峰.椒江口二维潮流泥沙数学模型研究[D].杭州：浙江大学建筑工程学院，2006.

[4]李世森，时钟.河口潮流垂向二维有限元数学模型[J].海洋科学，2001，25（9）：39 - 44.

[5]戴贤凯，田海勇，刘家驹.北仑港区潮流数值计算和>中淤分析[J].海洋工程，1987（4）：51 - 62.

作者简介：徐思思（1987-），工程师，主要从事港口规划建设管理工作。