基于PID算法对智能车自动控制的研究与实现
2019-09-10陶文鹏
陶文鹏


摘 要:本设计以摄像头为传感器,利用电机和舵机来控制智能车的方向及速度,旨在研究并实现PID控制算法。其间设计并建立了简略的数学模型,进行相应数学公式的推导,同时通过相关软件进行仿真,结合实际参数,研究PID算法的原理。其目的是将PID算法与智能车车模相结合,使智能小车能够正常并稳定地沿着路径行驶。
关键词:智能车;PID算法;路径循迹;软件仿真
中图分类号:TP242.6 文献标识码:A 文章编号:1003-5168(2019)19-0030-03
Abstract: This design took camera as sensor, used motor and steering gear to control the direction and speed of intelligent vehicle, aiming at researching and realizing the PID control algorithm. In the meantime, a simple mathematical model was designed and established, and the corresponding mathematical formula was deduced. At the same time, the principle of the PID algorithm was studied by simulation with relevant software and actual parameters. Its purpose is to combine the PID algorithm with the intelligent vehicle model, so that the intelligent car can travel along the path normally and steadily.
Keywords: intelligent vehicle;PID algorithm; path tracking;software simulation
智能车作为轮式机器人的一个分类,在如今大数据与人工智能的时代背景下,其应用较为广泛,智能化需求日趋强烈,而控制系统是智能车的“智能”体现之处。基于自带的硬件与传感器,智能车要实现自动控制与行驶的能力,还需要相应的控制算法。智能车控制是一个既关键又复杂的问题,需要考虑到道路形状和智能车自身等各种因素的影响[1]。最基本的控制方式是开环控制,通过传感器收集路径信息,直接控制舵机进行打角,最终控制智能车的方向。其缺点十分明显,基于开环控制的智能车速度是固定不变的,不能随着路况改变,其稳定性在遇到类似急转弯的特殊路径时不能得到保证。而PID控制算法采用的是闭环控制方式,通过反馈方式,调节相关参数,使智能车能够稳定并以较快的速度进行自动循迹。
1 PID控制算法原理
PID控制器由以下几个单元构成,即比例单元(P)、积分单元(I)和微分单元(D)[2]。系统的输入[e(t)]和输出[u(t)]的关系为:
(1)
式中,[KP]为比例系数;[TI]为积分时间常数;[TD]为微分时间常数;0和[t]分别为积分的上下限。
分别决定着各个控制单元的控制能力强弱。对[u(t)]和[e(t)]进行拉普拉斯变换,整理可得,PID调节器的传递函数为:
(2)
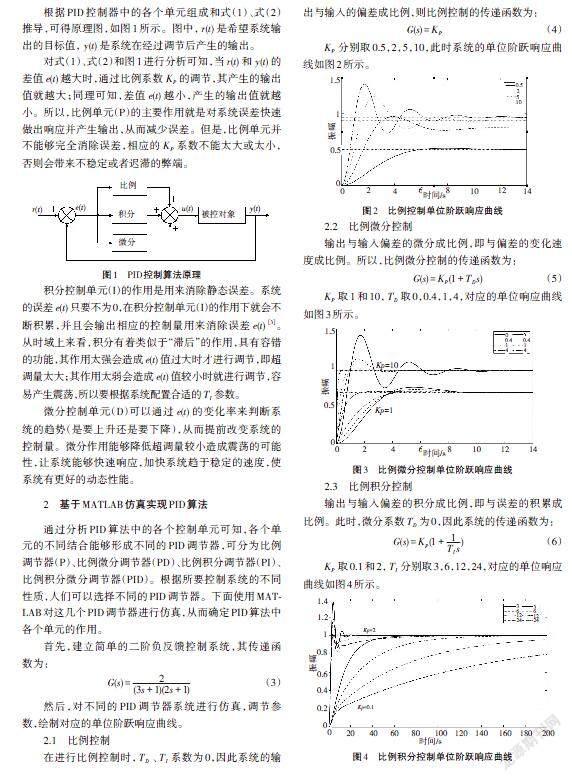
根据PID控制器中的各个单元组成和式(1)、式(2)推导,可得原理图,如图1所示。图中,[r(t)]是希望系统输出的目标值,[y(t)]是系统在经过调节后产生的输出。
對式(1)、式(2)和图1进行分析可知,当[r(t)]和[y(t)]的差值[e(t)]越大时,通过比例系数[KP]的调节,其产生的输出值就越大;同理可知,差值[e(t)]越小,产生的输出值就越小。所以,比例单元(P)的主要作用就是对系统误差快速做出响应并产生输出,从而减少误差。但是,比例单元并不能够完全消除误差,相应的[KP]系数不能太大或太小,否则会带来不稳定或者迟滞的弊端。
积分控制单元(I)的作用是用来消除静态误差。系统的误差[e(t)]只要不为0,在积分控制单元(I)的作用下就会不断积累,并且会输出相应的控制量用来消除误差[e(t)][3]。从时域上来看,积分有着类似于“滞后”的作用,具有容错的功能,其作用太强会造成[e(t)]值过大时才进行调节,即超调量太大;其作用太弱会造成[e(t)]值较小时就进行调节,容易产生震荡,所以要根据系统配置合适的[TI]参数。
微分控制单元(D)可以通过[e(t)]的变化率来判断系统的趋势(是要上升还是要下降),从而提前改变系统的控制量。微分作用能够降低超调量较小造成震荡的可能性,让系统能够快速响应,加快系统趋于稳定的速度,使系统有更好的动态性能。
2 基于MATLAB仿真实现PID算法
通过分析PID算法中的各个控制单元可知,各个单元的不同结合能够形成不同的PID调节器,可分为比例调节器(P)、比例微分调节器(PD)、比例积分调节器(PI)、比例积分微分调节器(PID)。根据所要控制系统的不同性质,人们可以选择不同的PID调节器。下面使用MATLAB对这几个PID调节器进行仿真,从而确定PID算法中各个单元的作用。
首先,建立简单的二阶负反馈控制系统,其传递函数为:
(3)
然后,对不同的PID调节器系统进行仿真,调节参数,绘制对应的单位阶跃响应曲线。
2.1 比例控制
在进行比例控制时,[TD]、[TI]系数为0,因此系统的输出与输入的偏差成比例,则比例控制的传递函数为:
(4)
[KP]分别取0.5,2,5,10,此时系统的单位阶跃响应曲线如图2所示。
2.2 比例微分控制
输出与输入偏差的微分成比例,即与偏差的变化速度成比例。所以,比例微分控制的传递函数为:
(5)
[KP]取1和10,[TD]取0,0.4,1,4,对应的单位响应曲线如图3所示。
2.3 比例积分控制
输出与输入偏差的积分成比例,即与误差的积累成比例。此时,微分系数[TD]为0,因此系统的传递函数为:
(6)
[KP]取0.1和2,[TI]分别取3,6,12,24,对应的单位响应曲线如图4所示。
2.4 比例积分微分控制
比例积分微分控制即为PID控制,传递函数为:
[G(s)=KP(1+1TIs+TD·s)] (7)
取适当的[KP]=100,[TI]=2.2,[TD]=7,绘制系统的单位阶跃响应曲线,人们可以发现系统能够在较短的时间达到稳定,其单位阶跃响应曲线如图5所示。
对几个仿真的公式及图像结果进行分析,可以归纳出各个PID调节器的特点。
2.4.1 比例控制。P调节器控制可以消除扰动的影响,能以较快的速度作用于输出值,但是不能完全消除误差。[KP]值过大,易产生波动;[KP]值太小,响应速度太慢。
2.4.2 比例积分控制。PI调节器在比例P的基础上以积分作用消除余差,因为积分的作用效果有一定的迟滞性,所以适用于误差[e(t)]变化不大且对被控参数的精度有较高要求的场合。
2.4.3 比例微分控制。PD调节器在微分的作用下有着很好的预测性,对于具有一定容量滞后的控制系统,设置适当的[TD]参数,可以显著地提高系统的动态性能指标。
2.4.4 比例积分微分控制。PID调节器是一种较为理想的控制方式,在比例P的基础上引入微分作用,可以消除余差,再加上微分作用,又能提高系统动态响应速度和稳定性[4]。由于PID调节器存在积分作用,因此PID调节器有着一定的时间滞后,对于要求响应速度较快的系统,需要适當调节[TI]参数,或者只使用PD调节器。
3 PID算法的实现
3.1 智能车设计主要模块
3.1.1 处理芯片模块。作为整个智能小车的“大脑”,收集来自传感器的数据,处理收集到的信息,结合PID算法对电机和舵机的输出进行控制。
3.1.2 传感器模块。智能小车使用的是OV7725摄像头,对路径图像进行二值化处理,形成对应的黑白图像,处理芯片计算得到路径中心值,确定小车方向的偏差值,从而寻找路径的中线进行自动循迹。
3.1.3 驱动模块。小车具有4个轮子,后面2个轮子配有2个电机,其可以通过调节电机输入的PWM波的占空比来控制智能车的速度,前面2个轮子由一个舵机控制,舵机打角来控制智能车的方向。
3.1.4 速度检测模块。为了使用闭环控制,智能小车的车模后轮附加了编码器,后轮的转动会带动编码器的转动,从而产生输出脉冲信号,处理芯片通过对脉冲信号正交解码对智能车进行测速,测得的速度作为速度调节的反馈输入。
3.2 基于PID算法实现智能车的自动控制
3.2.1 速度控制。智能小车自动循迹期间存在不同的路况。在直道上行驶,路径中心与小车中心的偏差较小,因此可以给智能车一个较快的速度,同理在弯道上偏差较大,可以给智能车一个较慢的速度。根据智能车速度调节的特点,不同的路段保持速度稳定即可,因此人们可以使用PID调节器进行调节,通过调节合适的[KP]、[TD]、[TI]参数进行闭环控制,从而使智能车以较快速度稳定通过不同的路段。
3.2.2 方向控制。由于舵机具有较大的滞后性,并且智能车在转弯时要求快速响应,因此采用的是PD调节器。利用摄像头采集到的图像计算路径中心与小车中心的偏差值,偏差值通过PD调节器产生的输出控制舵机进行打角,从而控制小车方向。另外,人们可以根据不同的偏差值给定不同的[KP]值和[TD]值,通过试验和测试确定对应的值,使智能车在转弯时快速响应并保持较快的速度。
4 结语
本文以智能小车为载体,对PID控制理论中的公式进行分析,使用MATLAB软件,对不同的PID调节器进行仿真,修改对应的参数,进行横向比较和纵向比较,确定调节器中各个单元的作用和不同调节器的适用范围。最后结合智能车实际行驶中速度控制和方向控制的要求,确定合适的调节器,调节参数,将PID算法在智能车上加以实现,保证了智能车能够高速稳定自动循迹。
参考文献:
[1]肖文健,李永科.基于增量式PID控制算法的智能车设计[J].信息技术,2012(10):125-127.
[2]杨尧.基于MSP430的航空制冷控制专用系统设计与实现[D].成都:电子科技大学,2008.
[3]沈言夫.PID控制在乳化炸药井下装药车上的应用[J].世界有色金属,2018(9):282-283.
[4]胡力刚,许伟明.非线性系统的PID控制器的研究与设计[J].计算机仿真,2010(12):195-199.
