十字芯板钢管阻尼器K型偏心支撑框架的参数分析
2019-09-10胡强陈劲飙
胡强 陈劲飙











摘 要:为研究带十字芯板钢管阻尼器的K型偏心支撑框架结构的抗震性能,采用ABAQUS软件分析了阻尼器的削弱比、厚度比、轴压比等因素对该结构抗震性能的影响,研究了结构的变形性能、破坏形态及耗能能力.结果表明:采用十字芯板钢管阻尼器的K型偏心支撑钢框架结构具有优良的变形能力和耗能性能,结构塑性变形与损伤主要集中于阻尼器,能够有效的保护结构的安全.
关键词:十字芯板钢管阻尼器;偏心支撐;耗能梁段;抗震性能
中图分类号:TU352.1 DOI:10.16375/j.cnki.cn45-1395/t.2019.02.006
0 引言
阻尼器具有优秀的耗能性能,将其用于工程结构,通过阻尼器耗散地震能量,既能有效保护结构主要承重构件,又能方便解决震后修复困难、不易更换等问题[1-5].自1972年Kelly等[6]首次提出金属屈服耗能器以来,钢阻尼器不断发展,先后出现了多种类型的新型金属阻尼器,如:H型钢阻尼器[7]、E型钢阻尼器[8]、X型阻尼器[9]、钢管铅芯阻尼器[10-11]等,并广泛应用于抗风和消能减震结构中.偏心支撑钢框架具有较大的抗侧刚度且延性较好,进入塑性后其抗侧刚度下降缓慢,能够有效保护梁柱等主要构件的安全,因而广泛用于高烈度地震区[12].郭秉山等[13]对K型偏心支撑钢框架支撑的设计方法进行了研究,提出设计和施工建议.冉红东等[14]研究了K型偏心支撑的恢复力模型.近年来众多学者将阻尼器用于偏心支撑结构[15].加拿大学者Mansour等[16]提出了可更换耗能梁段的偏心支撑体系.杨扬等[17]将粘弹性阻尼器代替耗能梁段用于偏心支撑结构,研究了其消能减震原理和单自由度下的地震响应,结果表明,该支撑结构具有良好的抗震性能.孙玉萍等[18]对偏心支撑结构中的粘弹性阻尼器进行了参数优化分析,结果表明,设置消能偏心支撑的结构可以有效地降低结构的地震反应,增加结构自身抵御地震的能力. Moestopo等[19]对普通偏心支撑钢框架与可更换耗能梁段偏心支撑钢框架进行了对比试验.周云等[20-21]将剪切钢板阻尼器和钢管铅芯阻尼器代替耗能梁段用于偏心支撑结构,研究结果表明该结构具有良好的耗能性能.
现有研究表明,阻尼器代替耗能梁段用于偏心支撑结构,成为结构的“保险丝”,地震作用时能够将塑性变形和损伤集中于阻尼器,能大幅降低结构构件的损坏,震后可方便的更换阻尼器,减少结构的维修,降低成本.但现有的阻尼器也存在构造复杂、制作成本高的问题,甚至有的需要较高的密封性要求,难以向需要抗震的普通建筑,尤其是中小城市及乡村建筑推广.十字芯板钢管阻尼器[22]是一种新型金属阻尼器,具有构造简单、制作方便、成本低廉、耗能性能好的特点.因此,本文将该阻尼器代替耗能梁段,通过Abaqus软件建立有限元模型,研究带十字芯板钢管阻尼器的偏心支撑框架结构的抗震性能.
1 带十字芯板钢管阻尼器偏心支撑构造
1.1 十字芯板钢管阻尼器构造及工作原理
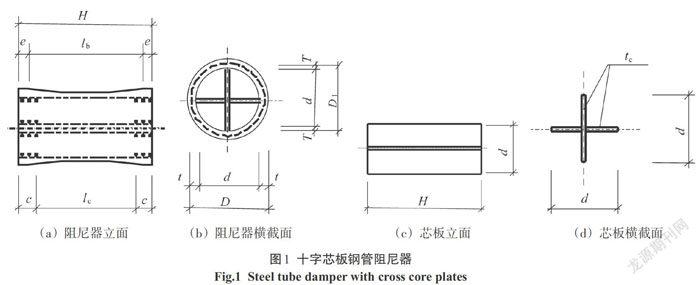
十字芯板钢管阻尼器是由中部削弱的钢管与十字芯板组成,如图1所示.钢管在中部削弱,非削弱段e,厚度t,削弱段lb,最小厚度T;十字芯板为钢板焊接而成,制作时将芯板刨平顶紧套入钢管;两端通过焊缝c将芯板与钢管固定,该焊缝不考虑受力;钢管与端板焊接,形成阻尼器.端板通过螺栓与其他构件连接.该阻尼器具有抗剪承载力高、延性好、耗能性能优秀、结构损伤集中的特点.尤其是构造简单,无密封性要求,制作、安装与更换方便,可大幅降低成本,具有很高的经济价值.
阻尼器通过钢管与十字芯板的塑性变形耗能.荷载作用时,钢管与十字芯板相互约束、协同工作,大幅提高了阻尼器的钢板件的屈曲临界荷载,使得阻尼器能产生大量的塑性变形消耗地震能量.当结构遭受低于设防地震等级的地震作用时,结构与阻尼器均为弹性;当遭受设防等级或大于设防等级的地震作用时,结构其他部位或构件基本处于弹性阶段,无损伤或损伤很小,塑性变形和损伤集中于阻尼器,通过阻尼器的塑性变形消耗地震能量,直至阻尼器失效;震后可方便更换阻尼器,结构仍可继续使用.
为了研究阻尼器对K形偏心支撑力学性能的影响,设计阻尼器D0[22],并以此为基础,改变钢管削弱厚度与芯板厚度,得到表1所示共5个阻尼器.
1.2 偏心支撑构造
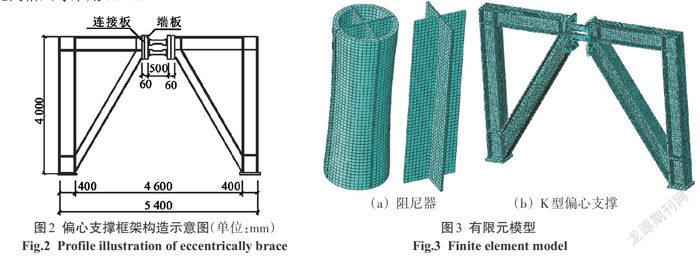
试件模型参照文献[21]所示K型偏心支撑框架,如图2所示,跨度5 m,高4 m;耗能梁段0.5 m,为两个阻尼器;非耗能梁段构件即梁柱与支撑均采用400 mm×400 mm×24 mm×16 mm工字型截面;连接板与端板采用870 mm×500 mm×30 mm钢板.钢材采用双线性随动强化模型,弹性模量Es=206 000 MPa,泊松比v=0.3,屈服后弹性模量És=2%Es.阻尼器钢材屈服强度235 MPa,极限应力375 MPa;框架梁柱及支撑等非耗能部分屈服强度360 MPa,极限应力560 MPa.采用6个10.9级M24摩擦型高强螺栓,屈服强度650 MPa,极限应力800 MPa,线膨胀系数0.000 012,螺栓预紧力225 kN,有限元模型中采用降温法施加预紧力.
2 模型的建立
采用ABAQUS软件建立带十字芯板钢管阻尼器的偏心支撑框架有限元模型,如图3所示.其中梁、柱、斜撑、底板、梁端板之间,阻尼器钢管、芯板、阻尼器端板之间均采用绑定连接;梁端板与阻尼器端板间采用接触连接,法向为硬接触,切向为摩擦系数为0.45的罚函数;螺栓的螺杆、螺帽、螺母通过Merge合并为单个部件,螺帽、螺母与端板接触面采用绑定连接,螺杆为端板螺栓孔接触面采用硬接触.所有构件均采用C3D8R单元.经多次试算,当梁与阻尼器端板厚度不小于30 mm时,端板的弯曲变形已很小,可忽略不计;同时,当阻尼器、端板及连接板单元网格尺寸不大于0.01 m,梁、柱及支撑的单元网格尺寸不大于0.05 m时,计算结果的差别已经很小,故而取上述值为有限元模型的网格尺寸.另外,底板单元网格尺寸采用0.1 m.
加载方式为低周反复加载,位移加载,参照文献[20-21]采用最大加载位移30 mm.低周反复加载每等级5 mm,每等级循环一次.考虑轴压比影响时,在左右两柱柱顶施加相应轴向力.底板与参考点耦合,并约束参考点所有自由度.
3 结果分析
3.1 力学性能
对应表1所示阻尼器,在阻尼器编号前冠以K表示帶十字芯板钢管阻尼器的K型偏心支撑试件.对各试件进行反复加载,试件的初始刚度、屈服后刚度、屈服荷载、屈服位移、最大加载位移时的荷载(极限荷载)及前5次循环的等效粘滞阻尼系数如表2所示.总的来说,采用十字芯板钢管阻尼器的K型偏心支撑框架结构具有较高的初始刚度和较大的承载力;其等效粘滞阻尼系数从第二循环开始均能达到0.2以上,从第三循环开始均能达到0.28以上,表明该结构具有良好的耗能性能.
3.2 应力、应变分布
3.2.1 Mises应力分布规律
以试件K-D0为例对最大加载位移及加载过程中应力及塑性应变进行分析.最大加载位移时,框架及阻尼器的Mises应力分布如图4所示.框架应力主要集中于柱脚腹板钢材,最大应力为390 MPa,表明刚进入屈服,而其他位置的应力均远小于框架钢材的屈服应力360 MPa,因此需适当加强柱脚腹板.钢管的Mises应力峰值主要集中在两端削弱处上下表面A区域及中部两侧面B区域,最大应力为358 MPa,已超出其屈服应力235 MPa约52%;芯板的Mises应力峰值主要集中于削弱处对应的竖板两端C区域及中部D区域,最大应力为358 MPa,已超出其屈服应力235 MPa约52%.
3.2.2 塑性应变分布规律
框架的塑性应变表现为剪应变PE12较大,位于柱脚腹板,其峰值为0.007 8;正应变PE22最大值也位于柱脚腹板,其峰值为0.001 8;其应变值远小于阻尼器的应变,故文中未示出.
阻尼器塑性应变如图5所示.钢管与芯板正应变PE11分别集中于A及C区域,峰值应变分别为0.037及0.032;钢管与芯板剪应变PE12分别集中于B及D区域,峰值应变分别为0.061及0.055.
阻尼器各循环塑性应变峰值随加载位移的变化曲线如图6所示.屈服后,塑性剪应变大于塑性正应变、钢管塑性应变大于芯板塑性应变.表明钢管是主要的耗能部件,阻尼器主要通过剪切变形耗能.
3.2.3 耗能模式
上述分析表明结构的塑性变形集中于阻尼器,阻尼器起到了耗能作用,有效地保护了结构.因此,带十字芯板钢管阻尼器K型偏心支撑框架的耗能模式为:荷载作用下试件的塑性变形集中于阻尼器,框架基本处于弹性状态;阻尼器通过中部剪切变形与端部拉压变形混合耗能,且以剪切变形为主.
3.3 削弱比的影响
3.3.1 承载力及耗能性能
以K-D0为基础,改变钢管中部管壁厚度T,削弱比T/t即削弱后壁厚T与削弱前壁厚t之比分别为0.67与0.40,得到试件K-DTt6与K-DTt4.三个试件的骨架曲线如图7所示,随着削弱程度的增大,试件刚度及承载力逐渐降低.
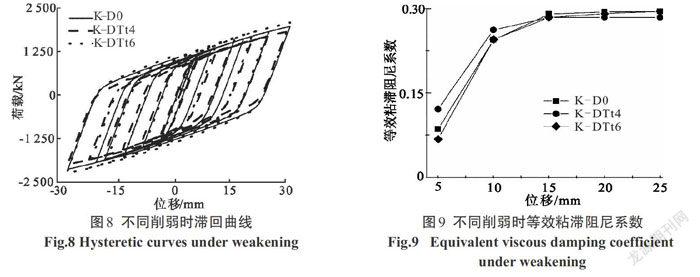
三个试件的滞回曲线与等效粘滞阻尼系数如图8与图9所示.滞回曲线均较为饱满;削弱大的试件 K-DTt4前两次循环的等效粘滞阻尼系数略大,后期循环却较小;到第五循环时试件K-D0及K-DTt6的等效粘滞阻尼系数曲线趋于一致.表明钢管削弱过大时会导致试件后期循环的耗能能力降低.
3.3.2 峰值Mises应力及峰值塑性应变
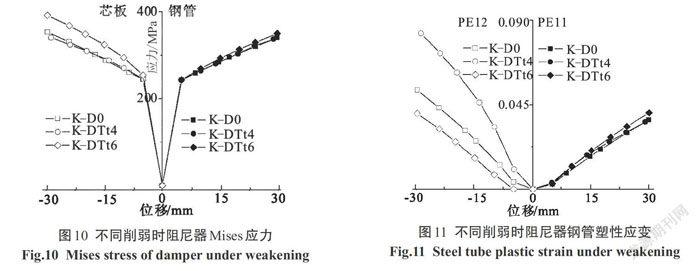
如图10所示为不同削弱比时各循环A区域和C区域Mises峰值应力随位移变化.削弱程度对钢管Mises应力影响不大;随着削弱程度的增大,芯板Mises应力随之减小,当削弱增大到一定程度时,Mises应力不再继续减小.
如图11所示,各循环峰值应变随着削弱增大,钢管A区塑性正应变变化不大,但B区塑性剪应变急剧增大,甚至达到A区塑性正应变的2倍.
图12所示为各循环芯板塑性应变峰值变化规律,随着削弱增加,芯板C区域正应变减小,削弱比小于某值时趋于稳定;但芯板D区塑性剪应变急剧增大.
表明增大削弱可显著增加钢管和芯板中部的塑性剪应变,达到通过剪切变形耗能的目的;但削弱过大将导致后期耗能能力降低.
3.4 厚度比的影响
3.4.1 承载力及耗能性能
仍以K-D0为基础,改变芯板厚度tc,厚度比tc/t分别为0.67与0.20,得到试件K-Dtct6与K-Dtct2.三个试件的骨架曲线如图13所示,随着芯板厚度增加,试件的承载力随之增大.
三个试件的滞回曲线与等效粘滞阻尼系数曲线如图14与图15所示.滞回曲线均较为饱满.芯板厚度很大时,芯板塑性变形发生较晚,不能及时参与耗能,导致试件前期耗能能力较弱;芯板厚度较小时,耗能能力也较大;到第五循环时,三个试件的等效粘滞阻尼系数趋于一致,但芯板厚度最小的试件K-Dtct2的等效粘滞阻尼系数有降低的趋势.
3.4.2 峰值Mises应力及峰值塑性应变
图16为各循环A与C区域Mises应力峰值随芯板厚度的变化曲线,表明改变芯板厚度对阻尼器应力影响不显著.
图17为各循环钢管A与B区域塑性应变随芯板厚度的变化.显然,钢管塑性正应变的变化不明显,而钢管中部塑性剪应变随芯板厚度减小明显增大.
图18为各循环芯板C与D区域塑性应变随芯板厚度的变化.芯板端部即C区域塑性正应变随芯板厚度减小而减小,中部即D区域塑性剪应变却显著增大.
上述结果表明芯板厚度减小能显著增大阻尼器中部塑性剪应变,有利于阻尼器通过剪切变形耗能;但过小的芯板厚度将降低后期耗能性能.
3.5 轴压比的影响
3.5.1 承载力及耗能性能
不同轴压时试件的骨架曲线如图19所示.当轴压较小即轴压力小于3 000 kN时,承载力几乎没有变化;当轴压较大时,试件承载力随之减小;当轴压力接近甚至大于柱的稳定承载力时(按框架柱算得柱面内稳定承载力约为8 900 kN),如表2所示,试件极限承载力减小了约12%.
试件的滞回曲线如图20所示,当轴压力小于柱稳定承载力时,试件滞回曲线均较为饱满;当轴压大于稳定承载力时,滞回曲线反而变得更加方正,耗能能力增强.
试件的等效粘滞阻尼系数曲线如图21所示.试件的耗能能力随轴压增大而增大;当轴压过大时,试件耗能能力反而很大.
3.5.2 峰值Mises应力及峰值塑性应变
由图22—图25所示各循环Mises应力及塑性应变峰值的变化曲线可知:当轴压不超过柱稳定承载力时,轴压对阻尼器Mises应力影响不显著;轴压增大将使阻尼器塑性正应变减小,而对塑性剪应变的影响不大;轴压增大将使柱脚腹板塑性应变显著增大.
究其原因,是由于轴压导致结构构件产生一定的变形和应力;水平荷载作用时应力随之增大并使构件局部进入塑性,使得结构不同程度的参与耗能,故其耗能能力提高;但也使得结构构件产生较大的塑性变形和损伤,导致阻尼器的耗能作用降低.因此,需限制试件的轴压不超过6 000 kN,即轴压比不大于0.67.
4 结论
1)阻尼器的耗能模式为中部剪切变形与端部拉压变形混合耗能,且以剪切变形耗能为主.设计合适的阻尼器,选取合适的板件尺寸和削弱程度,能够充分发挥阻尼器的耗能作用,并保证K型偏心支撑框架结构具有良好的力学性能和优良的耗能能力.
2)随着钢管削弱的增大,阻尼器的塑性应变增大,结构的塑性变形和损伤越集中于阻尼器.但过大的削弱(削弱比T/t<0.4)将使结构后期耗能性能降低.
3)随着芯板厚度的减小,阻尼器的塑性应变增大,结构的塑性变形和损伤越集中于阻尼器.但过小的芯板厚度(厚度比tc/t<0.4)将使结构后期耗能性能降低.
4)柱轴压使构件产生一定的变形和应力,导致水平荷载作用时部分构件也进入塑性参与耗能,使构件产生一定的损伤;同时阻尼器的塑性应变有所减小.因此,应严格柱轴压比(轴压比不大于0.67),以减小结构的损伤,充分发挥阻尼器的耗能性能和对结构的保护作用.
参考文献
[1] 吕西林,陈云,蒋欢军. 新型可更换连梁研究进展[J]. 地震工程与工程振动,2013,33(1):8-15.
[2] 欧进萍,吴斌. 组合钢板屈服耗能器性能及对其高层钢结构减振效果的试验研究[J]. 建筑结构学报,2001,22(1):26-32.
[3] 张敏,汪东卓. 摩擦阻尼器在框架结构平面中合理布置分析[J]. 广西科技大学学报,2018,29(3):15-23.
[4] 沈星,倪晓博,叶爱君. 大跨度斜拉桥边墩新型横向钢阻尼器减震体系及设计方法[J]. 土木工程学报,2016,49(5):110-119.
[5] 张敏,占科彪. 底部框架双功能减震结构地震响应分析[J]. 广西科技大学学报,2017,28(3):38-46.
[6] KELLY J M,SKINNER R I,HEINE A J. Mechanisms of energy absorption in special devices for use in earthquake resistant structures[J]. Bulletin of New Zealand Society for Earthquake Engineering,1972,5(3):63-68.
[7] 王爽. 新型开孔H型钢阻尼器参数分析与抗震性能研究[D]. 广州:广州大学,2012.
[8] 潘晋,吴成亮,仝强,等. E型钢阻尼器数值仿真及试验研究[J]. 振动与冲击,2009,28(7):192-195.
[9] WHITTAKER A ,BERTERO V V,THOMPSON C L,et al. Seismic testing of steel plate energy dissipation devices[J]. Earthquake Spectra, 1991,7(4):563-604.
[10] 盧德辉,周云,邓雪松. 钢管铅芯阻尼器性能分析研究[J]. 地震工程与工程振动,2013,33(6):215-221.
[11] 周云,卢德辉,张敏. 钢管铅阻尼器的性能试验研究[J]. 土木工程学报,2017,50(1):46-52.
[12] 胡含笑. 偏心支撐钢框架高层建筑的抗震性能分析[D]. 昆明:昆明理工大学,2017.
[13] 郭秉山,庄晓勇,闫月梅. K型偏心支撑钢框架支撑的设计研究[J]. 西安科技大学学报,2007,27(1):30-34.
[14] 冉红东,郝麒麟,苏明周. 高强组合钢K型偏心支撑框架恢复力模型[J]. 西安建筑科技大学学报(自然科学版),2013,45(5):627-632.
[15] 蔡益燕,钱稼茹,郁银泉. 偏心支撑框架设计新进展[J]. 建筑结构,2011,41(4):7-10.
[16] MANSOUR N,SHEN Y L,CHRISTOPOULOS C,et al. Experimental evaluation of nonlinear replaceable links in eccentrically frames and moment resisting frame[C]. 14WCEE, LISBOA,2008.
[17] 杨扬,郝际平,卢坤林,等. 设置粘弹性阻尼器的偏心支撑结构性能研究[J]. 工业建筑, 2007,37(S1):287-291.
[18] 孙玉萍,吴磊,何晴光,等. 消能偏心支撑结构中粘弹性阻尼器的参数优化[J]. 工程抗震与加固改造,2009,31(1):48-51.
[19] MOESTOPO M,NOVAN A,MIRZA A,et al. On improved performance of eccentrically braced frames with replaceable shear link[C]. 15WCEE,Lisboa,2012.
[20] 周云,何志明,张超,等. 可更换剪切钢板阻尼器偏心支撑框架分析[J]. 地震工程与工程振动, 2015, 35(5):68-78.
[21] 何志明,周云,卢德辉,等. 可更换钢管铅芯阻尼器偏心支撑框架分析[J]. 工程抗震与加固改造,2016,38(1):79-88.
[22] 胡强,贾松林,王丹,等. 十字芯板钢管阻尼器力学性能研究[J]. 四川建筑科学研究,2017,43(6):66-71.
Parameter analysis of K-type eccentric brace with cross core
plates steel tube damper
HU Qiang, CHEN Jinbiao
(School of Civil Engineering and Architecture, Guangxi University of Science and Technology,
Liuzhou 545006, China)
Abstract: To study seismic performance of K-type eccentric brace with cross core plates steel tube damper, finite element models were built by ABAQUS software to analyze influences of different weakening in steel tube, thickness of the core plates, and axial compression on deformability, failure mode and energy dissipation. The results show that K-type eccentric brace with the proposed damper is advantageous in deformability and energy-dissipation behavior, plastic deformation and damage are concentrated on the damper to ensure the safety of the structure.
Key words: steel tube damper with cross core plates; eccentric brace; energy-dissipated link; seismic behavior
