基于R-FPOP变点检测的城市路段旅行时间预测

商明菊 胡尧 周江娥 王丹

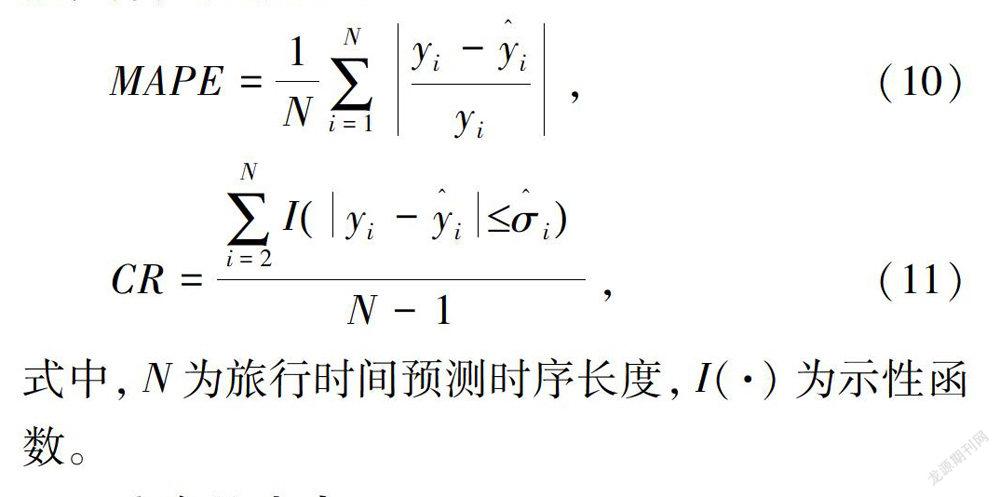
摘 要：针对城市路段旅行时间精准推送的不足，提出一种基于动态规划变点检测算法的旅行时间预测方法。以车牌识别数据为研究对象，利用R-FPOP算法对旅行时间均值变点进行在线检测，研究变点时域分布特征;基于均值变点检测结果，预测旅行时间并给出其预测区间。结果表明：在线检测出的变点能够有效辨识旅行时间的均值突变，变点时域分布主要集中在高峰期;旅行时间预测值对实际序列变化趋势估计准确，推送的预测区间平均覆盖率为79.54%，具有较优的预测精度。论文方法兼顾旅行时间均值突变且建模简单，可为路段旅行时间的在线智能推送及交通需求者的路线规划提供技术支持。

关键词：交通工程;旅行时间预测;R-FPOP;变点;智能导航

中图分类号：U491.1

文献标识码： A

旅行时间预测是交通出行者的重要需求，也是路网均衡诱导的关键。随着城市卡口监控系统不断升级，利用车牌识别数据快速、有效推送路段旅行时间，成为交通领域研究的热点。车牌识别数据作为针对城市道路行驶车辆的实时监测数据，具有持续生成且数据量大、时空相关等特性[1]。交通拥堵的本质是交通需求失衡，旅行时间能直观反映从起点到终点的出行成本，是表征路段交通拥堵状态的一个直观、有效的交通流参数。在城市主次干道系统中，随着拥堵程度的增加，由于信号控制的存在，車辆将以一定的饱和流率放行，路段旅行时间不会无限增长，而是趋于一个稳定的较高值。为利用车牌识别数据高效、准确计算旅行时间，赵卓峰等[1]给出旅行时间计算定义，并提出一种基于时空划分的流水线式并行计算模型。数据爆发式增长趋势下，数据流实时、连续、无监督异常检测方法[2]被提出;自动编码器[3]、递归神经网络[4]、递归最小二乘滤波[5]等模型，被应用于交通流参数预测。然而，柴华骏等[6]对道路交叉口车牌识别数据进行分析时，发现道路拥堵时旅行时间接近Weibull分布，通畅时接近对数正态分布，使用正态分布估计旅行时间均值误差较小。这一现象与旅行时间非平稳、随机突变特点有关，也使得常规统计预测模型建模受阻。

交通流变点是交通流模型中某个或某些参数突变之点[7]，近年来被逐渐应用到交通管理中，如速度预测[8]、道路交叉口事故监测[9]、拥堵状态自动识别[10]、交通流突变概率估计[11]、交通法规干预效果评价[12]等。变点发生后，交通流参数将发生质的变化。小粒度的收集交通流数据，可以快速检测正在突变的交通流变化，利于路况信息的及时发布。结合多源交通流数据，在线Bayesian变点检测方法被应用到个体出行模式突变概率估计[13]和交通拥堵概率估计[14]。然而，变点检测的关键在于算法的检测延迟、稳健性、变点源剖析以及无监督方法，通常非参数方法比参数方法稳健[15]。同时，采集到的实际数据常由于设备故障、交通事件突发等原因，非平稳且存在缺失或异常。交通流变点检测的难点就在于在线快速区分真实突变与异常值，这是大多数现有变点检测方法难以做到的，如WU等[16]提出的使用粒子滤波技术的变点检测方法，其参数易于选择，但其高稳健性和检测精度却以较高的计算成本为代价。因此，利用对异常值不敏感的变点检测方法，在线检测路段旅行时间变点并研究其在线推送问题，具有重要意义。

一种常用的方法是引入分割成本，如将负对数似然、平方损失等函数作为数据分割的成本，进而通过最小化该分割成本函数来检测变点。解决此类最小化问题，通常采用动态规划算法求解。变点个数已知时，为约束最小化问题，RIGAILL[17]就此提出基于函数修剪的pDPA（pruned Dynamic Programming Algorithm）来解决。然而，实际问题中变点个数往往是未知的。为此，JACKSON等[18]引入惩罚项，将变点检测转化为成本函数惩罚最小化问题，提出OP （Optimal Partitioning）算法;它的计算复杂度优于SNS（Segment Neighborhood Search）[19]，但在数据量较大的情况下，计算依旧复杂。随后，KILLICK等[20]提出基于不等式修剪的PELT（Pruned Exact Linear Time）算法，它比OP更有效且计算简单。这些方法均可描述为三个要素的集合，即成本函数、搜索方法和对变点个数的约束[21]。2017年，MAIDSTONE等[22]结合PELT与pDPA，提出使用函数修剪最优分割（Functional Pruning Optimal Partitioning，FPOP）算法来解决惩罚最小化问题，与现有的动态规划算法相比，其计算效率更高、检测性能更稳健。同年，为解决异常值存在情况下实测数据的在线变点检测问题，FEARNHEAD等[23]提出稳健的函数修剪最优分割（Robust Functional Pruning Optimal Partitioning，R-FPOP）算法，它利用对异常值不敏感的有界损失函数在线稳健检测变点，计算简便且准确率高。

鉴于此，本文针对车牌识别数据集上路段旅行时间精准推送的需求，利用稳健、高效的R-FPOP算法，解决路段旅行时间均值变点的在线检测问题，对变点时域分布进行研究，预测旅行时间并在线推送其预测区间，为交通需求者出行路线的规划提供参考。

2 路段旅行时间预测方法

在车辆行驶轨迹途径路段各交叉口的前提下，路段起止卡口系统先后采集到同一车辆的采集时间差即为车辆旅行时间。它为车辆行经路段的实际花费成本，其值越小，表明交通运行状态越好，路段越通畅;反之，越拥堵。

由于车牌识别错误、漏检等系统误差的存在，原始数据存在噪声;同时，在某些情况下，如偶然停车、中途离开等真实数据偏差的存在，使得车辆旅行时间不能反映整个交通流实际运行状态。因此，为屏蔽不合理车辆旅行时间带来的影响，当车辆经过起止卡口的时差小于某一临界值D时，才采集该车旅行时间。考虑到短时在线推送的必要性及数据采集的可靠性，当检测到的车辆数不低于2时，直接采用中位数法[1]获取路段旅行时间;若某时段检测到的车辆数低于2，不对该时段观测值进行填补，变点检测时不计分割成本即可。实际数据处理时，由于公交车行经站台需停车上下客，故将其剔除。虽然出租车也存在停车待客现象，但考虑到它作为交通需求者便捷出行的首选，对交通运行状态的评估起着关键作用，将其保留。

旅行时间预测值y^t，采用时刻t-1前变点集中距离最近的变点τm后第一个观测点到时刻t-1时的子数据集yτm+1：t-1经异常处理后的均值来估计。预测区间长度过大是无意义的，基于Sigma原则，定义预测区间[y^t-σ^t，y^t+σ^t]。采用异常处理后子数据集yτm+1：t-1的标准差作为σ^t的估计。需要特别说明的是，子数据集yτm+1：t-1经异常处理后：若为空，y^t用y^t-1估计;若时序长度小于2，σ^t用σ^t-1估计。采用预测误差百分比绝对值均值（Mean Absolute Percentage Error，MAPE）与预测区间覆盖率（Coverage Ratio，CR）来评价预测方法性能，计算公式如下：

3 实例测试

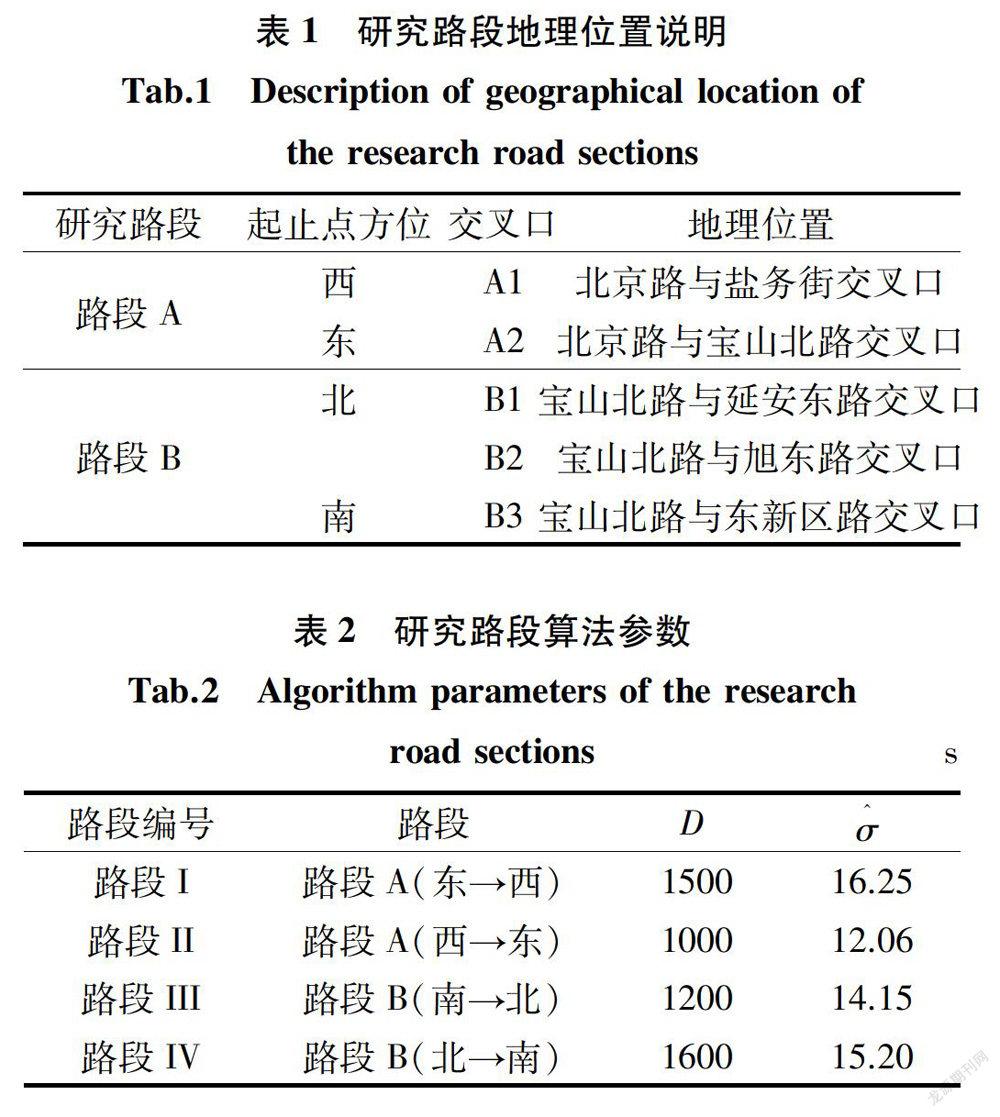
选取贵阳市一环宝山北路、北京路沿线的路段为研究对象，以2017年7月车牌识别数据为例，对旅行时间时序进行均值变点检测，各路段地理位置说明见表1。为估计变点检测算法参数，取1日至23日车辆日记录缺失比不高于10%的数据作为训练集;同时，取24日至30日的数据作为测试集，用于检验预测方法的有效性。调取车辆卡口监测信息，对行驶路线与路段卡口方位匹配的车辆，在剔除不符合起止卡口监测点时差临界值D的观测值后，計录车辆旅行时间，最后采用中位数法得到路段旅行时间（单位：s）。为确保快速推送，采集粒度取2 min，每天共720个观测值。检测时段采用时间点标记，如时段[00：00-00：02）记为“00：00”。在训练集上通过模糊聚类与中位数法，确定各路段旅行时间临界值D与噪声标准差σ^，结果见表2。

3.1 路段旅行时间均值变点

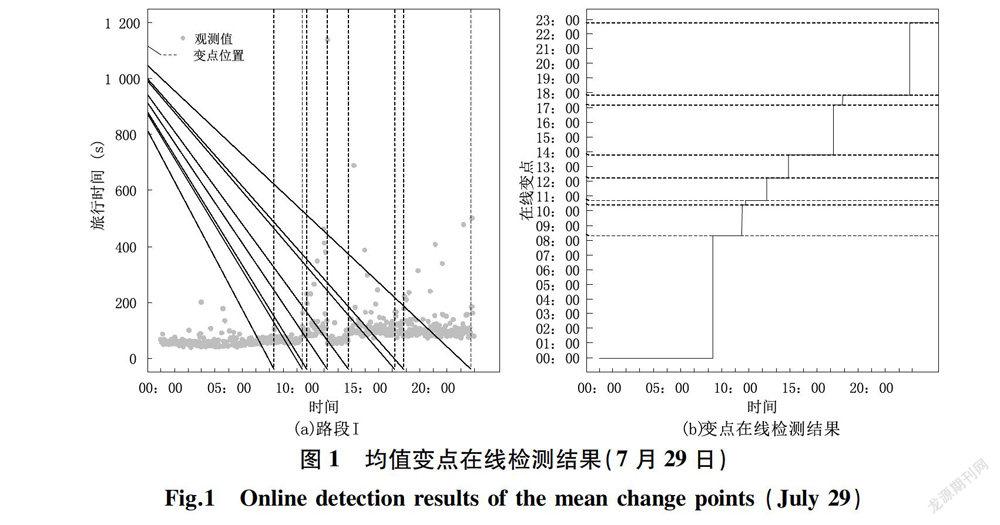
采用R-FPOP算法对测试集各路段旅行时间时序进行在线均值变点检测。以7月29日路段I为例，除时序起止点外，共在线检测出8个变点，区段示意见图1（a）。从图1（a）中可以发现，在交通需求的随机扰动下，路段旅行时间均值跳跃现象明显，呈现出由一种稳定态突变到另一种稳定态的随机现象。由图1（b）可知，在异常值干扰的情况下，在线变点仍然能被快速检测，最短检测延迟时间为2 s。

利用动态规划思想，由在线变点检测结果递推得到全天时序的最优分割，即离线变点，结果如图2所示。由图2可知，各路段离线均值变点时域上分布不均匀，如 [10：00-12：00）两小时内，路段IV共检测出9个变点，而路段I只检测出1个变点。这也反映了旅行时间集群性与均值变点随机性特点。以路段IV为例，离线变点τ3（09：36）、τ4（10：22）、τ5（10：32）、τ6（10：36） 划分得到区段yτ3+1：τ4、yτ4+1：τ5、yτ5+1：τ6的旅行时间均值分别为139.83 （s）、391.17 （s）、651.00 （s），τ4、τ5处跳跃度分别为251.34 （s）、259.83 （s）。可以发现，各区段旅行时间徒升、跳跃幅度大，[10：24-10：34）行经路段IV的出行成本为[09：38-10：24）的2.80倍。若“10：24”检测到旅行时间突变同时发布诱导信息，有助于出行者及时规划调整行车路线。从图2也可发现，受贵阳市一环商业经济圈交通需求的影响，高峰时段旅行时间跳跃现象频繁且跳跃度波动较大。采用非参数Wilcoxon秩检验，评估离线变点是否将相邻时序长度均大于15的实际序列准确划分。显著性水平0.01下，相邻区段均值检验p值均显著，这实证了R-FPOP算法检测的均值变点有效且检测性能优。

进一步分析车辆日记录缺失比不低于10%的全数据集上在线检测的旅行时间均值变点特征。在频率分布基础上，利用核密度法估计均值变点时域分布的密度曲线，结果见图3。从图3可以看出，各研究路段旅行时间均值变点时域分布有较大差异，路段I、IV变点主要集中在早高峰，而路段II、III变点在晚高峰出现的概率略高于早高峰，这与路段双向各时段的交通需求密切相关。路段A是相邻片区大部分车辆由东向西进入贵阳市一环的首选，路段B紧邻集医疗、教育、金融为一体的繁华经济生活圈，这两条路段早高峰的交通发生量相对较大。若向出行者及时发布旅行时间历史均值及其突变概率，可在一定程度上合理引导其规划最优路线，进而均衡路网交通需求。

3.2 路段旅行时间预测

利用在线均值变点实时划分区段的子数据集来预测各路段旅行时间，计算预测值的MAPE与预测区间覆盖率指标来衡量预测精度，结果分别见图4、表3、表4。对旅行时间在线推送方法进行说明：以7月29日路段II为例，假设当前时刻“10：16”，检出的最近变点为“09：56”，于是将时段[09：58-10：16）内异常处理后观测值的均值144.11（s）记为y^10：16，同时估计出σ^10：16为10.71（s），进一步得到预测区间[133.40，154.82]，真实值150.00（s）被预测区间准确覆盖，预测误差百分比绝对值为393%。

从图4可以看出，各路段旅行时间时序虽波动较大，但预测时序与真实时序整体走势相契合。由表3可知，测试集上路段I-IV旅行时间平均MAPE分别为13.47%、11.53%、10.01%、9.88%，整体平均MAPE为11.22%，这说明时序的变化趋势得到了较好预测。由表4可知，测试集上路段I-IV平均覆盖率分别为81.67%、78.31%、79.23%、78.94%，整体平均覆盖率为79.54%，预测精度较高，这说明提出的预测方法具有一定的实时性与有效性。由此，可为导航系统智能推送路段旅行时间预测值及其预测区间，将路段出行成本量化，从而诱导交通需求者择优出行，进而缓解交通拥堵，提高城市道路使用率。

综上，结合路段旅行时间的均值突变信息对旅行时间进行预测，得到了较准确的预测结果，方法的突出优点在于它建模简单、可操作性强，能够满足在线智能推送的需要。实际应用时，若实时数据长时段缺失，可与历史数据进行时空模式匹配来进行预测。

4 结论

（1）在实时获取车牌识别数据的情况下，本文利用稳健的变点检测算法对路段旅行时间均值变点进行在线检测，将其结果用于预测旅行时间。研究发现R-FPOP算法可以较好的辨识旅行时间均值突变且检测延迟小，均值变点具有随机性且高峰期内出现的概率较大;推送的旅行时间平均MAPE为11.22%、预测区间平均覆盖率为79.54%，预测效果优良。

（2）本文方法建模简单且操作性强，对于导航系统路段旅行时间的精准推送以及交通信息服务等具有一定的支撑作用。为保证卡口数据采集质量，研究路段较短，进一步需结合信号灯的影响以及多元时间序列在线变点检测方法，探究出行路线旅行时间的预测。

参考文献：

[1]赵卓峰，丁维龙，张帅. 海量车牌识别数据集上基于时空划分的旅行时间计算方法[J].电子学报，2016，44（5）：1227-1233.

[2]AHMAD S， LAVIN A， PURDY S， et al. Unsupervised real-time anomaly detection for streaming data[J]. Neurocomputing， 2017，262：134-147.

[3]LV Y， DUAN Y， KANG W， et al. Traffic flow prediction with big data： a deep learning approach[J]. IEEE Transactions on Intelligent Transportation Systems， 2015，16（2）：865-873.

[4]GUO T， XU Z， YAO X， et al. Robust online time series prediction with recurrent neural networks[C]//International Conference on Data Science and Advanced Analytics. Montreal， Canada： IEEE， 2016：816-825.

[5]COMERT G， BEZUGLOV A， CETIN M. Adaptive traffic parameter prediction： effect of number of states and transferability of models[J]. Transportation Research Part C： Emerging Technologies， 2016，72（11）：202-224.

[6]柴華骏，李瑞敏，郭敏. 基于车牌识别数据的城市道路旅行时间分布规律及估计方法研究[J].交通运输系统工程与信息，2012，12（6）：41-47.

[7]王晓原，隽志才，贾洪飞，等. 交通流突变分析的变点统计方法研究[J].中国公路学报，2002，15（4）：69-74.

[8]JEON S， HONG B. Monte Carlo simulation-based traffic speed forecasting using historical big data[J]. Future Generation Computer Systems， 2016， 65： 182-195.

[9]SUREGAONKAR S， ASHOK S D， KARAR V， et al. Change point monitoring for vehicle incident detection at intersection[C]//International Conference on Science Technology Engineering and Management. Chennai， India： IEEE， 2017：100-105.

[10]YAN Q， SUN Z， GAN Q， et al. Automatic identification of near-stationary traffic states based on the PELT changepoint detection[J]. Transportation Research Part B： Methodological， 2018， 108（2）：39-54.

[11]ARNESEN P， HJELKREM O A. An estimator for traffic breakdown probability based on classification of transitional breakdown events[J]. Transportation Science，2017， 52（3）：593-602.

[12]SHENG R， ZHONG S， BARNETT A G， et al. Effect of traffic legislation on road traffic deaths in Ningbo， China[J]. Annals of Epidemiology，2018， 28（8）：576-581.

[13]ZHAO Z， KOUTSOPOULOS H N， ZHAO J. Detecting pattern changes in individual travel behavior： a Bayesian approach[J]. Transportation Research Part B： Methodological， 2018，112（06）：73-88.

[14]KIDANDO E， MOSES R， SANDO T， et al. Evaluating recurring traffic congestion using change point regression and random variation Markov structured model[J]. Transportation Research Record， 2018， 2672（20）：63-74.

[15]AMINIKHANGHAHI S， COOK D J. A survey of methods for time series change point detection[J]. Knowledge and Information Systems， 2017， 51（2）：339-367.

[16]WU J， CHEN Y， ZHOU S， et al. Online steady-state detection for process control using multiple change-point models and particle filters[J]. IEEE Transactions on Automation Science and Engineering， 2016， 13（2）：688-700.

[17]RIGAILL G. A pruned dynamic programming algorithm to recover the best segmentations with 1 to Kmax change-points[J]. Journal de la Société Francaise de Statistique， 2015， 156（4）：180-205.

[18]JACKSON B， SCARGLE J D， BARNES D， et al. An algorithm for optimal partitioning of data on an interval[J]. IEEE Signal Processing Letters， 2005， 12（2）：105-108.

[19]AUGER I E， LAWRENCE C E. Algorithms for the optimal identification of segment neighborhoods[J]. Bulletin of Mathematical Biology， 1989， 51（1）：39-54.

[20]KILLICK R， FEARNHEAD P， ECKLEY I A. Optimal detection of changepoints with a linear computational cost[J]. Journal of the American Statistical Association， 2012， 107（500）：1590-1598.

[21]TRUONG C， OUDRE L， VAYATIS N. Selective review of offline change point detection methods. ArXiv e-print，2019，1801.00718v2.

[22]MAIDSTONE R， HOCKING T， RIGAILL G， et al. On optimal multiple changepoint algorithms for large data[J]. Statistics and Computing， 2017， 27（2）：519-533.

[23]FEARNHEAD P， RIGAILL G. Changepoint detection in the presence of outliers[J]. Journal of the American Statistical Association， DOI：10.1080/01621459.2017.1385466.

[24]HAYNES K， ECKLEY I A， FEARNHEAD P. Computationally efficient changepoint detection for a range of penalties[J]. Journal of Computational and Graphical Statistics，2017， 26（1）：134-143.

[25]YAO Y C， AU S T. Least-squares estimation of a step function[J]. Sankhyā：The Indian Journal of Statistics， Series A，1989，51（3）：370-381.

[26]HUBER P J. Robust statistics[M]//LOVRIC M. International Encyclopedia of Statistical Science. Berlin， Heidelberg： Springer， 2011：1248-1251.

[27]FRYZLEWICZ P. Wild binary segmentation for multiple change-point detection[J]. The Annals of Statistics，2014， 42（6）：2243-2281.

（責任编辑：于慧梅）