决策树分析法在工程项目工期优化中的应用

摘  要：工程项目网络进度计划的实施过程中，对网络计划进行工期优化是非常普遍的，最常见的情况是对剩余工作进行工期压缩，以保证项目能够按时竣工。在网络计划的工期压缩决策时，常用选择工作压缩单位时间成本最少的方法与工程实施的现实相比有几个弊端。本文结合项目实例，建立工期压缩时的单位时间成本增加值与时间的函数关系，更贴近实际成本。引入决策树分析法计算风险对工期目标实现的影响，从而为工期压缩的决策提供依据。

关键词：双代号网络计划;工期优化;决策树

中图分类号：TP311.13      文献标识码：A 文章编号：2096-4706（2019）23-0098-03

The Application of Decision Tree Analysis in the Optimization of Construction Period

CHEN Xu

（Beijing Huadian Tianren Power Control Technology Co.，Ltd.，Beijing  100039，China）

Abstract：In the process of the implementation of network schedule，it is very common to optimize the network schedule，the most common situation is to compress the remaining work to ensure the project can be completed on time. In the decision-making of time compression of network planning，there are several disadvantages in the method of choosing the least unit time cost of work compression compared with the reality of project implementation. This paper establishes the functional relationship between the added value of unit time cost and time during time compression，which is closer to the actual cost. The decision tree analysis method is introduced to calculate the impact of risk on the realization of construction period goal，so as to provide a basis for the decision-making of construction period compression.

Keywords：double code network plan;duration optimization;decision tree

0  引  言

工程進度网络计划技术是项目进度管理的有效手段，它符合工程施工的要求，特别适用于施工的组织和管理，已经在我国的工程施工单位中得到了比较广泛的应用。但在网络计划技术应用后的管理上还比较薄弱，特别是进度计划执行中的跟踪调整方面还有待改进。

1  进度计划调整优化的必要性

工程项目在实施过程中，由于组织、管理、经济、技术、资源、环境和自然条件等因素的影响，往往会造成实际进度与计划进度产生偏差的情况，如果偏差不能及时纠正，必然影响到最终进度目标的实现[1]。

2  工程项目进度计划调整的内容和方法

项目进度计划的调整，以压缩工期最为常见。在进行压缩工期计划时，通常含有以下的内容[2]：（1）调整关键线路的长度;（2）调整非关键工作的工作时差;（3）增加或减少工作项目;（4）调整工作之间的逻辑关系;（5）重新评估某项工作的持续时间;（6）对资源的投入进行调整。

实际工作中，调整非关键工作的工作时差是与资源投入优化相关的，工作在计划的最早开始时间到最迟开始时间之间开工，不会对总工期造成影响。增减工作项目关系到合同范围的调整，而减少项目的非关键工作常常由其他的施工单位承担施工，对压缩总工期影响不大。减少关键线路上的某项工作或工作中的某个工序是关系到工程项目质量的大事，极可能违反相应的国家标准、行业标准，即使压缩了总工期而提前竣工，也会给日后项目运营埋下隐患，是得不偿失的举措。

调整工作之间逻辑关系的应用机会是比较有限的，工作之间的技术逻辑是客观存在的，例如土方开挖—打垫层—钢筋绑扎—模板支护—浇灌混凝土之间的前后逻辑是难以调整的。调整工作的组织逻辑关系往往会带来成本的增加，因此这种方法可应用的机会有限。

因此，重新估算某项工作的持续时间，调整原计划的资源投入，压缩工作的持续时间是应用最广泛的调整内容。

在压缩总工期，实现项目提前投产为目的的计划调整中，首先要找出进度计划中的关键线路，压缩关键线路上关键工作的持续时间，以达到压缩总工期的目的。压缩关键工作时应注意遵守以下原则：（1）不能通过压缩关键工作而使关键线路变成非关键线路。这是为了避免在压缩关键工作上投入过多资源，而没有达到缩减总工期的目的;（2）选择关键线路上压缩时，单位时间成本增加值最低的工作优先进行压缩，这是资金价值最大化的内在要求;（3）每项关键工作都有不可继续压缩的持续时间最小值，这是工作的技术要求和限制，例如混凝土的固化增强时间是不可随意压缩的。

3  常见压缩参数的现实局限性

3.1  工作压缩单位时间成本增加值为恒定数值的局限性

实际工作中，在对项目的某项关键工作进行单位时间压缩成本增加值的计算时，常用某一恒定参数。恒定参数考虑了成本构成中的可变成本，可能忽略了固定成本的均摊，与实际不符。例如，不增加工人数量，仅增加工作时间实现压缩工期1天，需增加成本1万元，即单位时间成本增加值为1万元/日，那么，此工作压缩工期10天，需要增加的成本会大于10万元。这是由过多劳动时间导致工人劳动生产率下降，单位时间产出工程量减少，加班工资提高等原因造成的[3]。

3.2  不同工作的工期压缩措施实施后的成功概率不同

理论上，如果对工作A进行工期压缩的单位时间成本yA大于对工作B进行工期压缩的单位时间成本支出yB，如工作A工期压缩1天增加支出3万元，工作B工期压缩1天增加支出5万元，就应优先对低成本的工作A进行工期压缩。在实际工作中，这个决策忽略了风险对工期实现的影响。

4  考虑可变时间成本和风险的分析方法

鉴于恒定参数的现实局限性，引入压缩单位时间成本增加值y为所压缩工期第x日的函数关系来表示：

y=f（x）                                     （1）

那么壓缩工期后，成本增加支出C的计算为单位时间成本增加函数对时间x做定积分：

C=∫f（x）dx                                  （2）

在项目进度计划中，存在不同区域、不同专业的多个施工队之间的交叉施工或平行施工，会出现多条关键线路并存，压缩方案的成本计算需要对某几个工作组合进行对比，成本支出可计算为：

C=∫[f1（x）+f2（x）+…]dx                     （3）

决策树分析法是在已知各种情况发生概率的基础上，通过构成决策树取最大净值来判断可行性进行决策的方法。本文利用决策树法来计算可变成本和风险对可期值的影响，代替以往用恒定的时间成本来计算的方法，使问题的分析更加贴近实际，提高工期优化决策的科学性。

5  工程实例分析

5.1  项目概况

华北某电厂对烟气余热利用系统改造，本文截取一号机组进入停机检修阶段的一个局部片段来分析。发电机组在停机检修前接到调度要求，由于该市其他电厂发生非计划停机，为保障居民用电和工业开发区企业用热需求，要求该电厂将原计划停机检修40天的工期压缩为34天，机组点火发电时间比原计划提前6天。该电厂要求施工单位加快施工进度，压缩停机检修工期，并承诺如实现提前6天完成检修工作，建设单位给予施工单位3万元/日的奖励，以补偿施工单位增加的成本。双方就压缩工期事宜达成了一致。

5.2  双代号网络进度计划

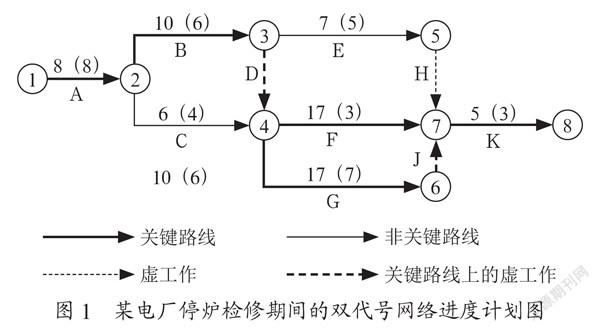
为方便分析，对实际项目进度计划图进行了大幅度简化，施工单位在停机检修阶段的双代号网络进度计划图如图1所示。

工作A：停炉、通风降温、拆除烟道;

工作B：烟道支撑钢结构的改造;

工作C：烟道悬挂钢结构的改造;

工作D、H、J：虚工作，表示技术逻辑关系;

工作E：换热器入口烟道的安装;

工作F：换热器出口烟道的安装;

工作G：烟道内部换热器的安装;

工作K：锅炉上水、点火、汽轮机冲转、发电。

图中工作箭线上部数字标示，如工作B处的10（6），括号外数字表示该工作的计划持续时间为10天，括号内数字表示该工作最少持续时间为6天，即该工作的持续时间不能够被压缩到6天以下。

5.3  关键工作的可压缩性及成本分析

下面对该网络进度计划进行工期压缩。首先找出该进度计划的关键线路：

共有两条：A—B—F—K，A—B—G—J—K;为方便压缩，将关键线路合并表示为A—B—F（G）—K，他们的计划工期为8+10+17+5=40天。

首先分析关键线路上的各个关键工作的可压缩性及成本情况：

工作A的持续时间为8天，包括停炉、拆除烟道等。为保护锅炉，停炉降温应严格按照停炉规程工作，工作A的最低工作时间为8天，工作A不可压缩。

工作B为烟道支撑座钢结构的改造，可以通过增加工人数量，延长劳动时间的方式予以压缩工期。经过测算，该工作由10天最多可压缩至6天，压缩工期第x天会造成的成本增加值与压缩天数的关系为：

y=0.1x+1                                    （4）

其中，x是压缩天数;y是压缩第x天所付出的成本支出（万元，下同）。

在工作B采取了赶工措施后，影响进度的风险因素较少，该工作在顶棚覆盖范围内工作，不受恶劣天气影响;生产工器具简单且充足;消耗辅材供应充足。经测算，采取赶工措施后，该工作赶工成功概率为0.90，失败概率为0.10，如赶工失败，将每天损失1万元。

工作F为安装换热器的出口烟道，该工作安装难度大，危险性高。拟采用工人三班倒24小时作业方式，原定1台汽车吊增加为2台，以满足加快的烟道构件的吊装速度。原定工作时间由17天可压缩至13天。压缩第x天工期会造成的成本增加值与压缩天数的关系为：

y=-0.15x+0.5                                （5）

工作F受到设备供货、大型吊车机械故障等大量风险因素的影响，尤其是风雨等恶劣天气的影响，经测算，若采取赶工措施后，该工作赶工成功概率为0.60，失败概率为0.40，如赶工失败，将每天损失0.3万元。

工作G为换热器内部件安装工作，作业面充足，可增加新的施工队，延长劳动时间，不用新增施工机械。据测算，原定工作时间由17天可压缩至7天。压缩第x天工期会造成的成本增加与压缩天数的关系为：

y=0.05x+0.6                                 （6）

经测算，采取赶工措施后，该工作赶工成功概率为0.90，失败概率为0.10，如赶工失败，将每天损失0.6万元。

由于工作F与工作G在工期压缩中是一个组合，因此工作组合F（G）的成本可以合并为：

y=0.05x+0.6-0.15x+0.5=-0.1x+1.1           （7）

工作组合F（G）的赶工成功概率为0.60×0.90=0.54，失败的概率为1-0.54=0.46。

工作K为机组点火过程，经建设单位同意，施工单位此工作可由5天压缩至3天，且不考虑风险。

5.4  工期压缩过程

经上述分析得知，在关键线路上，工作A不可压缩，工作B可压缩，工作组合F（G）可压缩，工作K可压缩且不增加成本。

第一步压缩过程：首先压缩工作K，将工期由5天压缩为3天。

显然，网络计划的关键线路未发生变化，总工期由40天减少为38天，距离34天的工期要求还超出4天。

第二部压缩过程：工作B可压缩4天，压缩工期第1天的成本支出可计算为：

万元                  （8）

压缩工期4天的收益为：

万元                    （9）

工作B的赶工成功概率为0.90，失败的概率为0.10，失败时的收益为-1×4=-4万元，即增加支出4万元。

工作组合F（G）可压缩4天，收益为：

万元                （10）

赶工成功的概率0.54，失败的概率为0.46，失败时的收益为：

-（0.3+0.6）×4=-3.6万元，即增加支出3.6万元。

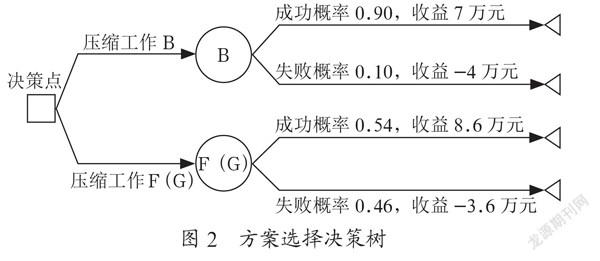
画出决策树，如图2所示。

通过计算，选择压缩工作B的期望收益是7×0.9-4×0.1=5.9万元;选择压缩工作组合F（G）的期望收益8.6×0.54-3.6×0.46=2.988萬元。压缩工作B的期望收益较高，施工单位决定选择工作B压缩4天工期。

压缩工作B后，重新找出网络计划的关键线路A—B（C）—F（G）—K，总工期为8+6+17+3=34天，符合工期要求。

4.5  实际效果验证

上述讨论的是该电厂的一号机组的停机改造计划，虽然停机期间遇到长达一周的连续强降雨，但是由于选择了成功概率高、成本支出高的方案，仍然按照既定工期完成工作，实现了机组的准时并网发电。如果不考虑风险，按照传统的压缩工作B比工作F（G）的收益低，而选择压缩工作F（G），会因为恶劣天气而导致不能实现工期目标。

在次年的二号机组检修时，由于设备、材料已全部到货，停机时机选在晴朗少雨的四月份，大大降低了工作组合F（G）的风险系数，施工单位重新评估了优化方案，调高了工作F和G的成功概率，选择了压缩工作组合F（G）的方案，取得了预期的收益，在此不再赘述。

5  结  论

本文分析常用的工期压缩方案中忽视时间成本支出不平衡和风险因素的问题，引入用成本与时间函数，结合压缩方案的成功概率，用决策树法作为工具来分析一个具体实例，在恶劣天气的情况下实现了工期目标，取得了预定的效果。决策树法能够帮助施工单位在面对变化的外部条件风险时选择更好的方案。决策树法是施工单位在进行施工方案选择时的有效工具，为方案决策提供了更多依据。

本文还有很多不足之处，在分析成本与压缩时间的关系时，为分析方便，简单用了一元函数，与实际情况尚有较大误差。在决策树法的应用时，每种方案的成功概率的取值决定了最终的计算结果。对概率取值的分析需要用查阅历年资料、专家意见、头脑风暴等更加丰富的方法谨慎地确定成功概率，以提高决策的科学性。

参考文献：

[1] 江建军.网络计划技术在建筑工程施工管理中的应用问题 [J].运筹与管理，2000，9（3）：123-126.

[2] 全国一级建造师执业资格考试用书编写委员会.建设工程项目管理 [M].北京：中国建筑工业出版社，2011.

[3] 全国造价工程师执业资格考试培训教材编审委员会.建设工程造价管理 [M].北京：中国计划出版社，2013.

[4] 郑碧贞，李学玲.决策树法在建筑工程投标决策中的应用 [J].科技创新与应用，2013（34）：226.

作者简介：陈旭（1983.04-），女，汉族，湖北天门人，硕士，工程师，研究方向：管理工程。