基于压缩感知的MIMO-OFDM信道估计中的导频设计方案

周煜澄 何雪云 梁 彦

（南京邮电大学通信与信息工程学院，南京，210003）

引 言

多输入多输出-正交频分复用(Multiple input multiple output-orthogonal frequency division multiplexing，MIMO-OFDM)能有效地抵抗无线传输系统中的多径效应，并提高频谱利用率。而信道估计作为MIMO-OFDM通信系统的关键技术之一，也受到了广泛的研究。近年来新兴的稀疏信道估计也被称为压缩信道感知，利用无线信道的稀疏性，将压缩感知(Compressed sensing,CS)技术[1-3]应用到信道估计中。与传统的最小二乘(Least squares,LS)和最小均方误差(Minimum mean square error,MMSE)信道估计方法相比，压缩感知技术能有效减少导频开销，并且提高频谱利用率和信道估计的精度[4-6]。目前，正交匹配追踪(Orthogonal matching pursuit,OMP)，压缩采样匹配追踪(Compressive sampling matching pursuit,CoSaMP)以及基追踪(Basis pursuit,BP)等算法已被应用到OFDM系统的稀疏信道估计中，相比LS和MMSE取得了更优的信道估计性能[7-9]。

在传统的信道估计中，导频符号均匀放置在OFDM系统的子载波上通常是最优的，然而在基于压缩感知的信道估计中，该结论并不成立，其导频符号和导频位置的设计方法与传统的信道估计不同。文献[10]提出的随机序贯搜索(Stochastic sequential search，SSS)算法用于解决基于压缩感知的OFDM信道估计中的导频优化[11]问题，考虑以最小化观测矩阵的互相关为目标进行优化，通过改变外循环和内循环次数，对导频序列的每个位置进行替换和优化操作，并将此算法拓展到MIMO系统中，提出两种导频优化方案。然而，此方案在天线数增加后无法保证每个天线都能获得满意的导频设计。本文结合文献[10]提出的基于遗传算法和移位机制的导频分配理论，对SSS算法进行改进，提出随机搜索移位(Stochastic sequential search-shift mechanism，SSS-SM)算法。仿真结果表明，在相同条件下，同SSS算法相比，SSS-SM算法能以更低的算法复杂度获得更优的导频位置设计，该设计可以使得信道估计性能更优。

1 系统模型

对于一个MIMO-OFDM系统，定义Nu为发射天线数，Nv为接收天线数。假设一个OFDM系统具有N个子载波，其中Np个导频子载波用于频域导频辅助信道估计，假定则=表示第i根发射天线的导频图案。为不失一般性，假设假设对于i≠l，p(i)∩p(l)=∅ ，即不同发射天线的导频图案相互正交，因此，接收机可以对来自每个发射天线的信道执行独立的稀疏信道估计。这样的信道可以建模为一个有限脉冲响应（Finite impulse response，FIR）滤波器

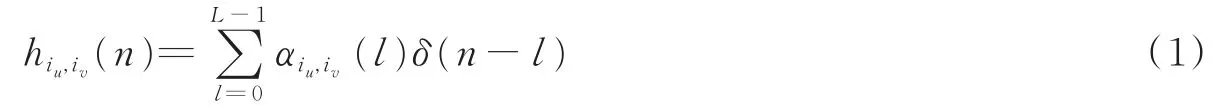
式中：L表示信道抽头的总数，αiu,iv(l)表示第l个信道抽头的复增益。对于稀疏度为K的信号而言，向量只有K个非零元素且K≪L。则第iv根接收天线上获得的接收信号可以表示为

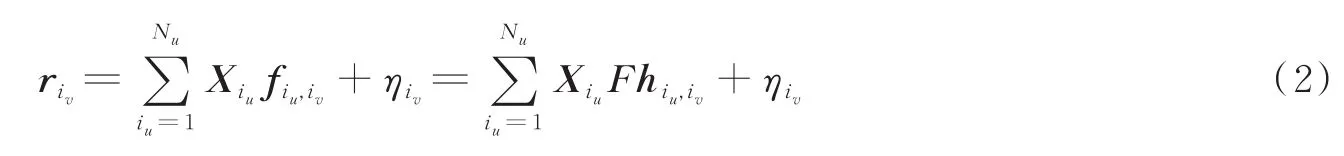
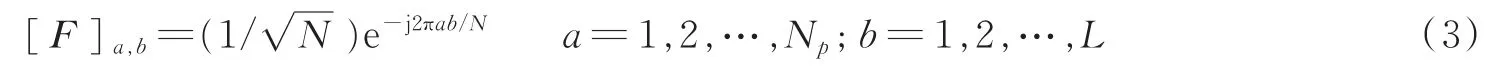
为保证每对接收与发射天线之间较好的信道估计性能，当第i根发射天线发送导频时，其他发射天线将不会向任何用户发送数据或导频，即x()=0(n=1,…,Np；1≤i,j≤Nu；i≠j)。则第iu根发射天线和第iv根接收天线之间的导频图案可以表示为

式中：Siu∈CNp×N是从一个N×N的单位矩阵中抽取行号为导频位置索引的Np行得到的，为一个选择矩阵，它可以从一个N维向量中选取与导频位置相对的元素。同时由于等式成立，于是式（3）可以改写为

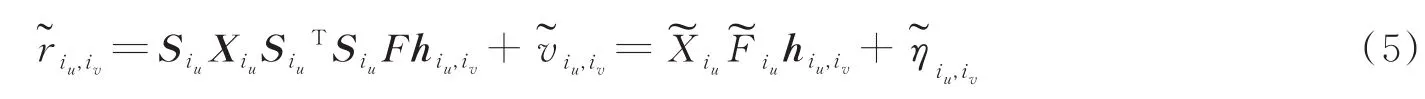
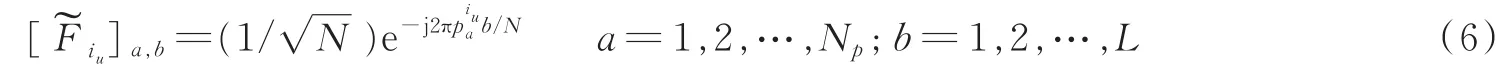
然而，由于更关注Np＜L的情形，在此情形下可以节约更多的导频从而提高数据传输速率。实际上，由于采样周期通常远小于信道时延扩展，hiu,iv的大部分都是零或者接近零，即hiu,iv为一个稀疏向量。在此先验条件下，可以使用比未知信道系数更少的导频，即Np＜L，并且通过CS算法来估计hiu,iv。大量研究已经证明在信道估计中CS算法性能优于LS算法[12]。然而,在基于压缩感知的信道估计中,导频设计问题与传统信道估计中的方法并不相同,需要专门研究。

2 导频优化

2.1 OFDM信道估计中的导频优化准则

在单天线的OFDM系统中，发射天线数Nu和接收天线数Nv皆为1，可将式（7）简化为

式中：r为接收导频符号构成的向量，Np×1维；A=XF，X为由发送导频构成的对角阵，Np×Np维；F为一个Np×L维的傅里叶子矩阵；h为等效的离散信道冲击响应，L×1维；η表示OFDM子载波上的加性高斯白噪声，Np×1维。

CS研究的最新进展表明，在无噪条件下，当测量矩阵A满足有限等距性（Restricted isometry property，RIP）[13-14]时，利用测量矩阵r能以很高概率重建h。然而，目前没有方法可以从多项式复杂度上检验一个给定矩阵是否满足RIP。另外，根据文献[15]，可以最小化A的相关性，即互不相干特性（Mutual incoherence property，MIP）。MIP条件更强于RIP，因为MIP满足RIP，反过来却不一定[16]。此外，MIP比RIP更加直观，更加实际。因此，本文将MIP作为导频设计准则。

在OFDM系统中，对于给定的导频图案p={p1,p2,…,pNp}，其中1≤p1≤p2≤ … ≤pNp≤N，定义A的相关性为A的任意不同两列之间的最大绝对相关，即

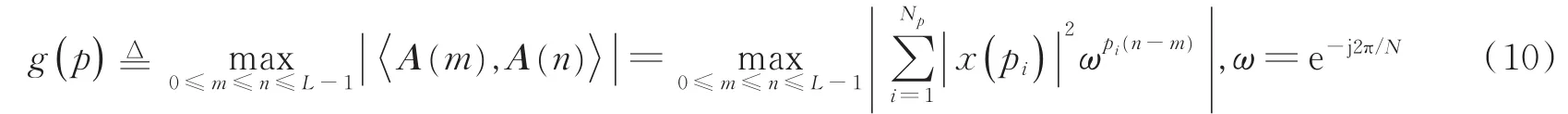
对于导频图案p，此目标函数用于最小化A的相关性，即

求解式（7）中的最优问题，即最优导频图案，可以表示成

假设所有OFDM导频符号的传输功率相同，即

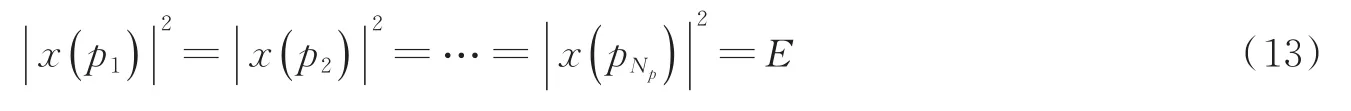
2.2 OFDM信道估计中基于SSS算法的导频优化方案

直观地说，通过穷举搜索所有可能导频图案的方法，可以获得最小MIP的最优导频图案。然而当N和Np不是很小时，很难通过计算搜索所有（N，Np）个候选集,因为该搜索空间非常庞大。显然，由于要占用大量的计算资源，穷举搜索对于未来的节能无线系统来说并不是一个好的选择[17]。

针对任意给定的（N，Np）的组合以及L的值，文献[10]提出了一种导频优化方案SSS。这是一种基于随机搜索的导频优化方案，通过两层迭代循环来搜索次最优的导频图案。首先确定外循环和内循环的最大迭代次数，即M1和M2。

在每次外循环的迭代中，随机生成一个导频图案p⊂N={1,…,N}作为内循环的初始化。在内循环的每次迭代中，根据以下步骤对p的每个位置进行有顺序的更新。

在k=1,…,Np次循环中，对于从上一次迭代中获得的最新p，以最小化MIP为准则从序列N{p(i)|i=1,…,Np,i≠k}选取一个最佳位置来更新p的第k个位置。经过第k个位置更新的结果导频图案p^在数学上可以表示为

在求出之后，令p=。对于外循环的每个初始导频图案，最终得到一个相应的导频图案。在M1次外循环中，得到M1个最优结果，并从中选取MIP最小的一个作为最终结果输出。

2.3 MIMO-OFDM信道估计中的导频优化方案

2.3.1 基于ES2算法的导频优化方案

文献[10]将SSS算法扩展到MIMO系统中进行改进，提出了一种通过联合设计以达到一定公平性的改进算法ES2。为不失一般性，为Nu根发射天线设计Nu个正交导频图案，表示为

在w的定义中存在着一种隐式顺序，即p(i)={w((i-1)Np+1),…,w(iNp)}。然而，每个特定的p(i)中位置的顺序并不重要。于是，把此联合导频设计的目标函数定义为Nu个导频图案的加权和相关，表示为

式中：bi为第i根传输天线的权重。此联合设计方案的目的就是寻找最小的目标函数值w，可表示为

ES2算法由1个外循环和两个内循环组成。令M1，M2和M3分别表示外循环次数、第1个内循环次数以及第2个内循环的次数。ES2的具体算法如算法1所示。

算法1基于SSS的MIMO联合导频优化算法（ES2）

步骤 1初始化阶段：M1为外循环次数，M2为第1个内循环次数，M3=NpNu为第2个内循环次数。D=0M1×M3用于存放导频序列，v=0M1用于存放D中的导频序列对应的ζ(w)。

步骤2迭代循环阶段：

(1)外循环阶段：在每次外循环l中，从子载波集合c中随机选取M3个元素，构成导频序列w，=。跳转至(2)内循环阶段。w存放至D的第l行，并将w对应的ζ(w)存放至v的第l个元素位置。

(2)内循环阶段：

①SSS步骤：在每次内循环中，若w与相同，跳出内循环；否则进行逐位优化(对于w的每个导频位置索引m=1,2,…,M3,保持w中除了第m个元素以外的其他M3-1个元素不变，对w的第m个导频索引位置选取优元素，具体方法与SSS相同，计算ζ(w)的最小值ζ(w*)以及对应的w*，w=w*。)。将w的每一个元素赋值给，跳转至①排列步骤。

②排列步骤：对于每一次内循环，若w与相同，跳出内循环；否则进行排序优化(对于w的每一个位置m=1,2,…,M3，依次交换第m个元素位置与其他天线上的每个元素位置，并计算目标函数ζ(w)，从中选出最小值ζ()以及对应的，w=。)。将w的每一个元素赋值给w^。

步骤3结果输出阶段：从v的所有M1个元素中选出最小值，输出矩阵D中对应的导频序列，即为导频优化结果。

2.3.2 基于改进的SSS-SM算法的导频优化算法

基于SSS的ES2算法将导频优化问题转化为求解最小目标函数的问题，通过多层迭代循环来搜索次最优的导频图案，相对于穷举算法而言节约了大量的计算资源。然而，多层嵌套的循环搜索对于计算资源有限的无线通信系统仍是巨大的负担，并且ES2排列步骤中交换w序列位置的方法无法保证每根传输天线都能获得最优的导频图案。

本文结合文献[18]提出了移位机制理论，并对SSS算法进行改进，提出了SSS-SM算法。移位机制能够使所有导频位置集合具有尽可能小且全部相同的互相关值。下面将对移位机制进行详细介绍。

定理1将第1根发射天线的导频图案Λ1={y1,y2,…,yP}作为核心导频图案，元素排列顺序为升序，若其他发射天线上的导频图案满足Λiu={y1+iu-1,y2+iu-1,…,yP+iu-1},iu=2,…,Nu。那么所有导频位置集合Λiu,iu=1,2,…,Nu将有相同的互相关值，即μiu=μ1,iu=2,…,Nu。

定理1的证明参见文献[19]。结合以上的移位机制理论，提出了SSS-SM算法。SSS-SM主要思想为首先通过SSS算法搜索出满足最小MIP的最优导频图案p，并将p作为第1根发射天线的导频图案，其余发射天线的导频图案皆为p的移位，即p(i)={+i-1,+i-1,…,+i-1}，i=1,…,Nu。导频集合即为Nu根发射天线的最优导频图案。SSS-SM的具体算法如算法2所示。

算法 2随机搜索-移位算法（SSS-SM）

步骤 1初始化阶段：发射天线数Nu，外循环次数M1，内循环次数M2，D=0M1×Np用于存放导频序列，r=0M1用于存放D中M1种导频序列对应的g(p)。

步骤2循环迭代阶段：

(1)外循环阶段：在每次外循环中，从子载波集合N中随机选取Np个元素，构成导频序列p=0Np。跳转至(2)内循环阶段。p存放至D的第l行，并将p对应的g(p)存放至r的第l个元素位置。

(2)内循环阶段：在每次内循环中，若p与相同，跳出内循环；否则跳转至 (3)逐位优化阶段。=p。

(3)逐位优化阶段：对于p={p(1),p(2),…,p(k-1),p(k),p(k+1),…,p(Np)}的每个导频位置索引k=1,2,…,Np，保持除第k个元素以外的k-1个元素不变，候选集为Λ=N{p(i)|i=1,…,Np,i≠k}，每一次将Λ的每个元素放到第k个位置上，计算g(p)的最小值g(p*)以及对应的，令p=。如果相邻导频位置间隔小于Nu，则跳出此循环。

步骤3结果输出阶段：从r的所有M1个元素中选出最小值，将矩阵D中对应的导频作为第1根发射天线的导频p(1)，其他发射天线的导频皆为p(1)的移位，即p(i)={+i-1,+i-1,…,+i-1},i=2,…,Nu。最后输出结果导频图案

在SSS-SM中，将MIMO系统中搜索多发射天线最优导频图案的问题等效为使用SSS求单根天线的最优导频问题，此方案既保证了每根发射天线都满足最小的MIP，又节省了大量的计算时间和计算资源。

2.3.3 ES2算法与SSS-SM算法复杂度分析

从算法复杂度来比较，两种算法中主要的计算量皆为计算目标函数值部分，ES2的目标函数为ζ(w)，而SSS-SM的目标函数为g(p)，由式（12）可知，ζ(w)为Nu个g(p)的加权和，于是通过统计两种算法计算目标函数g(p)的次数来估算算法复杂度。ES2算法计算g(p)的次数为：M1×M2×Np××N；SSS-SM算法计算g(p)的次数为：M1×M2×Np×(N-Np+1)，由于Np≪N，则可以近似为M1×M2×Np×N。通过此方法估计的算法复杂度，ES2约为SSS-SM的倍，因此，随着发射天线数的增加，ES2计算目标函数的次数也在增加，在发射天线越多的情形下，占用的计算资源也越多；而SSS-SM由于只需要优化第1根发射天线，所以其计算目标函数的次数与发射天线数无关，可以很好地适应MIMO-OFDM系统。

3 仿真分析

3.1 重建性能的比较

对于一个MIMO-OFDM系统，假设子载波数目N=512，最大时延对应的抽样时间倍数L=50，信道稀疏度K=6,每根发射天线的导频数Np=24，Nu为发射天线数，Nv为接收天线数，外循环次数M1=200，内循环次数M2=100。使用SSS-SM和ES2进行导频优化，将生成的导频应用于系统并使用OMP算法进行信道估计，通过信道估计的均方误差（Mean square error，MSE）来比较两种算法获得的导频性能的优劣。很明显，好的导频将使得信道估计的MSE更小。在发射天线数Nu=4时，使用以上两种算法获得的导频对应的信道估计MSE如图1所示。在0～5 dB的低信噪比情况下，SSS-SM的MSE比ES2高约0.6 dB；而随着信噪比的提升，SSS-SM的MSE下降更快。图1中出现MSE的交点说明同ES2算法相比，由SSS-SM算法获得的导频在高信噪比的条件下更容易获得较低的MSE。将发射天线数Nu增加至8，如图2所示，低信噪比情况下，两者几乎相等；随着信噪比的增加，SSS-SM的MSE下降更为明显，SNR为35 dB时，相比ES2的MSE低约5.5 dB。可以看出，两种算法性能比较接近，随着天线数的增加，SSS-SM获得的导频更具优势。

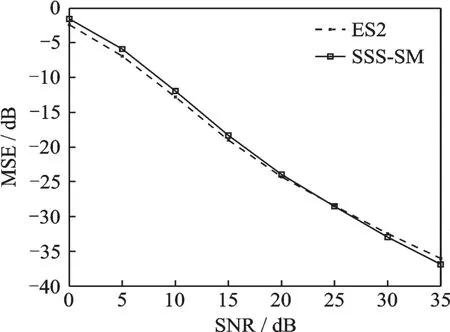
图1 Nu=4时SSS-SM和ES2的MSE比较Fig.1 Comparison of MSE between SSS-SM and ES2 with Nu=4

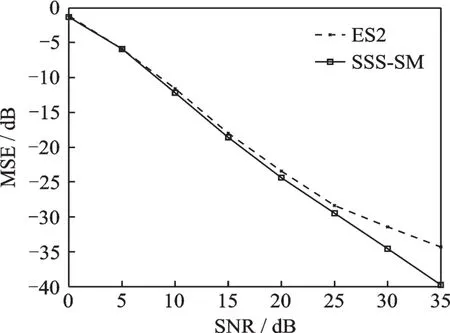
图2 Nu=8时SSS-SM和ES2的MSE比较Fig.2 Comparison of MSE between SSS-SM and ES2 with Nu=8

3.2 算法复杂度比较

本文通过研究算法复杂度来比较两种算法的性能。通过统计计算目标函数g(p)的次数来比较两种算法的算法复杂度。外循环和内循环次数分别为M1=200和M2=100，在发射天线数Nu=4和8时，SSS-SM和ES2计算目标函数的次数如表1中所示。从表1中可以看出，Nu=4时，ES2计算目标函数的次数是SSS-SM的16.8倍左右，Nu=8时约为67倍。

表1 ES2和SSS-SM算法复杂度比较Tab.1 Comparison of algorithm complexity between ES2 and SSS-SM

综合以上两点可以得出结论，SSS-SM能以更少的计算复杂度获得与ES2性能相似的导频图案设计。因为将两种算法获得的导频应用到系统中，比较它们各自的信道估计性能发现，二者信道估计性能比较接近；在多天线高信噪比情况下，SSSSM的MSE比ES2平均低约3～5 dB，表明SSS-SM算法获得的导频在多天线高信噪比条件下能取得更优的信道估计性能。

4 结束语

本文首先研究了基于压缩感知的OFDM系统的导频优化问题，将信道估计问题转化为压缩感知理论中的稀疏信号重建问题，将最小化测量矩阵的互相关作为导频优化的目标，并将此思想扩展到MIMO-OFDM系统中。着重介绍了已有的SSS及ES2两种算法，并针对其优缺点进行改进，结合移位机制提出了SSS-SM算法。仿真结果表明，SSS-SM算法相较于ES2具有更低的算法复杂度，可以节约大量计算时间并达到与ES2相近的导频优化性能；并且随着发射天线数增加，在高信噪比情形下，SSSSM的MSE比ES2平均低约3～5 dB。这表明对于计算资源极其有限的MIMO-OFDM系统，SSS-SM算法具有更大的优势与发展前景。