大规模MIMO系统上行链路中改进的混合迭代检测算法

季荣峰 何雪云 梁 彦

（南京邮电大学通信与信息工程学院，南京，210003）

引 言

与传统多输入多输出(Multiple-input-multiple-output，MIMO)相比，大规模MIMO在基站配置数十甚至数百根天线[1]。天线数目的增加大大地提高了系统的能源和频谱效率，达到2～3个数量级，大规模MIMO也因此成为5G的热点研究方向之一[2-3]。

作为最优的检测算方法，最大似然（Maximum likelihood，ML）算法[4]存在复杂度随天线数量的增多呈指数规律增长的缺点。最小均方误差（Minimum mean square error，MMSE）算法[5]因为加入了计算量为O(K3)的矩阵求逆运算，效果也不理想。为了简化MMSE算法中的矩阵求逆运算，文献[6]利用了Neumann级数方法，但是当展开级数超过2时复杂度太高，达到O(K3)。文献[7]将高斯-赛得尔（Gauss Seidel，GS）迭代方法应用到检测中，避免了高复杂度，同时得到了接近最优的检测性能。文献[8]提出了一种混合迭代算法，其复杂度低至O(K2)，并且利用最速下降（Steepest descent，SD）算法为GS迭代提供有效的收敛方向，加快收敛速度，提高检测性能。

此外，检测的判决都有涉及到用于信道译码器的对数似然比(Log likelihood ratio，LLR)，它的计算需要用到后验信号噪声及干扰比(Signal to interference plus noise，SINR)。现在大部分的研究都利用初始迭代SINR来完成所有迭代判决，因此有着显著的性能损失。本文改进了LLR的近似计算方法，使SINR随着迭代次数m更接近精确SINR，从而改善了检测性能。

1 系统模型

本文主要研究大规模MIMO系统的上行链路，在基站配备N根接收天线，同时服务K个用户（N≫K）。令y∈CN×1表示基站端接收到的信号矢量，x=[x1,x2,…,xK]∈CK×1表示K个用户发射的信号矢量，这里xk∈Q是来自第k个用户的发送信息，Q为调制符号集。H∈CN×K表示信道矩阵，则接收信号y可以表示为

式中：n表示0均值、方差为σ2的N×1维加性高斯白噪声矢量。

1.1 MMSE检测算法

经过MMSE信号检测，基站端对发射信号的估计为

式中^=HHy。MMSE检测器的滤波矩阵W可表示为

式中：G=HHH是格拉姆矩阵，W-1是MMSE算法复杂度高的主要原因，其计算量达到O(K3)。

1.2 对数似然比的计算

信道译码时会涉及到对数似然比LLR。令U=W-1G代表均衡后的等效信道矩阵，Ui,j为U的第(i,j)个元素。令E=W-1HH(W-1HH)H=W-1GW-1，Ei,i为矩阵E的第i个对角元素。由MMSE加权矩阵处理后的均衡信号为

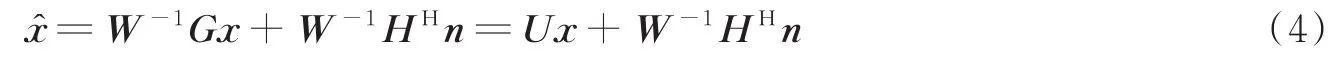
所以第i个用户所发送的符号估计值为=^=ρixi+λi，这里ei表示K维单位矩阵的第i个列向量，ρi为均衡后的等效信道增益，可表示为

λi表示噪声加干扰项（Noise plus interference term，NPI），方差为，分别可表示为

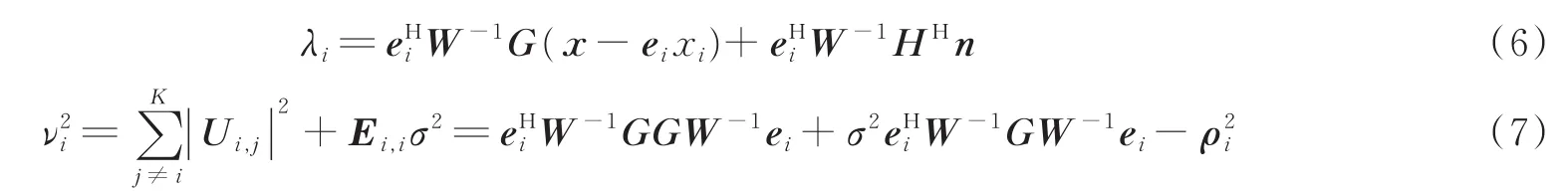
根据文献 [9]提出的max-log近似方法，能够得到第i个用户发送的第b个比特的对数似然比Li,b，即

式中：γi=/为第i个用户的SINR，和分别表示第b位为0和1的调制符号集。

2 低复杂度检测算法

2.1 Gauss Seidel算法

在解N维线性方程Ax=b时,利用GS算法可以避免矩阵求逆。这里A为N×N维对称正定矩阵，x和b分别为N×1维的解向量和测量向量。所以GS算法可以解决MMSE算法中W-1的计算，对于大规模MIMO上行链路，由于信道矩阵H符合满秩并且列渐进正交的条件，因此滤波矩阵W是对称正定矩阵[4]，可将W分解为

式中：D为W的对角矩阵，L和LH分别为W的严格下三角和严格上三角矩阵。所以利用GS算法对信号矢量x^可估计为

2.2 改进的混合迭代算法

文献[8]利用SD算法在迭代开始就能有很好搜索方向的特性[10-11]，在基于GS算法的基础上提出了一种复杂度低的混合迭代算法，称为SDGS算法。SDGS算法能快速收敛并且获得接近MMSE算法的检测性能。SDGS用SD算法来表示前面两次GS迭代。SD算法的第一次迭代可以表示为

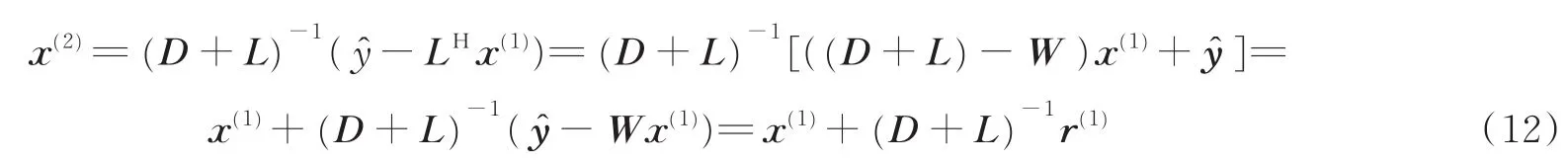
式中r(1)=-Wx(1)=r(0)-up(0),把SD和GS迭代合并可得到

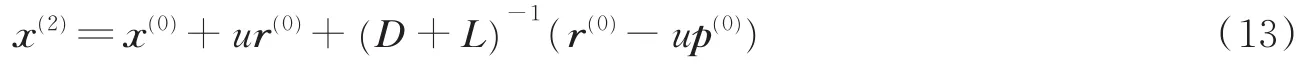
将GS的前两次迭代表示为式(13)，更新为混合迭代值=x(2)，然后利用式(10)执行接下来的m-1次迭代。

2.3 近似对数似然比计算

根据式（8）可以发现求对数似然比Li,b时，必须再次涉及到W-1。为了降低复杂度，文献[7-8]利用W的对角占优特性用D-1来代替W-1，得到近似等效信道增益和NPI方差，分别表示为

2.4 改进的对数似然比的计算

2.3节介绍的近似对数似然比计算直接用D-1代替W-1，避免了求逆运算，但是会有较大的性能损失。所以根据纽曼级数展开定理，把W-1按纽曼级数展开，根据迭代次数取前m项得到近似值，再取其对角元素矩阵。由于比D-1更接近W-1，所以得到的近似等效信道增益和NPI方差也更精确，最后求出SINR代入式（8）可得到更精确的Li,b，从而提高了检测性能。

式(7)可重写为

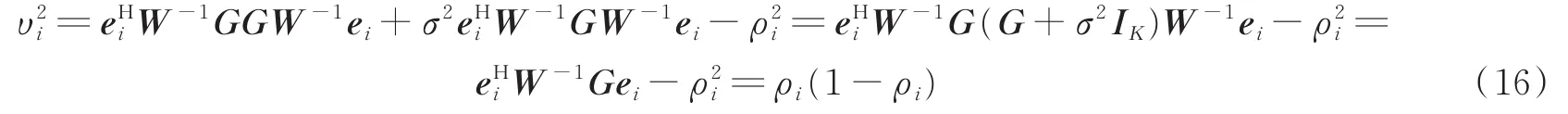
从式(16)可以看出，NPI方差可以用等效信道增益ρi来表示，式(5)可重写为

由于W对角占优，用D-1来代替W-1可分别得到近似等效信道增益和NPI方差，即

定理1（Neumann级数展开[12]）：对于一个K维矩阵P，同时满足条件非奇异和，则(IKP)也是非奇异的，它的逆可以表示为

对于大规模MIMO上行链路，信道矩阵可以看成是列渐进正交，因此G=HHH和W=G+σ2IK也是对称正定的，根据定理1，W可重写为在本文中，Q=D，D为W的对角元素矩阵，式（21）取前m项，得到

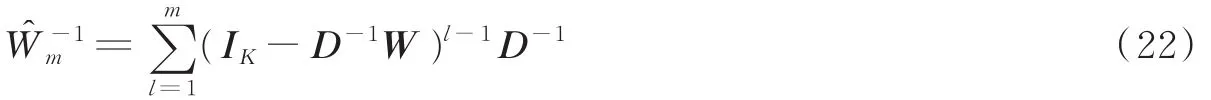
式中Q-1是一任意矩阵，满足

令θ=IK-D-1W，为的对角元素矩阵。dk,k为的第k个对角元素，和wk,k分别为W-1和W的第k个对角元素。

（1）当m=1时，=D-1，dk,k=≈。

（2）当m=2时，=D-1+θD-1,所以dk,k=≈+θk,k，其中θk,k为θ的第k个对角元素。

（3）当m=3 时，=D-1+θD-1+θ2D-1，所以dk,k=w′k.k≈+θk,k+θ′kθk，其中θ′k和θk分别为θ的第k个行向量和第k个列向量。

(4)当m≥4时，计算复杂度高达O(K3)，因此W^-1m(m≥ 4)=W^-13。

根据式(18)可得到近似等效信道增益，即

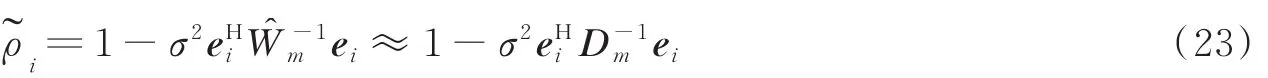
根据迭代次数取不同的，得到新的近似值和，代入后计算出更接近精确值的SINR，从而算出新的LLR。因此，改进后的LLR计算方法进一步提高了检测性能，在m很小时SDGS算法便能得到理想的结果。

3 仿真结果

本文给出了基于Matlab的仿真结果，系统配置为128×16（其中128为基站天线数，16为用户数），信道为相关瑞利衰落信道，相关系数为0.7。基带信号调制方式为64QAM，在接收端，信号解码方式为Viterbi解码。

3.1 不同检测算法的检测性能对比

图1比较了普通GS迭代和混合迭代SDGS算法的检测性能。由图1可见，在m同样时，SDGS算法的性能远优于普通GS迭代算法。图2对比了SDGS算法和改进LLR的SDGS算法的检测性能。从仿真结果可以看出，经过少量迭代，改进LLR的SDGS算法优于SDGS算法，并且它的性能曲线快速接近MMSE算法的性能曲线。比如，当迭代次数m=4时，想要达到BER=10-3的条件，SDGS算法需要8 dB左右的信噪比，而改进LLR的SDGS算法需要7 dB左右。

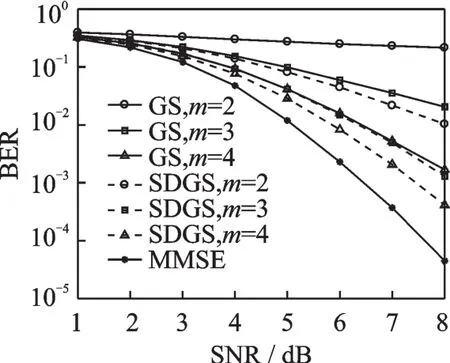
图1 GS迭代和SDGS算法的BER对比Fig.1 Comparison of BER between GS and SDGS

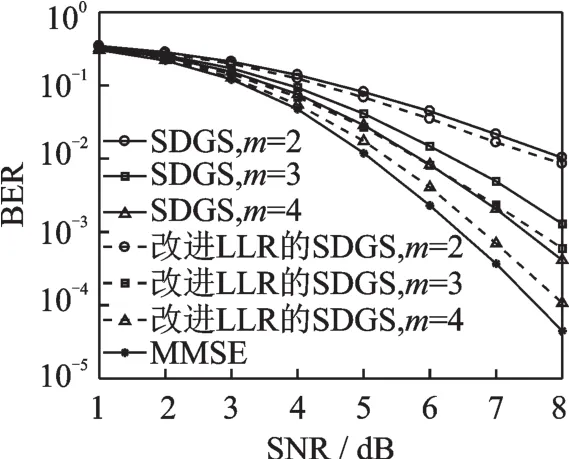
图2 SDGS和改进SDGS算法的BER对比Fig.2 Comparison of BER between SDGS and improved SDGS

3.2 信道的相关性对于检测性能的影响

MIMO系统中，检测性能受到信道空间相关性的影响。相关系数ξ（0≤ξ≤1）表示两个相邻天线之间的相关性[13]。从图3可以观察到，MMSE检测算法的性能随着相关系数的增大而变差。当相关系数ξ=0.5时，在相同迭代次数下，改进LLR的SDGS算法比ξ=0.7时的检测性能更逼近MMSE性能。为此，在ξ=0.7时可适当的增加迭代次数，如图4所示。

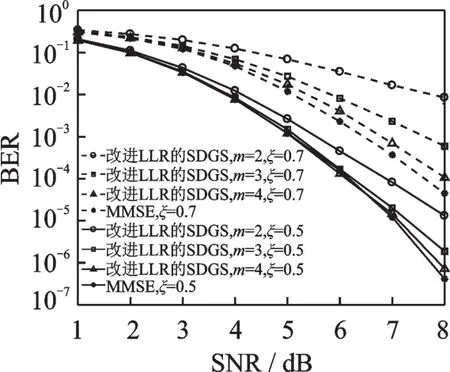
图3 相关系数分别0.5和0.7时的BERFig.3 Comparison of BER between ξ=0.5 and ξ=0.7

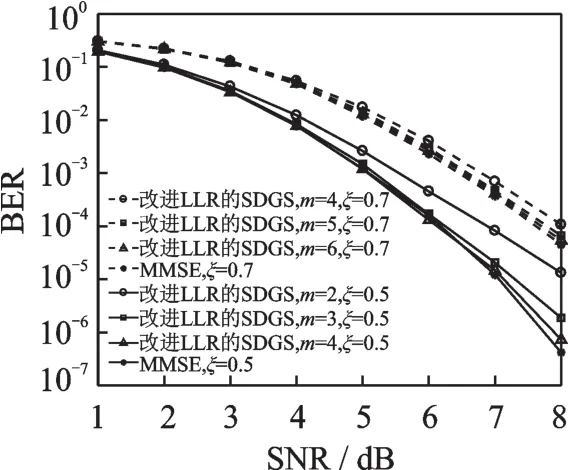
图4 增加迭代次数后的BER比较Fig.4 Comparison of BER after increasing the number of iteration

3.3 复杂度对比

由于所有的MMSE算法和本文提出的算法都有W=G+σ2IK和=HHy的计算，所以只考虑以下3部分：

（1）初始值和首次迭代：x(0)=D-1^需要K次乘法，首次迭代计算r(0)，p(0)和标量u，分别需要K2，K2和2K次。结合式（13）共需要2K2+6K次乘法。

（2）GS迭代部分：由式（10）得到一次GS迭代需要K2次乘法。

（3）LLR计算：主要来自于有效信道增益和NPI方差的计算以及的计算。计算ρi=1-和=ρi(1-ρi)分别需要3K和K次乘法，计算θ需要K2次，然后求dk,k，当m=2时为K次，当m≥3时为K2+2K次。

所以，改进LLR的SDGS算法的总体复杂度是O(K2)，与m有关，具体如表1，一般m都很小。表2给出了当SINR=8时，SDGS和改进LLR的SDGS算法在不同m下的BER以及恢复1 000比特所需要的时间。

表1 3种检测算法计算复杂度对比Tab.1 Complexity comparison between three algorithms

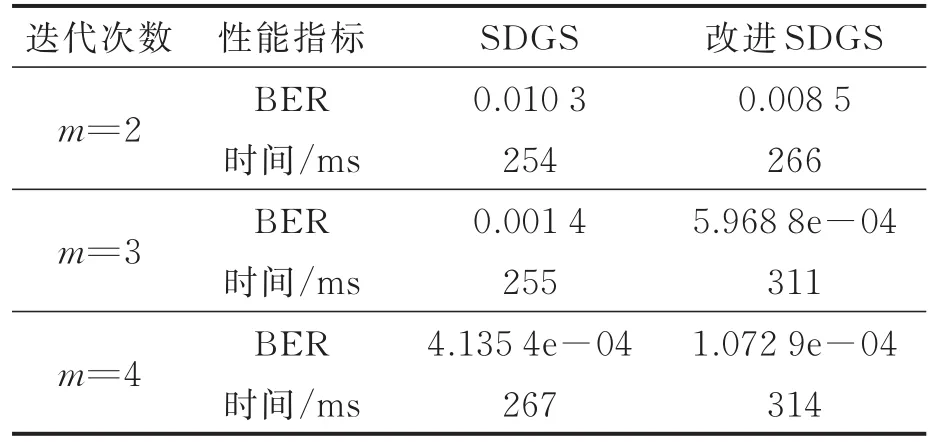
表2 两种检测算法的计算时间和BER对比Tab.2 Comparison of computing time and BER between two algorithms

4 结束语

在大规模MIMO系统中，虽然MMSE算法性能接近ML算法性能，但是因为复杂度太高（O(K3)）的原因很难应用在实际中。SDGS算法将复杂度降为O(K2)，同时检测性能比GS算法好。本文基于SDGS算法，提出了一种改进LLR的SDGS算法，检测性能得到了进一步提高，只需要少量迭代次数就可以获得接近MMSE的检测性能，同时，算法复杂度保持在O(K2)。仿真结果表明，对于大规模MIMO系统，所提出的改进LLR的SDGS算法具有更大的优势。