天津地区吹填淤泥非线性渗透特性试验研究
2019-09-06康亚静孙立强路江鑫
康亚静,孙立强,路江鑫
(1.河北省水利水电勘测设计研究院,石家庄050000;2.水利工程仿真与安全国家重点实验室 天津大学,天津300072;3.河北省水利厅,石家庄050011)
1 研究背景
当前,对吹填土地基进行变形计算采用的是常规固结理论,工程中出现的较大整体沉降、标高不足等实际问题表明,采用常规理论进行变形计算,计算值与实际沉降值存在较大差异。忽略设计施工偶然因素,主要有两方面原因:一是围海造陆工程中加固对象为吹填淤泥,其含水率、孔隙比都非常高,处于流动状态,属欠固结土;二是加固中的吹填淤泥应力状态由接近于零的小应力发展到最终固结应力,其固结排水特性与正常固结土差别很大。所以,采用常规理论或大应力状态下的渗透系数进行吹填土变形计算,与工程实际存在较大偏差。
国内外学者对软黏土渗透非线性特性做了大量研究。谢康和等[1]对萧山8个试样进行了一维固结渗透试验,讨论和总结了4种非线性渗透模型,分析了对应于4种非线性渗透模型的土性参数;路江鑫等[2]通过开展淤泥质吹填土压缩—渗透试验,得到了软黏土渗透性随土质和孔隙比之间变化的预测公式,并通过收集国内外26组数据进行了普适性验证;齐添等[3-4]对萧山软黏土进行了一维固结渗透联合试验,测定了基于孔隙比与渗透系数的e-logkv的非线性关系;孙立强等[5]基于吹填土非线性压缩—渗透特性,对未打穿砂井固结理论进行了研究;Pane[6]针对软黏土渗透性,探索了新型试验方法;Taylor[7],Mesri &Rokhsar[8],Moriwaki[9],Mes ri & Tavenas[10],Mesri &Choi[11],Tavenas[12]等分别考虑不同因素对软黏土渗透性影响,基于试验数据对e-lgkv模型适用范围进行了探讨,并对模型进行改进和完善。目前,不少学者对吹填淤泥非线性特性进行了研究,例如张明等[13-14]对深圳前湾含水率大于100%的吹填淤泥进行了固结渗透试验,并对试验数据进行回归拟合,进行了参数测定。以上研究大都基于某一特定地区的相同液限软黏土开展试验研究,对吹填淤泥渗透性研究较少,且模型试用性对于不同地区、不同液限土体不同,需要进行不同孔隙比下的固结—渗透试验来确定。
本文利用GDS固结仪对天津地区不同液限吹填淤泥开展连续的固结—渗透试验,通过试验得出吹填泥不同孔隙比下的渗透系数。采用4种非线性渗透模型对试验结果进行回归拟合,对比分析了模型参数,给出了适用于该地区吹填淤泥的最佳非线性渗透关系,进一步完善了该地区吹填淤泥非线性渗透特性研究,研究成果对天津地区吹填土地基实际固结计算具有重要意义。
2 试验方法
2.1 试验土样
将取自天津临港(TJLG)、南港(TJNG)、东疆港区(TJDG)吹填区的吹填淤泥调制成泥浆状并使其自然沉积,同时开展液塑限试验,得到吹填淤泥塑限和液限,自然沉积后试验土样物理指标如表1。

表1 吹填淤泥的基本物理参数
2.2 试验仪器及试验原理
本次试验采用固结—渗透试验GDS高级固结仪,克服了传统室内试验仪器无法测定特定压力下渗透系数的缺陷,不仅可获得各级固结压力下的空隙比,还可得到相应压力下渗透系数。为研究高含水率吹填淤泥的渗透特性,定制环刀高度40mm,内径76.2mm,GDS固结试验系统如图1。

图1 GDS固结试验系统
GDS固结试验原理为在竖向压力p1和反向压力p2作用下对试验土样加压; 在一级固结压力下稳定后,保持竖向压力p1值不变,利用反压p2和底应p3形成的水头差值,开展本级固结压力下的渗透试验。操作原理如图2。
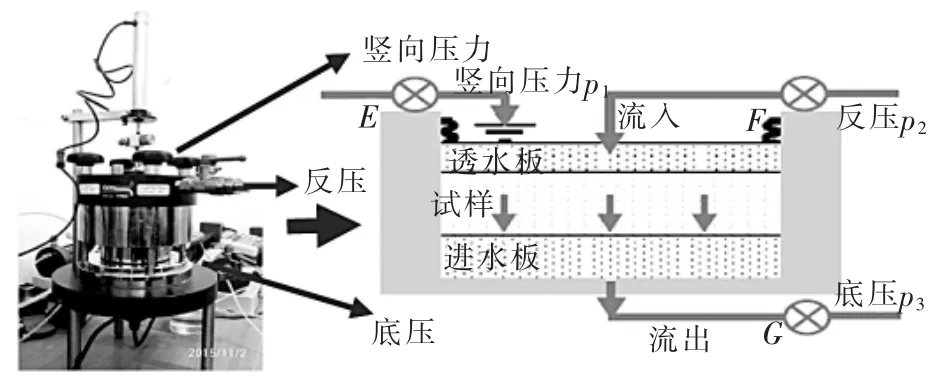
图2 固结—渗透试验原理
2.3 试验及过程
本次试验对3个吹填区的吹填淤泥开展试验。将土样涂抹到环刀中,安装压力室,排出安装过程中内存空气,最后进行试验。试验过程中通过设置不同的p2和p3差值,形成常水头差Δh,开展渗透试验。特定固结压力下,设定多组常水头差Δh,通过试验获得每个水头差下的渗透系数,取平均值后得到特定固结压力下的渗透系数。试验如表2。

表2 试验方案
吹填淤泥固结—渗透试验装样过程、试验过程及试验结束卸载后土样如图3。

图3 试验过程
3 试验结果
3.1 吹填淤泥渗透系数与孔隙比关系
按照表2试验方案,分别对3个吹填区的吹填淤泥开展试验,为直观呈现试验结果,绘制渗透系数kv与固结压力p、孔隙比e之间关系如图4,图5。

图4 渗透系数k v与固结压力p关系
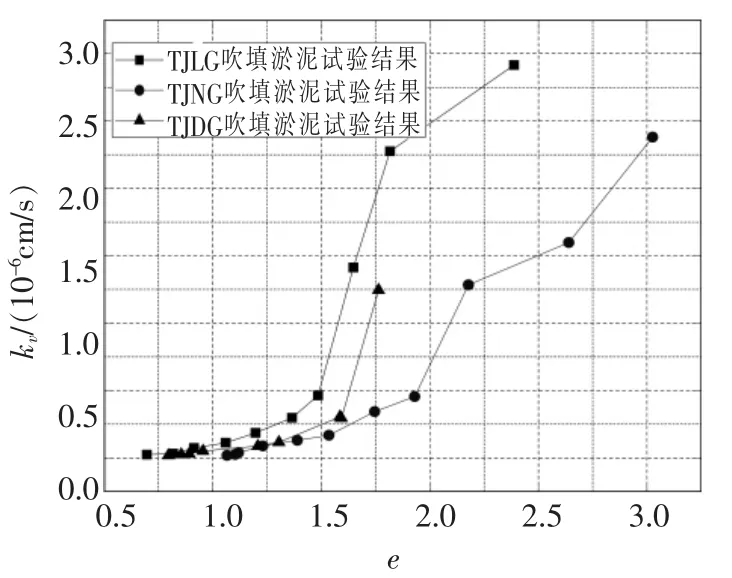
图5 渗透系数kv孔隙比与孔隙比e关系
由图4可看出,渗透系数随着固结压力的增大呈现非线性减小。约以pL=150kPa为分界点,当p<pL时(大应力状态),渗透系数随着固结压力增大减小较快;当p>pL时(小应力状态),渗透系数随着固结压力增大减小不明显。小应力阶段的渗透系数与大应力阶段存在较大差别。
由图5可看出,随着土体被压缩,孔隙比减小,渗透系数随着孔隙比减小呈非线性减小。约以eL=1.5为分界点,当e>eL时,渗透系数随着孔隙比的减小而大幅减小;当e<eL时,渗透系数减小幅度明显降低。在吹填淤泥空隙比变化范围内,渗透系数并不是固定不变的,而是非线性变化的。采用常规理论中假定不变的渗透系数来计算吹填淤泥,与实际情况差别较大。
3.2 非线性渗透模型参数确定及分析
常见适用于软黏土孔隙比与渗透系数的非线性关系有4种:
(1)e-lgkv渗透关系式[15]为e=e0′+Cklgkv。
式中e0′为单位竖向渗透系数对应的孔隙比;Ck为渗透指数。
(2)lge-lgkv渗透关系式[16]为lge=Algkv+B。
式中A,B均为渗透特性参数。
(3)lg[kv(1+e)]-lge模型非线性渗透关系式[17]为lg[kv(1+e)]=lgC+nlge。
式中C为反应土体渗透特性的参考渗透系数(cm/s);n为土体材料参数。
(4)lg(1+e)-lgkv渗透关系式[18]为lg(1+e)=αlgkv+β。
式中α,β均为土性参数。
利用4种渗透关系分别对3种液限吹填淤泥试验结果进行回归拟合,同时用4种关系对不同液限吹填淤泥试验数据进行综合分析,回归拟合曲线如图6。根据拟合曲线确定了天津地区不同液限吹填淤泥4种渗透模型的拟合参数,结果如表3,表4。

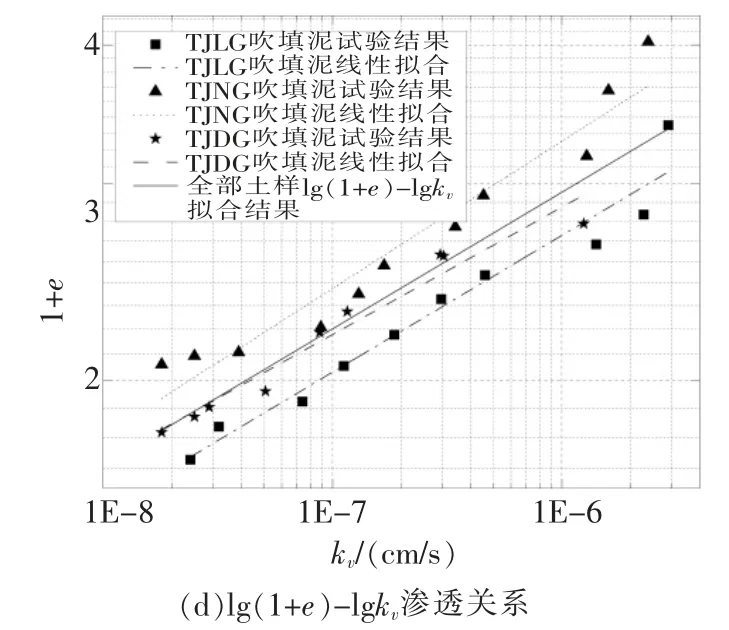
图6 非线性渗透拟合关系
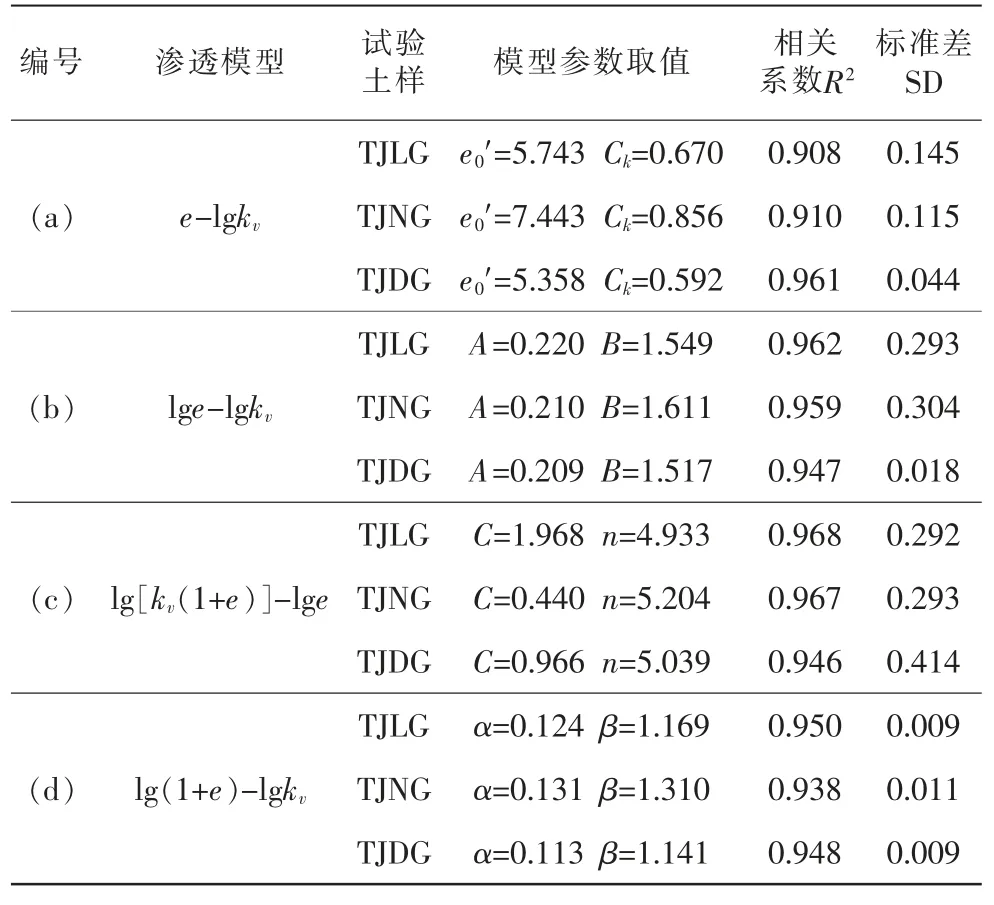
表3 非线性渗透模型拟合参数及相关系数

表4 非线性渗透模型拟合参数及相关系数
由图6可看出,3种液限吹填淤泥渗透试验结果数据点基本散落在拟合曲线的两侧,同时由表3可知,4种非线性渗透模型回归拟合相关系数R2均在0.9以上,拟合标准差SD均较小。从工程应用角度出发,4种非线性渗透模型对不同液限天津吹填淤泥均为试用。
为寻求适用于天津地区吹填淤泥最佳渗透模型,对4种非线性渗透模型拟合参数进行对比分析:对3种液限吹填淤泥而言,e-lgkv模型参数变化范围为Ck=0.592~0.856,e0′=5.358~7.443,变化幅度为1.4~1.5倍;lge-lgkv模型参数变化范围A=0.209~0.220,B=1.517~1.611,相差1.1倍;lg[kv(1+e)]-lge模型参数变化范围C=0.440~1.968,n=4.933~5.204,差值4.5,1.1倍; lg (1+e)-lgkv模型参数变化范围α=0.113~0.131,β=1.310~1.169,相差1.2倍。其中lg[kv(1+e)]-lge模型参数C变化幅度最大,lge-lgkv模型中参数变化范围最小。同时,对比表4中4种模型对不同液限吹填泥综合拟合分析结果可知,lge-lgkv模型拟合相关系数高,拟合标准差小,且模型参数最简单。综合分析,推荐lge-lgkv模型为适用于天津地区吹填淤泥等超软土实际固结变形计算的最佳渗透模型。
4 结语
(1)3种不同液限吹填淤泥kv-e,kv-p 关系表明,软黏土特别是吹填淤泥初始含水量较高、初始孔隙比较大,加固过程中渗透系数随孔隙比的减小和有效应力的增加呈非线性减小,因而按照常规固结理论的基本假定渗透系数为常数不符合实际情况。
(2)采用4种非线性渗透模型对3种液限吹填淤泥kv-e数据进行拟合,获得了模型对应参数。分析表明,从工程应用角度出发,4种常见的非线性渗透模型对天津地区吹填淤泥都是适用的,其中lge-lgkv模型拟合效果最好,且参数最简单,建议将其作为天津地区吹填淤泥等超软土地基实际固结变形计算的最佳非线性渗透模型,且测定的模型参数可直接用于实际工程计算。
