基于有限元法的含蜡原油管道停输过程温降数值模拟
2019-09-05李玉春李中义张弼
李玉春 李中义 张弼
1大庆油田工程有限公司
2广州市市政工程设计研究总院有限公司
3大庆油田有限责任公司第一采油厂
目前国内生产的原油主要是含蜡原油,在生产操作过程中会出现计划停输和事故停输,当原油管道停输时,管内油温开始降低,当停输时间过长时,会发生过度的温度下降,引起凝油层的产生,从而造成凝管事故.由于含蜡原油管道停输对于再启动过程具有重要影响,因此准确掌握停输后含蜡原油管道温度的变化规律,对于突发工况的响应以及再启动计划的制定具有重要的指导意义,同时实现管道安全经济运行.
在停输再启动温降相关研究中,崔慧[1]以管外热流量作为停输再启动过程耦合参量,通过建立非稳态过程传热模型,给出了处理热流量简单、有效的方法.郭兴[2]以三大守恒定律为基础,推导出油流的热力特征线方程,根据管道稳态工况研究管道沿程各点流动参数变化规律.吴海浩[3]研究了重油管道的再启动特性,并应用数值求解方法开发了解决海底稠油管道停输再启动的仿真软件.前人的研究主要集中在原油或稠油管道上,对于含蜡原油管道停输温降模型及有限元法数值求解方面的研究较少.本文根据原油管道正常运行情况,建立停输工况下的传热模型.采用温度场三角形单元格划分→离散→合成有限元这一有限元法求解思路对模型进行数值求解.通过Matlab编制停输计算程序,计算不同停输时间管道的沿程温度,并绘制埋地管道的土壤温度场,分析研究停输过程中温降随时间的变化规律[4],研究结果可为停输再启动工况分析提供理论依据[5-6].
1 构建含蜡原油管输传热数学模型
在管道正常工作条件下,管道中原油的温度远高于周围土壤温度,由于存在较大温差,停输后管道会源源不断地向外传递热量.管道与周围环境之间的温差随着停输时间的增加而减小,热流也逐渐减小.考虑含蜡原油中蜡沉积效应,建立了埋地热油管道、土壤介质、管内介质、大气环境等共同构成的热力系统,如图1所示.

图1 埋地管道物理模型Fig.1 Physical model of buried pipeline
蜡质原油管道在停输后的温度下降过程是一个不稳定的传热过程[7].通过计算,轴向温度梯度远小于径向温度梯度,可以忽略不计,因此三维非稳态传热问题可以简化为管道截面上的二维非稳态问题.
(1)原油的传热方程.其中,液态原油的传热方程为
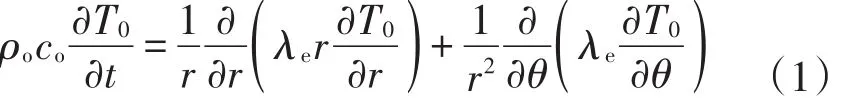
式中:ρo为原油液相密度,kg/m3;co为原油液相比热容,J/(kg.℃);T0为原油液相温度,℃;λe为当量导热系数,W/(m.℃).
引入当量导热系数λe,公式为

凝油层中的传热方程为

式中:ρg为原油固相密度,kg/m3;cg为原油固相比热容,J/(kg.℃);Tg为原油固相温度,℃;λg为原油固相导热系数,W/(m.℃).
(2)保温层的传热方程为
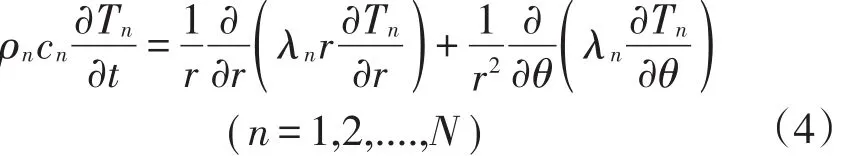
式中:ρn为管道第n层材料密度,kg/m3;cn为管道第n层材料热容,J/(kg.℃).
(3)土壤的传热方程为

式中:ρs为土壤密度,kg/m3;cs为土壤比热容,J/(kg.℃).
2 有限元法数值求解温度场
随着计算机等高科技的快速发展,数值求解已成为解决停输问题的最有效途径之一.目前,对停输问题的解决方案主要采用有限差分法、有限体积法和有限元法.考虑到管道停输温度场计算区域及边界条件的复杂性,本文采用有限元法,其优点是拥有随意布置的网格和节点,对复杂的边界问题求解具有较强的适应性和灵活性[8-9].
2.1 三角形单元格划分
在解决区域温度场的计算中,以管道中心为圆心,由圆弧构成的边界条件是第一类边界条件,地平面构成管道的第三类边界条件[10].边界条件示意图如图2所示.

图2 边界条件示意图Fig.2 Schematic diagram of boundary conditions
为方便求解,有限单元法的网格划分形式采用最为实用的三角单元法.在三角单元法中,每个节点具有相应的数字1、2、....;每一个单元也有自己的编号①、②、…;每个三角形元素顶点用i、j、m逆时针编号.如图3所示,①、②、③等称为内部单元,④、⑦称为边界单元.根据前人总结的经验,取影响深度10 m、宽度20 m的边界为绝热边界.用Matlab软件绘制热影响区三角网格,如图4所示.

图3 温度场区域划分三角形Fig.3 Triangles divided by temperature field region
2.2 温度场的离散
插值函数是一种函数表达式,它使用单元节点值来表示整个单元格值.通过离散方法将三角形元素中任一点(x ,y ) 的温度T值分散到每个单元的三个不同节点.Ti、Tj、Tm用于表示单元中的温度场T,即T=f(Ti,Tj,Tm).该处理方法称为温度场的离散,如图5所示.

图4 热影响区三角单元剖分网格Fig.4 Triangular unit subdivision grid of heat affected zone
对简单三角形,T在每个单元可以近似看做线性分布,表达式为

式中:a1、a2、a3为待定函数,其值由离散的温度场节点温度来确定.
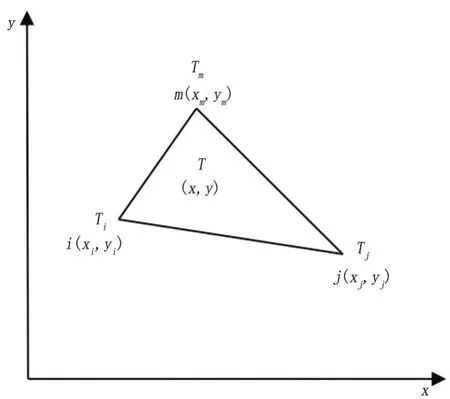
图5 温度离散到三个顶点上Fig.5 Temperature is discretized to three vertices
2.3 合成有限元方程
有限元方法要求最终计算结果是确定计算区域的温度分布,因此有必要对所有分割单元进行整体合成.合成计算基础是

利用有限元方法得到每个节点温度的偏导数并使其等于零,可以得到代数方程
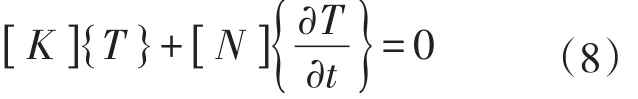
式中:[ K] 为温度刚度矩阵,对称正定矩阵;[ N ]为变温矩阵;{T}为未知温度的列向量.
对公式(8)使用后欧拉法,可得

利用公式(9)可求得各点温度.接下来,基于所建立的含蜡原油管道传热数学模型,结合有限元求解算法,数值求解管道在不同停输时间的温度分布[11].
3 温度场计算
3.1 计算相关参数选取
以国内东北部某含蜡原油输送管道为例,数值求解该管道稳态工况及停输再启动过程[12].所选含蜡原油管道的基本规格、基本物理参数和相关环境温度参数见参考文献[13]~[16].其中,管道外土壤温度场分布的数值模拟结果如图6所示.
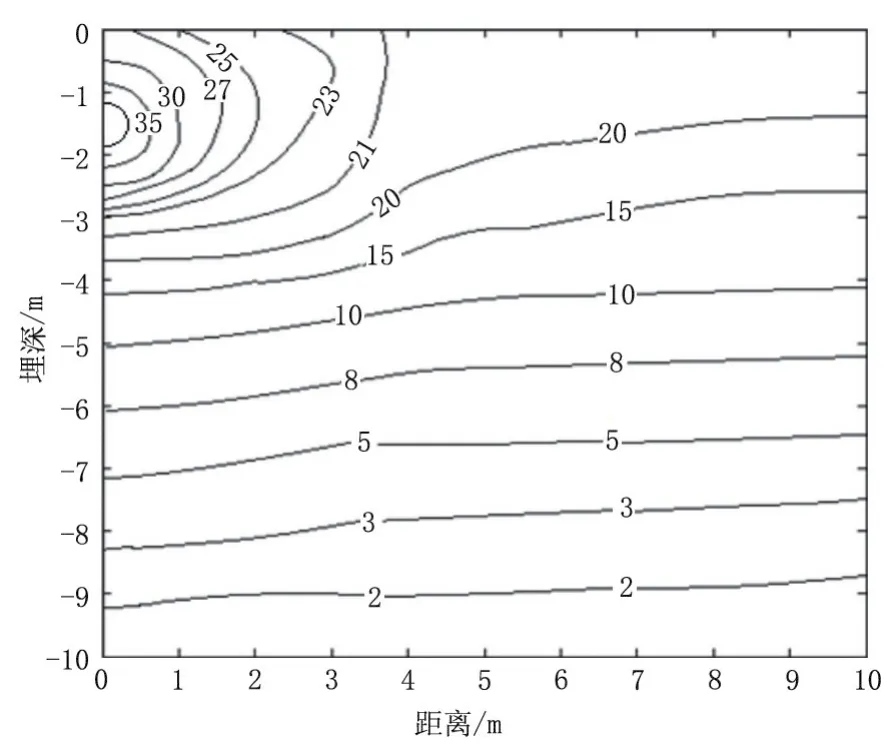
图6 土壤温度场分布图Fig.6 Distribution map of soil temperature field
从图6可以看出,由于管道的散热现象,在距离管道较近处,等温线是一组以管道为中心的偏心圆;离管道越远,管道对周围土壤温度场的影响逐渐减小,当与原油管道距离大于3 m后,等温线近似为一组平行线,土壤温度场受管道热影响较小.
3.2 管道停输温降过程
根据管道基本参数以及所建管道传热模型,数值求解管道沿线温降情况,如图7所示.
根据计算结果,当停输时间为5 h时,管道的入口温度为63.9℃,降低6.1℃,出口温度为51.01℃,降低3.44℃;当停输时间为30 h时,管道入口温度为45.9℃,降低24.1℃,出口温度为37.02℃,降低18.17℃.此外,从图7可以看出,管道中油温高于管道周围的环境温度,随着含蜡原油管道的停输时间增加,油温逐渐降低,油流温度与管道周围环境温度之间的差异较小.随着停输时间的增加,油流温度继续降低并接近环境温度,但温度降低的幅度减小.
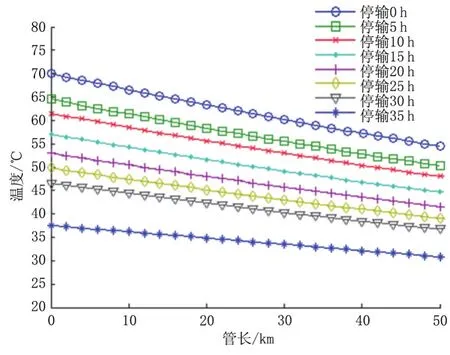
图7 不同停输时间沿程温降Fig.7 Temperature drop along different shutdown time
4 结论
(1)通过对管道温度场计算结果进行分析可知,管道对周围环境温度场的影响随着离管道距离的增大而逐渐减小;在不受热影响的区域外部,温度场等温线近似为一组波动的平行线.
(2)停输后,管道内的油温与管道周围环境存在温差逐渐降低.在停输开始时,管内油流温度较高,原油之间的自然对流作用较大,油温降幅较大.随着管道停输时间的增加,油流温度与管外土壤的温度差逐渐减小,虽然油温依然在降低,但降温幅度越来越小.
(3)基于有限元法的含蜡原油管道停输过程温降数值模拟提供了一种简单易行、准确可靠的温降模拟计算方法.研究成果为含蜡原油停输后再启动过程方案的制定提供了关键数据的获取方法.
