油田注水管网能耗优化控制*

辛胜超 梁永图

中国石油大学(北京)机械与储运工程学院/城市油气输配技术北京市重点实验室

注水开发是油田二次开发的主流手段,注水管网系统一般是由注水站、配水间、注水井口、注水管道以及阀门、弯头等组成的大型复合流体网络系统.在油田注水的研究中,多数学者考虑经济、地质等不确定性因素,以净现值(NPV)最小为目标函数,对注水井的注水率以及注水压力进行研究[1-3].在注水管网优化过程中,往往以最小化管网建设费和运行费为目标函数进行单目标优化,在模型求解中,主要用到启发式算法、数学规划算法,以及人工智能算法.

目前对注水管网的研究不多,国内早期由李从信和陈淼鑫等[4]提出大型油田注水管网的计算和控制方法,后来常玉连等[5]在其基础上提出了注水管网的优化问题.目前的研究是梁永图[6]和张浩然[7]对注水管网的能耗分析模型,其中梁永图主要是研究注水管网MINLP模型的求解方法,提出蚁群算法结合线性近似与单纯形法的混合求解策略,但是智能算法存在稳定性差的缺点,每次求解会有较大的偏差;张浩然分析了注水管网压力流量的敏感性,根据各井的需水流量,反算各管道的初始流量,提出了注水压力流量关系方程--吸水指数方程.

目前供水管网的研究比较成熟[8],与油田注水管网在模型建立以及水力约束等方面存在很多共性.SANKAR等[9]提出了一种非线性模型预测控制(NMPC)技术,可在供水充足和不足的条件下优化配水管网工作状态,使所有需水节点供给量与需求量的累积超额/赤字的平方和偏差最小.所提出的MPC策略在水量过剩时能够满足消费者的需求,同时最小化供应过量水量.在缺水情况下,利用消费者端的存储设施,可减少约20%的日用水赤字.KURIAN等[10]对城市供水管网的优化运行展开研究,在满足供水需求的情况下,把泵和阀门的开关作为控制变量以达到满足供水需求时的最小能量消耗.通过将MINLP分解为三个较小和更简单的子问题并按顺序求解以此加快收敛速度.

1 油田注水系统

注水管网是油田注水系统的主要组成部分,注水系统由注水站、配水间、井口装置及连接的管网组成.水经注水站加压后,通过管网流经配水间,再注入井口,经由注水井将水注入油层.每口注水井都有节流装置,当井口压力过高,则需要进行井口节流来平衡注入压力.目前,油田注水管网多以树状网和环状结合为主.通常在注水范围中心地区布置成环状网,如图1所示;在边沿地区以树状网络形式向四周延伸,如图2所示;在连接点数目较少的地区采用星状网,如图3所示.注水管网中直接和注水站相连的管线称为干线,管径较大,通过干线将水分配到各配水间.直接与配水间、注水井相连的管线称为支线,管径较小,它的作用是从干线取水送到注水井口.从经济上来说,用一条干线接出多条支线费用最省,但从可靠性来讲,以布置几条接近平行的干线为宜,干线与干线之间若有联络线,就形成环状网,当某一根管线损坏,环状网可以通过其他线路给注水井供水,因而供水可靠性较树状网和星状网要高,但相应的建设成本也会增加.

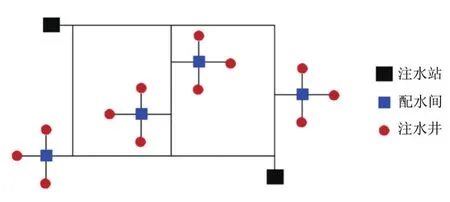
图1 环状注水管网Fig.1 Annular water injection pipe network

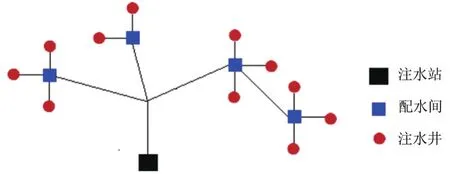
图2 枝状注水管网Fig.2 Branch water injection pipe network

图3 星状注水管网Fig.3 Star water injection pipe network

2 模型建立

2.1 集合描述

在模型中,i∈I,表示注水管网所有节点的集合.其中注水井集合由IW表示,注水站集合由IP表示,IP,IW⊂I;j∈J表示管网中所有管段的集合;k∈Ki表示泵站i的泵运行方案的集合.

2.2 模型假设

(1)注入流体不可压缩,流体的物性参数不随时间、温度、压力等发生变化.

(2)注水管网运行过程为稳态过程,不考虑水击等的影响.

(3)注水泵入口压力设为定值.

2.3 目标函数

目标函数是在满足注入的流量、压力要求以及网络运行压力和流量限制的情况下,计算出注水管网运行方案使能耗最小.具体目标函数为

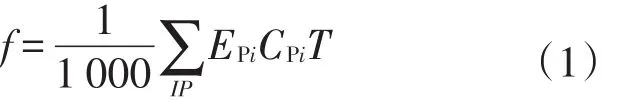
式中:EPi为泵的运行功率,W;CPi为泵的费用系数,元/(kWh);T为运行时长,h.

3 约束条件

3.1 泵站约束

HBPi,k为二元变量,当HBPi,k=1时,节点i为泵站,运行第k个开泵方案,提供的压力为pi;当HBPi,k=0时,节点i不为泵站,不提供压能.数学表达式为

其中:ρ为液体密度;g取9.8,m/s2;ai,k、bi,k为泵送扬程线性化参数;QSi为流量,m3/s;m取0.25;M表示极大值(取109).

公式(4)表示如果节点i是泵站,则必须运行一个开泵方案.

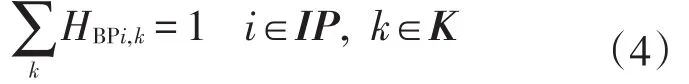
当HBPi,k=1时,节点i为泵站,运行第k个开泵方案,泵的输出功率为EPi,在满足进泵流量区间内,泵在高效区工作,本模型将泵效率视为定值1.数学表达式为

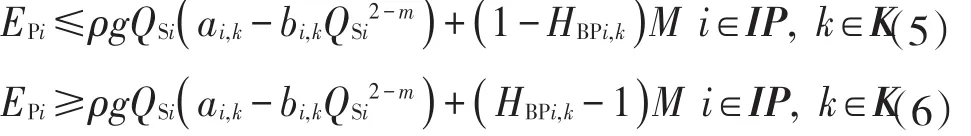
当HBPi,k=1时,节点i为泵站,运行第k个开泵方案,进入泵站i的流量QSi必须在[QQBmini,k,QQBmaxi,k]之内.数学表达为

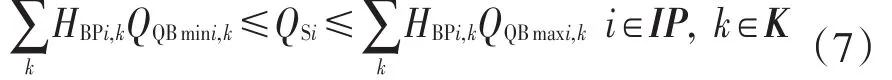
3.2 管段约束

管段的摩擦阻力通过海曾威廉公式计算.pMj为第j个管段的摩擦阻力,Pa,QGDj表示第j个管段的流量,m3/s;Lj表示第j个管段的长度,m;C为摩擦阻力计算参数,取100;dj表示第j个管段的管径,m.计算公式为

第 j个管段的流量QGDj必须满足流量范围[-QGDmaxj,QGDmaxj]的要求,即

FQZj、FQFj均为二元变量,当FQZj=1时,管段流量为正;当FQFj=1时,管段流量为负;当FQFj=0或者FQZj=0时,管段流量不受约束,M表示一个极大值,具体约束如下

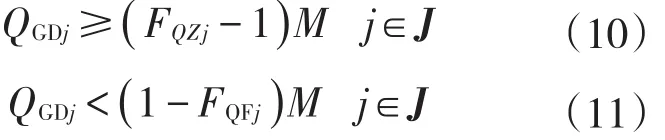
管段流量只能是正或者是负,具体表达形式为

当FQZj=1时,管段的流量为正,管段的实际摩擦阻力损失pFj等于摩擦阻力损失的绝对值pMj.数学表达式为

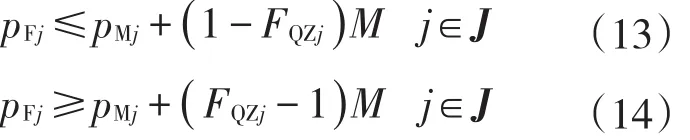
当FQFj=1时,管段的流量为负,管段的实际摩擦阻力损失PFj等于摩擦阻力损失的绝对值PMj的相反数.数学表达式为

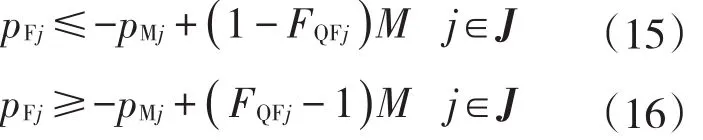
BSi,j、BNi,j为二元变量.当BSi,j=1表示当节点i是管段j的起点,BNi,j=1表示节点i是管段j的终点时,管段j的摩擦阻力损失等于两个节点之间的压差.具体约束形式为

BPi、BWi为二元变量.BNi,j=1时,节点i为管段的终点,节点的流入量为管段的流量QGDj;BPi=1时,节点i为泵站,节点的流入量为泵的注入量QSi,排出流量为管段的流量QGDj.根据定义,BWi=1时,该节点为注水井,该节点的流出流量为该井的实际注入流量QPi,该节点的流入量为管段的流量QGDj.具体约束形式为

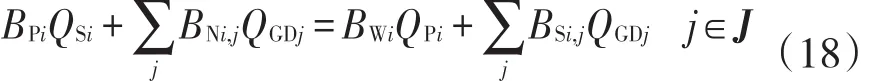
当BWi=1时,节点i为注水井,由于井口前有节流装置,因此阀门前压力pi与井内注入压力pWi

之差等于节流压力降pJi.具体数学表达式为

节点i的压力pi应满足管网系统限制范围[pmin,pmax],即

3.3 注水井约束

当节点i为注水井时,实际注水流量QPi必须在流量要求范围[QWmini,QWmaxi]之内.约束形式如下

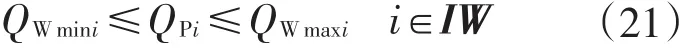
当节点i为注水井时,注入压力pWi应满足注入压力范围[pWmini,pWmaxi]要求.约束形式如下

当节点i为注水井时,井口压力pWi和井的注入流量QPi需要满足吸水指数方程的约束,αi、βi为吸水指数方程系数.具体数学表达式如下

3.4 线性化

由于流量与压力的非线性关系,数学模型为MINLP模型,采用分段线性化方法使模型成为MILP模型,便于求解.方程式(2)和(3)替换为方程式(24)~(29),方程式(5)和(6)替换为方程式(30)和(31),方程式(8)替换为方程式(32)~(36).

ρ 为液体密度,ai,k、bi,k、ma、na为泵送扬程线性化参数.当HBi,k,a=1即节点i为泵站并且流量范围处于a区间、运行第k种开泵方案时,节点i的压力为第k种启泵方案提供的扬程.数学表达式如下

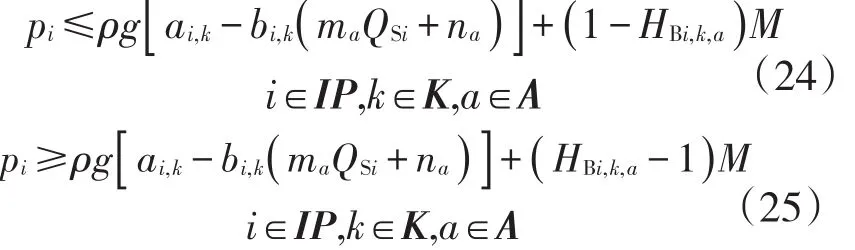
若节点i为泵站,则其流量范围必处于一个区间,必须运行一种启泵方案,具体约束形式如下

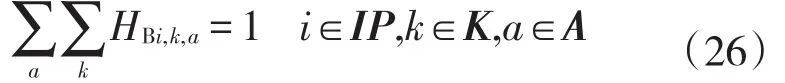
泵注入流量QSi必须满足注入流量区间范围[QAmina,QAmaxa],具体约束形式为

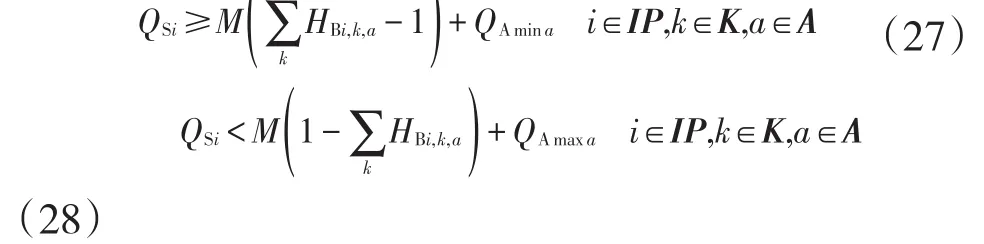
当i节点(i为泵站)选择第k种启泵方案,即HBPi,k=1时,其过泵流量必处于一个流量区间范围内,具体约束形式为

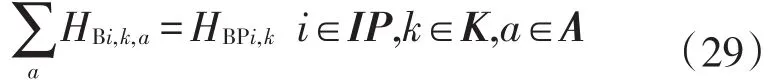
ai,k、bi,k、wa、ua为泵送功率线性化参数.节点i为泵站并且流量范围处于a区间、运行第k种开泵方案时,输出的功率表达式为

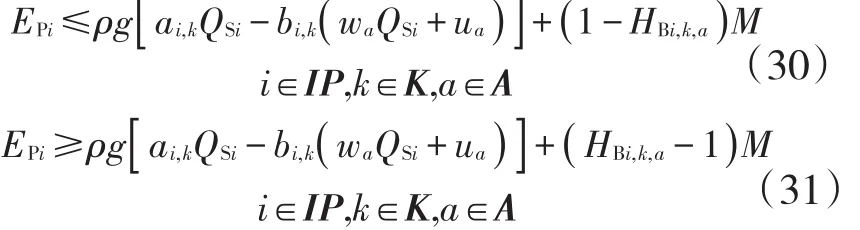
zn、rn为线性化系数,若管段j流量范围处于n区间,即FGDj,n=1,管段j的沿程摩阻绝对值用海增威廉公式计算.数学表达式为

管段j的流量必处于一个流量区间.

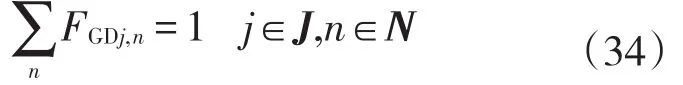
当管段j流量QGDj处于n区间时,必须满足流量区间范围[QNminn,QNmaxn].数学表达式为

4 模型求解与结果分析

4.1 模型分段线性化

原模型为MINLP模型,求解困难,通过分段线性化的方法在保证求解精度的前提下简化与流量有关的摩擦阻力项、泵扬程和功率项,从而将非线性难求解的问题转化为线性问题,MINLP模型转化为MILP模型.在分段线性化中,将原非线性函数按自变量的值分为若干连续区间,然后用一个线性函数拟合每个区间的非线性曲线,使整个非线性函数可以用一系列线性函数代替.分段线性化如图4、图5、图6所示.纵轴代表原始非线性函数,横轴代表自变量,不同颜色的曲线表示划分的区间,并列出相应的线性函数.

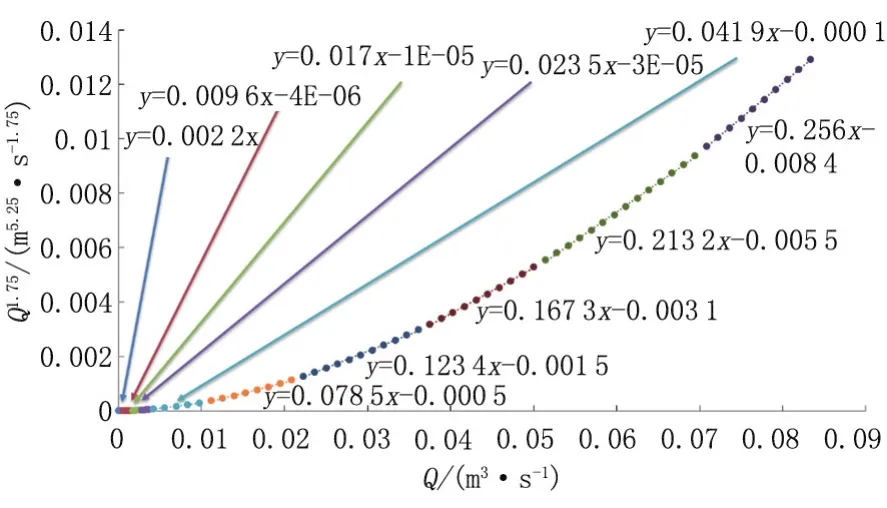
图4 与Q1.75相关的泵扬程分段线性化Fig.4 Piecewise linearization of pump head associated withQ1.75

4.2 结果分析讨论

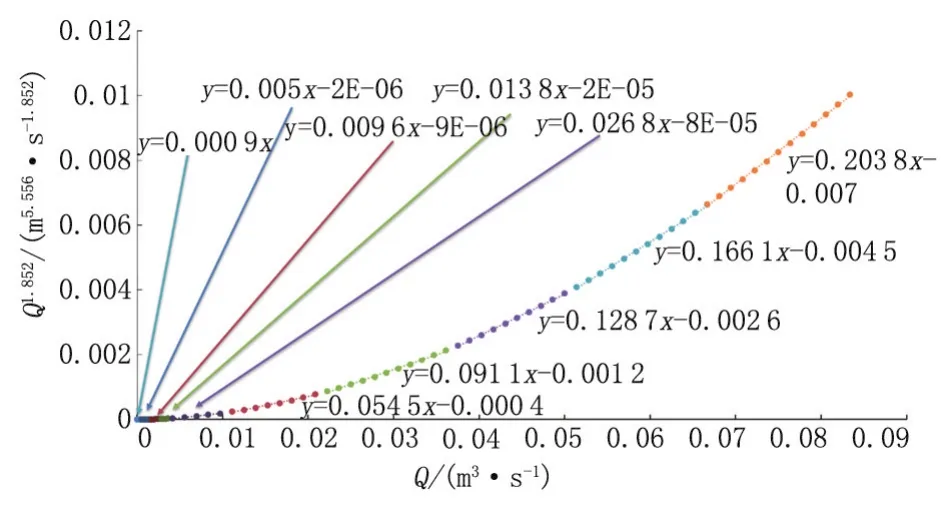
图5 与Q1.852相关的管路摩阻分段线性化Fig.5 Piecewise linearization of pipeline friction loss associated withQ1.852

图6 与Q2.75相关的泵功率分段线性化Fig.6 Piecewise linearization of pump power associated withQ2.75

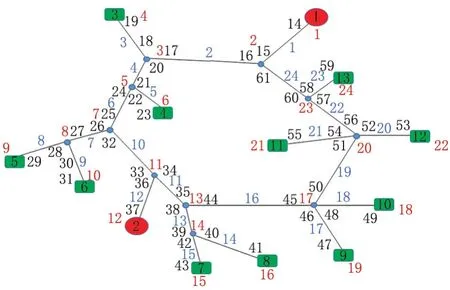
图7 注水管网拓扑结构图Fig.7 Topological structure of water injection pipe network

注水管网图谱结构如图7所示,由2个注水站(红色椭圆1和2)、11个注水井(绿色框图3~13)、24个汇点(红色数字1~24)、24个管段(蓝色数字1~24)、61个节点(黑色数字1~61)组成.属于中型结构的环枝状管网,通过分段线性化的方法把模型中的非线性项转化为线性项,从而变为MILP模型,采用Matlab与Gurobi耦合求解,所得结果如表1所示.

通过Matlab与Gurobi联合调用,耗时18.06 s,求出该注水管网最小运行费用为247 841.4元,两注水泵站均采取第二种开泵方案.图8表示注水管网各管段的流量.图9和图10表示注水井实际注水量与需求量的偏差程度,在11口注水井中,第一口井(编号3)注水量偏差最大为13.9%,且只有

表1 泵运行参数Tab.1 Operating parameters of pump

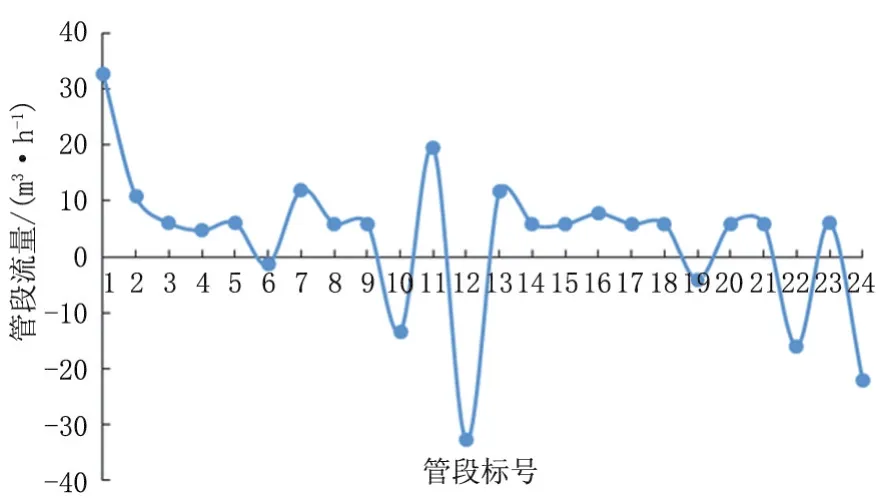
图8 注水管网流量图Fig.8 Flowrate diagram of water injection pipe network

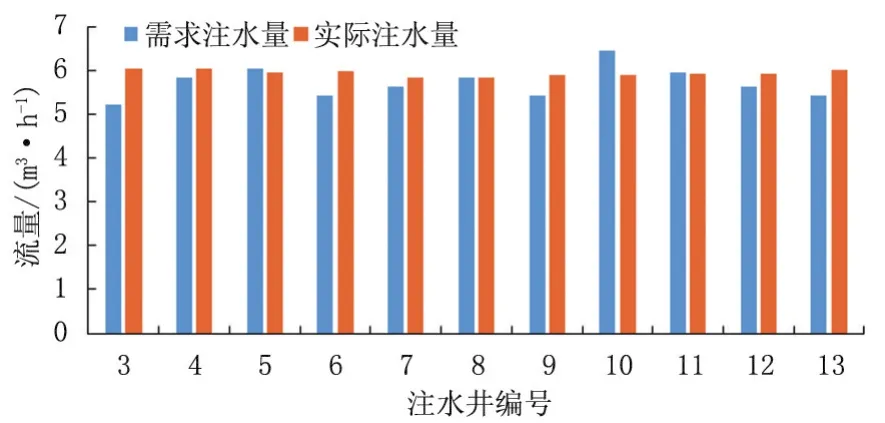
图9 注水井注入量与需求量Fig.9 Injection and demand volume of waterinjection wells

图10 注水井注入量偏差Fig.0 Injection volume deviation of water injection wells

该注水井注水量偏差超过10%,其余10口注水井水量偏差均小于10%,61.5%的注水井偏差在5%以下,标号为8的注水井注水量偏差最小为0.图11表示管网的运行压力约为16 MPa左右.图12为注水井口的节流压力降,节流压降在0.1~0.3 MPa之间.如图13所示管段压降均在0.04 MPa以下.

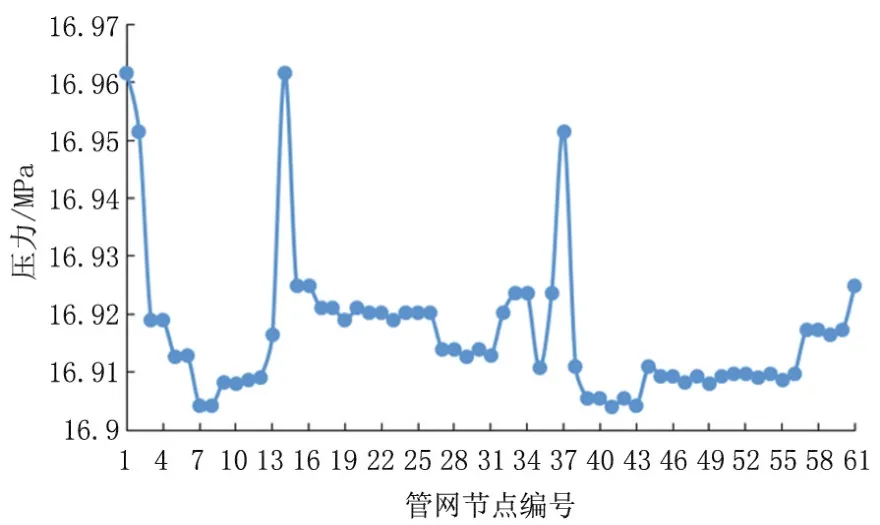
图11 注水管网节点压力Fig.11 Node pressure of water injection pipe network

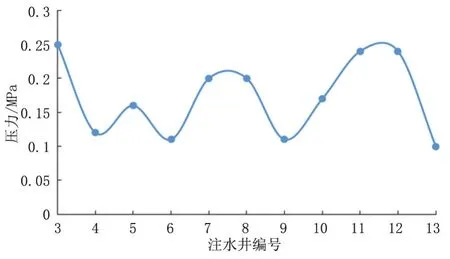
图12 注水井口节流压力降Fig.12 Throttling pressure drop of water injection wells

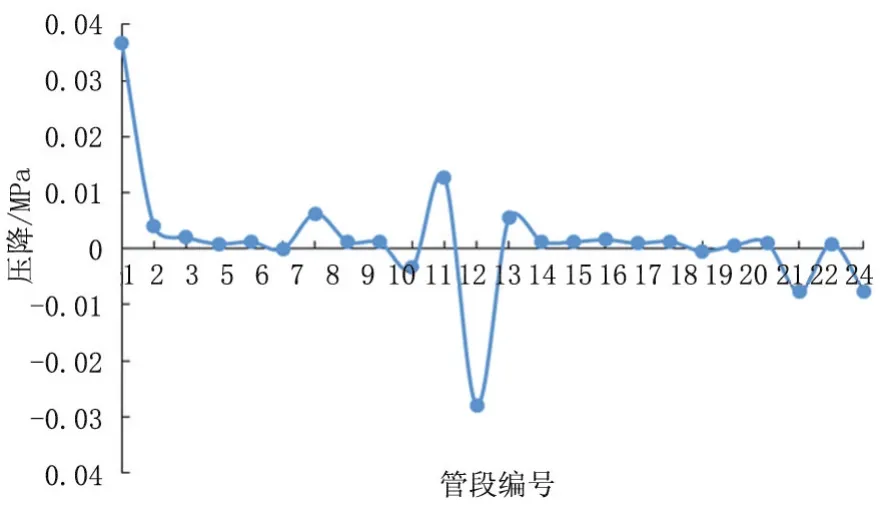
图13 注水管网压降Fig.13 Pressure dropof water injection pipe network

由结果可知,在满足管网运行能耗最低的情况下,求解得到的注水量偏差在可接受范围之内,验证了该模型在油田注水管网节能降耗的实用性.在今后的研究中,可将注水量偏差与管网可靠性纳为目标函数,进行注水管网多目标优化.

5 结论

(1)针对油田注水管网提出的MINLP模型,采用分段线性化变为MILP模型可简化求解,注水算例验证了模型在油田节能降耗应用中的可行性.

(2)通过实例分析,在给出油田最优开泵方案达到最低能耗的同时,90.9%的注水井注水量偏差小于10%,61.5%的注水井偏差在5%以下,注水量偏差在可接受范围之内.