县域养殖池塘景观格局指数的粒度效应——以江苏省兴化市为例

谢 奎，程家骅，张寒野*

(1. 中国水产科学研究院东海水产研究所,农业农村部东海渔业资源开发利用重点实验室,上海 200090； 2. 上海海洋大学海洋科学学院,上海 201306)

景观格局分析主要是研究景观要素的类型、形状、规模等在空间上的分布与配置，既是景观异质性的具体体现，也是各种生态过程在不同尺度上作用的结果[1]。近年来，国内外学者针对景观格局做了大量的研究工作，不仅涉及自然因素对景观格局的作用[2-3]，也更加注重研究人类活动对景观格局的影响[4-6]。景观格局有2种常用的度量方法：景观格局指数法与地统计学方法。其中，景观格局指数以能够高度浓缩景观信息，反映其结构组成与空间配置状况的优势，因此得以广泛应用[7]。但作为分析景观格局特征的定量化指标，景观格局指数通常以栅格数据为数据源，基于栅格单元(研究范围内最小的空间单元，尺度意义上的粒度)进行相关指标的计算，这样就导致了“可塑性面积单元问题”[8]。在进行面积数据(例如遥感影像数据、土地利用数据等)的分析时，由于面积单元(栅格细胞或粒度)定义的不同，计算结果会发生相应变化，产生明显的尺度依赖性。因此，为了确保选取的栅格单元能够准确有效地反映研究区域的景观格局特征，既能够对空间信息的冗余噪声产生很好的抑制作用，同时还可以避免丢失有效信息，从而保证景观格局分析的合理性，在计算相关指标之前，需要结合研究区域及数据资料选择适宜的分析尺度[9]。

尺度通常用空间和时间上的幅度(extent)与粒度(grain)来描述[10]，当研究区域和时间一定时，空间上的幅度和时间上的幅度与粒度也随之确定，此时仅需对空间粒度进行研究[11]。很多学者的研究已经证明了景观格局指数普遍存在尺度依赖性[12-14]。例如，杨丽等[12]分析了泾河流域30～200 m粒度范围内的景观格局指数的粒度效应；赵文武等[13]分析了陕北延河流域不同比例尺条件下的景观格局指数的粒度变化效应；张玲玲等[14]分析了沂蒙山区不同空间幅度的景观格局指数的粒度效应。但前人的研究成果也同样说明：不同景观的格局特征不一样，对于尺度变化的响应也不相同，只有基于特定尺度对研究区域景观进行研究，才能准确地揭示景观格局特征。因此，只存在适用于特定景观格局分析的适宜分析尺度，没有普遍适用的最佳尺度[15]。而且国内外学者对景观格局指数的粒度效应大多都是从研究区域景观整体水平的角度进行分析，针对某一种斑块类型景观指数的粒度效应研究尚不多见。因此，通过以江苏省兴化市水产养殖池塘景观为研究对象，以天绘一号遥感影像为数据源，提取兴化市水产养殖池塘空间数据。基于生态学理论，在斑块类型水平上选取了11个常用的景观格局指数，通过计算各个景观格局指数在不同粒度上的数值，探究兴化市养殖池塘景观格局的粒度效应问题，确定兴化市水产养殖池塘景观指数的适宜空间粒度。

1 材料与方法

1.1 研究区域概况

兴化市(32°44′N～33°16′N、119°43′E～120°16′E)位于江苏省泰州市的北部，地处江淮之间，里下河地区腹地；属于北亚热带湿润季风气候，具有四季分明、雨量充沛、冬寒夏热和雨热同步等特点；下辖3个街道、26个镇、4个乡、1个省级经济开发区；全市总面积2 393.35 km2，境内河道纵横，湖荡棋布，水域面积达800 km2。

1.2 数据来源与处理

研究数据包括遥感数据与辅助数据2个部分。其中，遥感数据为2012年天绘一号遥感卫星2 m全色影像和10 m多光谱影像数据；辅助数据主要用于遥感影像的解译与分类，包括研究区域的行政区划矢量数据、水产养殖统计数据及Google Earth影像图数据。

利用ENVI 5.1对遥感影像进行辐射定标、大气校正、几何校正、镶嵌和裁剪等预处理，生成研究区域影像。为了保证解译结果准确可靠，开展了研究区域野外实地考察，建立目视解译标志和标准。在ArcGIS 10.2的支持下，采用传统的人工目视解译方法，依据规定判别法则对遥感影像进行信息提取。通过Google Earth高清遥感影像等辅助数据对初步解译结果进行修正，并结合实地GPS测量数据校验遥感监测数据，结果能够满足实验需求。最后，通过格式转换、空间叠加等处理，进行数据统计分析，获得兴化市水产养殖池塘空间分布矢量数据。

1.3 研究方法

利用ArcGIS 10.2中的空间分析模块(spatial analysis)，参照前人的研究经验[16]，采用中心属性法将解译出的兴化市水产养殖池塘空间分布图的矢量数据栅格化，转化为以10 m为间隔的10～200 m粒度范围的栅格数据。

景观格局指数通常划分为3个层次：斑块水平、斑块类型、景观水平。斑块水平反映研究区域内单个斑块的结构特征，是计算其他景观级别指标的基础；斑块类型反映研究区域内的结构特征；景观水平反映研究区域内整体的特征[17]。由于是对研究区域内水产养殖池塘景观格局指数的粒度效应进行分析，因此参照国内外学者对景观格局指数选取的相关研究成果[18-21]，以及研究区域水产养殖池塘景观特征，在斑块类型上选择景观面积(class area，CA)、斑块个数(number of patches，NP)、斑块密度(patch density，PD)、最大斑块指数(largest patch index，LPI)、平均斑块面积(mean patch size，MPS)、平均近邻指数(mean proximity index，MPI)、平均最近距离(mean nearest-neighbor distance，MNN)、相似毗邻百分比(percentage of like adjacency，PLADJ)、斑块结合指数(patch cohesion index，COHESION)、聚集度指数(aggregation index，AI)、分离度指数(landscape isolation，FI)11个景观格局指数，利用Fragstats 4.2软件计算景观格局指数，然后将结果导入到Excel中，以不同粒度为横轴，以该粒度下对应的景观格局指数为纵轴，建立兴化市水产养殖池塘景观格局指数的粒度效应曲线，分析兴化市水产养殖池塘景观格局指数随粒度变化的规律，从而确定研究区域的适宜分析粒度。各景观格局指数的计算公式及生态学意义参见文献[22-24]。

2 结果与分析

2.1 水产养殖池塘景观格局指数的粒度效应

根据Fragstats 4.2软件计算的景观格局指数结果，绘制兴化市水产养殖池塘景观格局指数的粒度响应曲线(图1)。

从图1可以看出，随着空间粒度的粗化，兴化市水产养殖池塘景观格局指数呈现出不同的变化趋势，表明空间粒度对景观格局指数具有明显的影响，即随着粒度变粗，斑块边界发生改变，斑块分割或融合，导致景观格局的有关特征发生相应的改变，从而使景观格局指数也产生相应变化。当粒度增加到一定程度时产生突变，出现明显或不明显的尺度转折点。同时，由于不同景观格局指数是景观格局特征各个方面信息的表征，因此其尺度转折点的位置并不相同。

根据景观格局指数对空间粒度的响应和粒度效应关系，大体上将上述景观格局指数的粒度效应归为4类：

1)随粒度粗化，景观格局指数响应曲线呈现出单调递增趋势，不具有尺度转折点，粒度效应关系比较明确。代表性指数为平均最近距离。平均最近距离采用各斑块与周围最近斑块之间距离的平均数进行计算，随着粒度的增加，斑块之间发生合并，小的斑块被融合，斑块形状发生改变，但平均数却不会发生剧烈的波动。

2)随粒度粗化，景观格局指数响应曲线整体呈现出非单调上升或下降趋势，具有尺度转折点。具体指数包括斑块个数、斑块密度、平均斑块面积、相似毗邻百分比、聚集度指数及分离度指数。斑块个数与斑块密度的变化规律比较相似，在10～20 m的粒度范围内，其指数值随着粒度增加呈快速降低的趋势；当粒度继续增加时，降速趋于缓和。总体来看，斑块个数和斑块密度对空间粒度的变化响应比较敏感，尤其是当粒度较小时，斑块个数会随粒度变粗而快速减少，反映了研究区域养殖池塘景观中小面积养殖池塘斑块所占比例较多，当粒度粗化时，小的斑块发生融合。相似毗邻百分比与聚集度指数的粒度效应曲线非常类似，在粒度的增加初期，景观格局指数值持续降低，到190 m空间粒度之后出现上升的趋势，尺度转折点均出现在20 m与190 m处。分离度指数反映了景观中养殖池塘斑块个体的离散度随粒度变粗而降低，其原因主要是由于在粒度变粗过程中，小的养殖池塘斑块和养殖池塘总斑块的数量在减少，导致分离度指数降低。

3)随粒度粗化，景观格局指数响应曲线呈现出波浪式下降趋势，具有明显的尺度转折点。具体指数包括平均近邻指数、斑块结合指数。斑块结合指数与平均近邻指数随着粒度变粗呈现出波浪式下降的变化趋势，出现明显的尺度转折点，且尺度转折点的数量相对较多。

4)随粒度粗化，景观格局指数响应曲线呈现出无规律的变化，具有显著的尺度转折点。具体指数包括景观面积与最大斑块指数。这2个指数随着粒度的增加，粒度效应曲线比较复杂，尺度区间非常显著。

2.2 水产养殖池塘景观格局指数粒度效应的变异特征

景观格局指数对空间粒度变化的敏感性程度可以用景观格局指数随粒度粗化的变异系数来表示。由表1可知，随着空间粒度的粗化，各景观格局指数的变异系数均呈现出不同程度的变化。根据变异系数(coefficient of variation，CV)的大小，将敏感性程度分为3种：不敏感(CV<0.1)；一般敏感(0.1≤CV<0.5)；较敏感(CV≥0.5)。其中不敏感的景观格局指数包括：景观面积、斑块结合指数，其中景观面积的变异系数最小，为0.003 0，说明粒度的粗化对景观面积的影响最小；一般敏感的景观格局指数包括：最大斑块指数、相似毗邻百分比、斑块结合指数、聚集度指数、分离度指数，其中斑块结合指数的变异系数最小，为0.034 8；较为敏感的景观格局指数包括：斑块个数、斑块密度、平均斑块面积、平均近邻指数，其中斑块个数的变异系数最大，为 0.828 4，表明随着粒度的粗化，斑块个数受到的影响最大。

图1 水产养殖池塘景观格局指数的粒度效应曲线Fig.1 Grain size effect curve of landscape pattern index of aquaculture ponds

景观格局指数平均值标准差最小值最大值变异系数景观面积/hm2 CA37.644 10.114 537.371 037.821 00.003 0斑块个数/个 NP5 414.350 04 485.478 3168 0.000 018 842.000 00.828 4斑块密度/(个·100 hm-2)PD14.373 111.892 84.466 649.964 70.827 4最大斑块指数/% LPI4.712 12.040 30.677 97.699 80.433 0平均斑块面积/hm2 MPS10.898 76.205 02.001 422.388 30.569 3平均近邻指数MPI26.170 117.622 39.563 973.250 70.673 4平均最近距离/m MNN288.744 4144.681 850.774 9523.669 50.501 1相似毗邻百分比/% PLADJ55.686 512.564 042.124 584.980 10.225 6斑块结合指数/% COHESION89.201 63.099 984.188 893.883 50.034 8聚集度指数/% AI55.970 112.451 442.555 485.045 80.222 5分离度指数FI0.448 20.171 60.266 90.891 40.382 8

2.3 数学模型拟合

通过上述的分析可知，研究区域大部分景观格局指数对粒度变化的响应较为明显，并且变化的趋势呈现出一定的线性或非线性特征，能够用数学模型对景观格局指数随粒度变化的响应曲线进行模拟(表2)。

由表2可知，除景观面积外，其他10个指数的拟合效果均达到显著和极显著水平，说明这些指数对尺度变化的响应均具有较为明显的规律性，可通过拟合方程对其变化进行精确地预测，即空间粒度与景观格局指数之间确实存在相关关系，具有较强的可预测性。其中平均最近距离可以用一元线性函数进行拟合，且拟合度最高，达到了0.999 2；斑块个数与斑块密度可用三次多项式进行拟合，且拟合度相同，均为0.982 7。最大斑块指数可用幂函数进行拟合，拟合函数虽然达到了极显著水平，可是其决定系数相对较低，仅为0.791 2，可能与养殖池塘的空间分布方式有关，仅具有一定的可预测性。而景观面积的拟合度仅为0.159 1，拟合效果较差，具体原因可能是人工选取的粒度不合适，或是随着粒度变粗导致误差增大，也可能是这个指数本身的特殊性或无规律性。其所建立的一元线性回归方程式无意义，不具备可预测性。

表2 景观格局指数粒度响应的拟合函数Tab.2 Fitting function of grain size response of landscape pattern index

注：**代表拟合效果非常显著

Note:**represents that the fitting effect is very significant

2.4 适宜空间粒度的确定

基于不同尺度下的景观格局分析结果会有所不同，因此确定适宜的空间粒度对于景观格局的研究尤其重要。景观格局指数随粒度变化的第一尺度域可用来确定粒度大小及景观格局分析的适宜粒度范围，通常根据第一尺度转折点确定[13]。根据研究区域各景观格局指数随粒度变化响应曲线的拐点与跃变区间，确定兴化市养殖池塘景观格局分析中的第一尺度域和适宜粒度范围(表3)。

不同景观格局指数反映景观特征的不同方面，由表3可知，研究区域景观格局指数具有尺度转折点，代表景观特征会在尺度转折点处发生较大的变化。而且由于景观格局指数尺度转折点的位置并不一致，导致景观整体特征的尺度转折点是一个区间，而非一个固定数值。在这个区间内，景观格局指数值发生跃变现象。由表1可以看出，绝大多数景观格局指数随粒度变化的响应曲线存在显著拐点或跃变区间，并且本研究所选取景观格局指数的第一尺度域多集中在10～20 m。在粒度选择时，为了确保计算的质量、反映景观格局的总体特征信息，同时又可以使计算过程中的工作量不至于过大，应该在第一尺度域内选择中等偏大的粒度作为适宜的粒度[25]。因此，通过对各景观格局指数第一尺度域的综合考虑，该研究区域水产养殖池塘景观的最佳尺度范围为15～20 m，确定20 m为适宜空间粒度。

3 结论与讨论

3.1 结论

空间粒度变化的研究，对于景观格局指数的计算非常必要。本研究以兴化市水产养殖池塘为研究对象，对11个景观格局指数的粒度效应进行了探讨，得出如下结论：

(1)通过线性回归分析可知，研究区域水产养殖池塘景观格局指数的粒度效应较为显著。随粒度的变粗，不同景观格局指数呈现出不同的变化趋势。除了平均最近距离随粒度变粗单调递增，没有尺度转折点外，其余10个景观格局指数随着粒度的变粗具有非单调的变化趋势，具有明显或不明显的尺度转折点。

(2)不同景观对象的空间格局分析，选择适宜的尺度进行景观格局特征及其变化分析尤为重要。粒度大小以及景观格局分析适宜取值范围的确定，需要根据景观格局指数随粒度变化的第一尺度域进行，该研究区域水产养殖池塘景观的最佳尺度范围为15～20 m，确定20 m为适宜空间粒度。

(3)在本研究所选的11个景观格局指数中，其中景观面积的拟合度较低，可能是由于粒度选取不合适或指数本身的特殊性等原因造成。其余10个景观格局指数的变化趋势均能够进行较好的拟合，说明空间粒度与景观格局指数具有相关性。

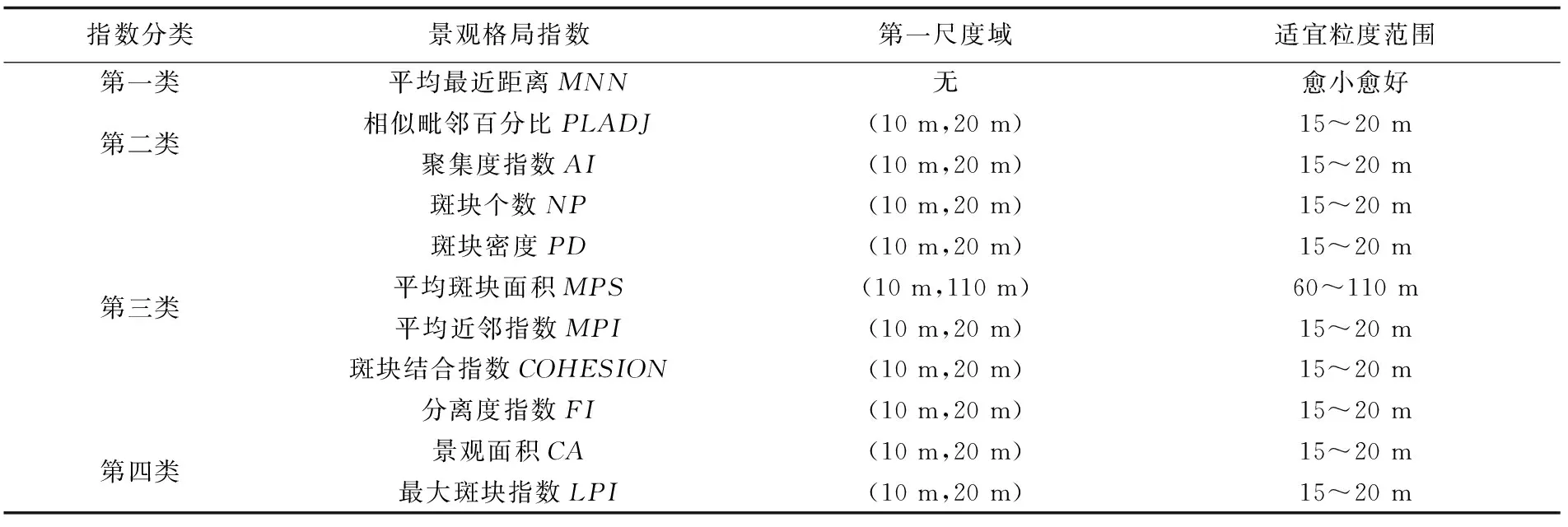
表3 景观格局指数适宜粒度范围Tab.3 Appropriate size range of landscape pattern index

3.2 讨论

(1)景观生态学中尺度问题的重要性已被许多学者充分认识到，并进行了大量的研究，但对于适宜分析粒度如何进行选择，还未形成完整的理论与方法体系。如果使用不同的数据对同一研究区域进行分析，那么适宜分析粒度可能会不一致，分析结果也可能会有所不同。因此本研究得出的适宜空间粒度不一定适用于其他研究区域。因此，对于适宜空间粒度的确定要基于研究区的实际情况进行分析。

(2)在进行景观格局指数分析时，由于目前的景观格局指数众多，会遗漏一些能够更好反映研究区域景观格局特征的指标。对于指数的选取以及粒度的划分受主观因素影响较大。在进行尺度综合选取时，由于拐点并不一致，也只能参照大概的范围进行人为选定。需要进一步研究如何减少主观因素，降低人为划分对景观格局内在规律性的影响。

(3)景观格局指数不仅受空间粒度的影响，同样还受幅度的影响，在下一步工作中，将考虑如何将粒度与幅度相结合，研究不同幅度区域间景观格局指数的尺度效应，从而进行不同区域间的景观格局对比研究。