一种基于DNA折纸系统求解最大团问题的模型

严洋洋，殷志祥*，崔建中,b，唐 震

（安徽理工大学 a.数学与大数据学院；b.电气与信息工程学院，安徽 淮南 232001）

由于DNA分子具有良好的可编程性，可利用它的双螺旋结构和碱基互补配对原则可以将其折叠成不同形状、不同尺寸的DNA纳米材料[1]。

早在1982年，Seeman就提出了利用DNA分子创建不同简单结构的想法和DNA纳米材料的概念。即利用碱基互补配对的原则和生物技术合成任意序列的DNA片段的能力，构造出不同的纳米结构，随之，他构造了许多分支型的复合体，如DX、TX、PX等，并将其应用到四面体、八面体等纳米结构的自组装中[2]。此后，出现了越来越多的不同形状、不同尺寸的二维DNA自组装体。如Yan[3]设计了四条手臂的交叉体、He[4]构造的二维阵列。

1 相关研究

2006年，Pauw提出了一种由DNA构建空间结构的新方法DNA折纸术[5]。它是一种具有里程碑性的全新的DNA自组装方法，能够很容易得构造出更复杂、更多样的DNA自组装体。与传统的交叉策略的DNA自组装不同，DNA折纸是将一条长的单的DNA链（脚手架链）在一些预设的短的DNA链（订书钉链）指导下，利用DNA分子碱基互补配对的原则，构造出不同形状、不同尺寸纳米结构，如笑脸、三角形、星型等[6]。对比使用传统的自主装方法构造出的纳米结构，其优点在于构造出的纳米结构更稳定、更复杂、更具有可控性及寻址性。此后，DNA折纸进入了快速发展时期，渐渐地拓展到三维空间。

近十年的研究成果表明，DNA折纸已经越来越强大了[7-15]。由DNA分子创建的纳米结构越来越多样化、复杂化，但其目标绝不是将其设计成各种各样的结构，而更多的是让它们“动”起来[16-18]。不仅如此，随着DNA折纸的发展，许多应用也得以实现，如药物传送[19-20]、纳米机器人[21-22]等。

最大团问题（maximum clique problem）是一个十分经典的 NP（non-deterministic polynomial）完全问题，也是图论的一个十分重要的研究分支。在很多方面都有着举足轻重的应用，如市场分析、方案选择等。常用的求解算法基本分为两类，一类是确定性算法，如分支限界法；一类是启发式算法，如蚁群算法、智能搜索算法等。但是随着社会的发展，图也越来越大，一些常用的算法局限性也暴露出来，于是，人们的开始寻求突破。随着DNA分子的研究的进展，DNA的高并行性、操作性强，储存信息广的优势出现在人们的视野中，开始着手于利用DNA计算解决这类NP问题。

Adleman[23]对一个7顶点6条边的图进行DNA编码，成功的求出了该图的Hamilton路径。Ouyang[24]等就已经借助DNA计算求解图的最大团问题。Yang[25]等构造了圆形DNA分子模型求解最大团问题。文献[26-27]分别利用DNA三维自组装算法和粘贴模型成功的求解了图的最大团问题。李艳梅利用DEM求解图的最大团[28]。陈芳等利用三链DNA求解最大团问题[29]。

本文主要是利用DNA折纸系统求解最大团问题，该折纸系统由DNA步行器、双DNA机器和DNA折纸卡槽三部分组成[30]。我们首先对图中的各个顶点进行指派，排列出所有可能的情况，生成数据池，然后利用DNA折纸系统进行筛选，移除不符合团定义的DNA步行器，最后利用于补图进行检测，根据在透射电镜下DNA步行器手上发夹结构的个数，来判断和读取最大团。

2 DNA折纸系统

该系统由一个三角形形状的DNA步行器，双态的DNA机器和DNA折纸卡槽三部分组成，如图1。其中，三角形的DNA步行器是由7条3’端为粘性末端的单链DNA折叠而成的折纸结构，这些粘性末端充当DNA步行器的“手”和“足”。“手”分别用 H1～H3 表示，“足”分别用 F1～F4 表示，F4被固定在在DNA折纸基底上，并且每条手上绑有2种不同大小的发夹结构，共6个发夹结构，分别用a～f来表示。该DNA步行器借助链置换在折纸基底上旋转移动。

图1DNA折纸系统基本组成

图1(b)所示的双态DNA机器，能够捕获特定信息，定向识别的机器。两种状态分别为PX和JX2。当处于PX状态时，表明接收或者捕获预定的信息。当处于JX2状态时，表明不接收或者拒绝信息。图1(c)展示的是DNA折纸卡槽，该折纸卡槽是由一条M13链和202条短链折叠而成，下方是折纸基底，基底上延伸出9条单链，组成3个三角形的站点，充当DNA步行器装配的轨道，站点上方的3个白色的方框为3个插槽，分别与双态的DNA机器通过互补的单链连接。

图2中左侧中间的三角形为带有发夹结构的DNA步行器。该DNA步行器借助链置换在折纸基底的轨道上行走，每走一步，顺时针旋转120°。当整个组装完成后，可根据透射电镜观察DNA步行器上发夹结构的个数来判断最后的接收的信息是不是满足预定的结果。

图2 组装完成后，处于PX状态的DNA折纸系统

下面将分别阐述DNA步行器是如何行走的和如何进行链置换反应解开发夹。

处于PX状态的DNA机器如图3，DNA步行器手上发夹结构解开的过程。在解开发夹结构的的过程中，主要是DNA机器和DNA步行器的手H1通过链置换反应进行的。图3(a)是的DNA步行器处于的PX状态的DNA机器相接近，图3(b)是的DNA步行器的一只手上的发夹与处于PX状态的DNA机器进行链置换，图3(c)是处于PX状态的DNA机器与解开DNA步行器手上一个发夹结构逐渐远离的过程。

DNA步行器从一个站点到下一个站点行走的过程，如图4。数字1～7分别组成DNA步行器的 7 条单链，1～3 是它的“手”，4～7 为其“足”。O—*是从折纸基底上延伸出来的9条辅助单链，充当3个三角形的站点，起到辅助步行器行走的作用。A—*是步行器足上锚链，能够与O—*和DNA步行器的足互补。FA—*是能够与A—*完全互补的短链，其可以与DNA步行器的足发生链置换，解绑DNA步行器与折纸基底的链接，让DNA步行器在预定的轨道上进行行走。图4左侧是行走机器人处于第一个站点，此时的DNA步行器被固定，“足”4和5分别被单链A-1和A-2捆绑在单链O-1和O-3上，“足”7也被单链A-4捆绑在单链 O-2 上，“足”6,没有被捆绑。“手”3 慢慢接近处于PX状态的DNA机器，以便进行链置换，解开发夹。开始添加短链FA-1和FA-4，使单链A-1和A-4被解绑出来，“足”5和7被解绑，“足”4依旧被捆绑着，同再添加A-3将“足”6和A-4固定，“足”7没有被捆绑，这时的DNA步行器旋转了120°，向前前进了一步，处于第一站点与第二站点中间位置。中间是DNA步行器在第一站点与第二站点中间位置的状态，此时添加单链FA-2与单链A-2发生链置换，此时单链4与O-3解绑，“足”6这时被捆绑，接着添加单链A-5将单链5与O-6绑定，加入单链A-6将“足”7捆绑在O-5上“手”2慢慢接近处于PX状态的DNA机器，去解开发夹右侧，这时的DNA步行器再次顺时针旋转了120°，再次向前行走了一步，位于第二站点。从第二站点到第三站点DNA步行器在预定轨道上行走过程相似。当DNA步行器到达第三站点后，DNA步行器的“足”可以通过添加绑定链的互补链进行解绑，这时DNA步行器被置换出来。当DNA步行器置换出来后，再次将其和组装折纸基底进行检测，再次行走的过程和前面类似，当DNA步行器再次被置换后，进行解的读取。

图3 DNA步行器上进行链置换解开的三种发夹结构

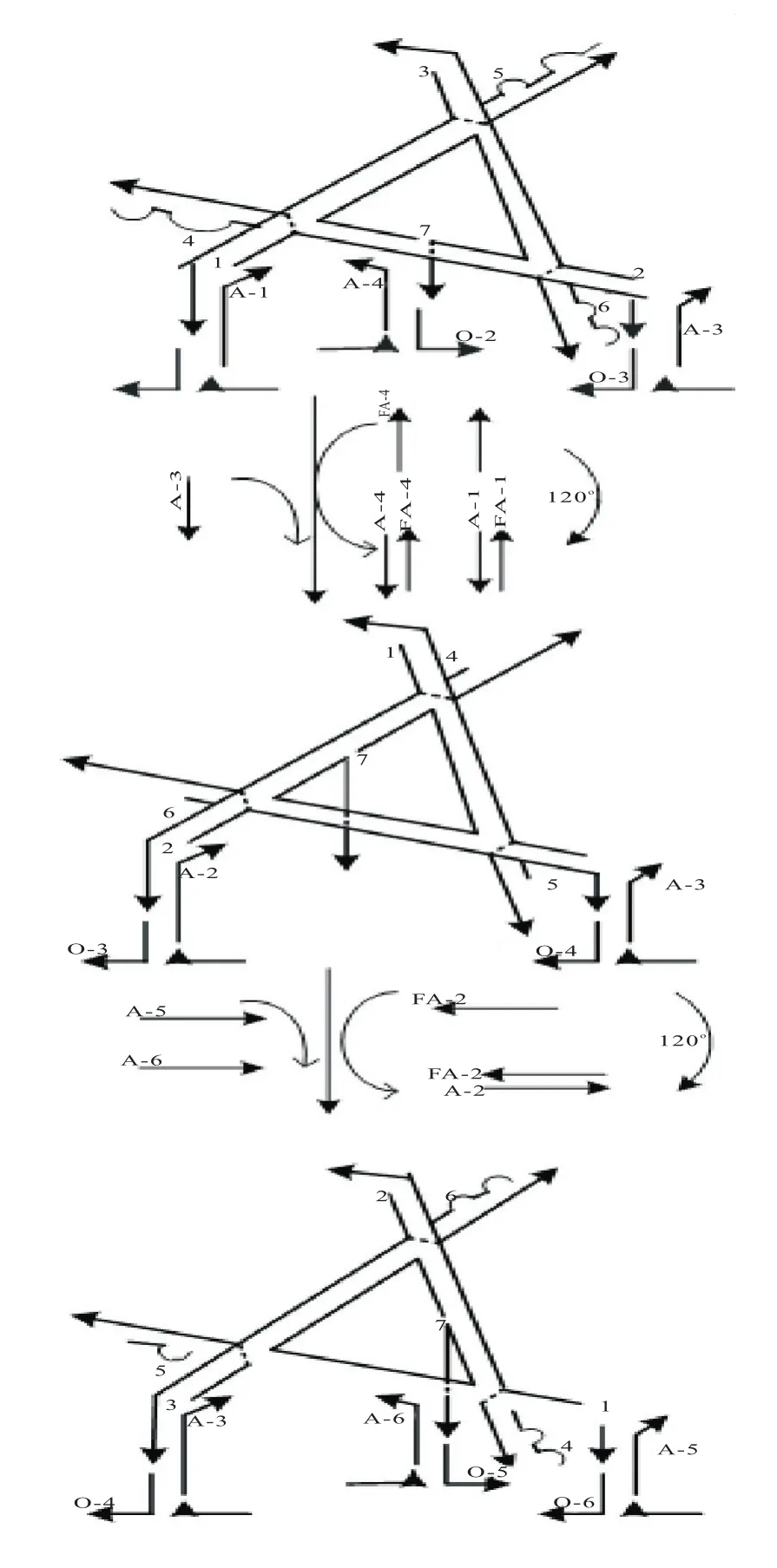
图4DNA步行器行走示意图

3 最大团问题

3.1 最大团问题

给定无向图G=(V,E)，其中V是非空集合，是图G顶点集；E是图G的边集，设U是G的一个顶点子集，对任意两个顶点u，v∈U，都和E中的边相邻，则称U是图G团。若对G任意的其它团U'都有则U是G的最大团。

3.2 最大团基本算法

对于n个顶点简单图来说，可以利用0和1的形式来指派，即当图的某一顶点在团中，用1指派，当图的某一顶点不在团中，用0指派，即如果该顶点在团中取值为1，不在团中取值为0。因此，可以用0和1的构成的n位字符串来表示全部组合的情况，则称这些n位字符串构成的集合为数据池。为了符合最大团的定义，因而对数据池进行筛选，保留真正的解。

Step 1:对每个顶点进行指派，折叠出代表不同顶点的DNA步行器（利用步行器手上绑有发夹结构进行顶点的区分），即生成的数据池。

Step 2:为了符合最大团的定义，需要对数据池各个顶点进行筛选。同时，我们借助图的补图进行求解，对一个图来说，团在其中，则团中各个顶点都是邻接的，那么在其补图中，该团对应的就是空图。意思就是，在补图中相邻接的两个顶点，在图中就是不邻接的，那么这两个相邻接的顶点就不可能在同一个团中。因此，对指派的字符串，图中相邻的两个顶点不可能同时为0，而在其补图中，相邻接的两顶点不会出现同时为1。因此，借助组装完成后的DNA步行器进行观测，折叠出在补图中相邻接的两个顶点的发夹结构的DNA步行器，然后加入到组装完成的折纸基底，通过逐步的链置换，进行顺时针120°旋转，解开DNA步行器手上的发夹，能够解开发夹结构，就是其补图中相邻接的两顶点，则该顶点不在团中。筛选出能解开发夹结构的DNA步行器，移除不能解开发夹结构的DNA步行器，余下的就是符合团定义的。

Step 3:借助透射电镜进行观测组装完成后置换出的DNA步行器，根据手上发夹结构的个数，找出最大团以及判断最大团中顶点的个数。

4 实例分析

以图5为例给出利用DNA折纸系统求解最大团问题。

Step1：对图中各个顶点进行指派，生成数据池。由于某一顶点可能在团中，也可能不在团中，故每个顶点有两种不同的指派。图5有6个顶点，则有12种不同的指派，即10和11,20和21,30和31,40和 41，50和 51,60和 61。下面对顶点进行区分，若Vi在团中，由定义可知，Vi=1，则不在其补图中。若Vi不在团中，由定义可知Vi=0，则在其补图中。如图 中 顶 点V1、V4、V5构 成一个团 ，用（100110）来表示。由此团中所有的可能性组合为26种，称该集合为数据池。故寻找最大团，就是找其补图中所含顶点最少的DNA步行器上的发夹结构，即发夹结构个数最少的DNA步行器。下面设计DNA步行器每只“手”上的发夹结构。

接着利用DNA折纸折叠出绑有发夹结构的DNA步行器、双态的DNA机器、DNA折纸卡槽。将绑有发夹结构的DNA步行器分为12组，前6组的代表顶点在团中，分别记为PV1,PV2,…,PV6，分别对应于V1=1，V2=1，…，V6=1。后 6 组的代表顶点不在团中，分别记为分别对应于V1=0，V2=0，…，V6=0。对顶点进行区分，包含6顶点的团对应于（111111），空图对应于（000000）。

Step 2：利用补图进行检查补图中相邻接的点，通过DNA折纸直接获得最大团，图5（b）中，顶点V1和V3、V6邻接，顶点V2和V4、V6邻接。由此可知，数据池中V1和V3同时存在（指派分别为11和31），V1和V6同时存在（指派分别为11和61），V2和V4同时存在（指派分别为21和41），V2和V6同时存在（指派分别为21和61）。

图5 6顶点的简单图及其补图

这里对V1和V3邻接的情况进行解释，将数据池分为两组：I组：只含有 11，II组只含有 31，分别加入到折纸基底上进行自组装。将折纸基底组装完成后，将DNA步行器组装进去。为了使DNA步行器能够逐步向前旋转移动，则逐步的加入DNA短链：

最后再加入FA-7,FA-8,FA-9，目的是将DNA步行器置换出来，整个组装过程DNA步行器两次被置换出来，因而需要再次将DNA步行器同折纸基底进行组装，当第二次置换完成后，满足条件，进行解的读取。经过一系列的旋转、自组装，I组中代表11的发夹结构解开，II组中代表31的发夹结构解开。然后在将I组和II组混合，这样数据池中就再不包含V1和V3同时存在的情况。借助透射电镜观测，从该系统中直接观测的折纸结构结果如下：

对于补图中的V1和V6、V2和V4、V2和V6，进行和顶点V1和V3一样的折纸自组装。这样最后的数据池中就全部是符合团定义的顶点。

Step 3：找出最大团以及最大团中顶点的个数，可以借助透射电镜观察，数据池中符合团定义的绑有发夹结构DNA步行器。因为是借助补图完成的，所以找最大团就是找补图中符合团定义的绑有发夹结构个数最少DNA步行器，从该系统中观察到最大团的折纸结构为：

可知，图5中图G的最大团为（V1V2V3V4V6），对应于（111101）。

5 小结

本文利用DNA折纸术的原理，设计了DNA折纸系统，并将其应用于求解图的最大团问题。该系统主要包括DNA步行器、双态DNA机器和DNA折纸卡槽。首先对图中的顶点进行指派，组合出所有可能的情况，生成数据池。然后利用DNA折纸系统进行筛选，筛除不符合团定义的DNA步行器，最后利用于补图进行检测，通过根据透射电镜观察DNA步行器手上发夹结构的个数，读取最大团。该系统不仅具有可预测性和可编程性等特点，而且实验操作，摆脱了试管的束缚，解决的问题的速率也大大提高。实验的结果通过电镜就可以观察的到，十分便捷。不过这种方法任有一些不足，如给定图的最大团的顶点数不能过多，同时发夹结构设计的不能太大。这个缺陷需要进一步改进。