基于遗传算法的地下燃气管道泄漏定位

张双双，李 季，袁宏永，付 明

（1.安徽理工大学电气与信息工程学院，安徽淮南232001；2.阜阳师范大学物电学院，安徽阜阳236032；3.清华大学合肥公共安全研究院，安徽合肥320601）

随着我国国民经济的日益提高以及“西气东输”工程的开展，人们对燃气的需求也日益的迫切。管道燃气不断增加的同时燃气泄漏事件时有发生。一旦发生燃气泄漏将会给人们的生命财产安全及社会经济环境带来极大的损失[1]。因此，对燃气泄漏的及时监测及精准定位至关重要。

燃气管道泄漏检测定位法主要有空气采样法、泄漏检测电缆法、漏磁试验、光纤试验、压力梯度法、负压波法、流量平衡法、统计决策法等[2-7]。它们都存在对管道线性要求高、定位精度低的缺点。针对现有燃气管道泄漏检测定位难的问题，本文提出一种基于遗传算法的定位算法对地下燃气管道泄漏进行检测定位。该算法通过对次声波强度数据分析计算，来得到泄漏点的精确位置。

1 移动感知节点数据采集方法

本文提出的算法主要是对多个移动节点获取的次声波强度数据进行运算，这些节点根据次声波强度大小来确定移动方向。其移动原理如下：在检测过程中，按照先横向再纵向的检测顺序。在横向上，根据多点的检测数据，每次向次声波强度值大的节点方向移动，直至检测到最大声波强度值，不再移动；然后保持横坐标不变，同理在纵向上移动节点，确定纵坐标。

横向节点的移动分为两个步骤，第一步是等距移动确定泄漏范围，第二步是逐步缩小范围逼近泄漏点，具体数据采集过程如下：

（ⅰ）横向上保持相邻节点等距的原则移动感知节点。首先，初始化各移动节点及初始化移动节点序列号i(-3≤i≤3)，建立坐标轴且令y=0，使得相邻节点之间距离均为e，采集各节点的横向坐标xi、次声波强度值Ii。然后，比较各节点声波强度的大小，将次声波强度值小的节点移向声波强度值大的方向，并保持相邻节点之间距离不变，再次获取各个节点的位置信息、次声波强度数据。重复以上步骤，移动节点k次，直至出现中间节点采集的声波强度数据值明显高于其相邻两侧节点获取的数据时，停止移动节点。

（ⅱ）选取步骤（1）确定的次声波强度最大的节点两侧节点坐标，记为xa、xb(k-3≤a＜b≤k+3)。将采集到强度值最小的装置移至强度值最高的两检测装置之间，该传感器横坐标记为xk+4，此时被移动的装置与原数据值最大的检测装置之间距离缩小为原距离的一半，即，再次确定各传感器检测的次声波强度和坐标，并比较声强大小确定节点再次移动的方向。依此种方法，直至将相邻传感器调整到极小的范围之内，即相邻传感器距离值≤μ(μ为预先设定的最小相邻传感器距离)。

（ⅲ）若在以上两步骤的次声波检测过程中，出现某一位置的次声波强度值明显低于其两侧位置的数据，则认为次声波传播到此处的过程中发生了较大的反射作用。因此，要对该处次声波强度做出反射补偿后，再与其它位置检测装置检测到的数据进行比较，确定检测装置移动的方向。

2 燃气泄漏感知信息的预处理

从移动节点获取的次声波信号是多泄漏源耦合并且包含了大量噪声的信号，因此必须对获取的数据做小波去噪和解耦算法的预处理。

2.1 小波去噪

环境中的噪声信号，导致获取的次声波信号不够纯净，影响定位精度。通过小波变换算法，保留有用特征量的次声波信号，去除无用的噪声信号，消除噪声影响[8-11]。小波去噪步骤：

（ⅰ）对含噪声的信号I(x)进行离散小波变换，得到各尺度小波系数Wj,k。

确定二进小波Ψ(x)，对于任意整数k，记:

式中，a为尺度因子，b为中心参数，这里取a=2-k,b=n2-k(n∈Z)。

信号函数I(x)的二进制离散小波变换Wj,k

（ⅱ）对尺度系数Wj,k进行阈值处理，得到估计的小波系数。

传统的硬阈值处理所得的估计信号会附加振荡，得到的估计信号会出现部分信号特征丢失的现象，造成信号失真。为弥补传统阈值处理的不足，采用导数连续的阈值函数进行阈值处理。

式中，l=0时，该式为标准的软阈值函数；当l＞0时，有连续的l阶导数。

（ⅲ）利用进行小波重构，得到信号I(x)的估计信号),即为去噪后具有有用特征的信号。小波重构函数为：

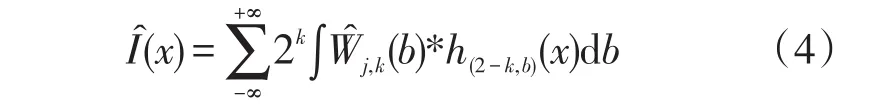
其中函数h(x)满足

式中H为阈值函数。

2.2 多泄漏源声波解耦合

燃气管道的泄漏源可能不只一处，因此经过去噪处理后得到的是多源耦合信号。为分清每个泄漏源发出的次声波信号，必须通过解耦算法解除信号之间的耦合关系[12-17]。

假设某一区域有n处泄漏，对去噪后的信号解耦合之后，每一位置可以得到n个对应的输出强度。设∑0=(A,B,C)是一个n维输入、n维输出的受控系统：

u为输入泄漏源，为输出次声波强度。

多变量系统耦合示意图如图1所示，解耦前传递函数矩阵：

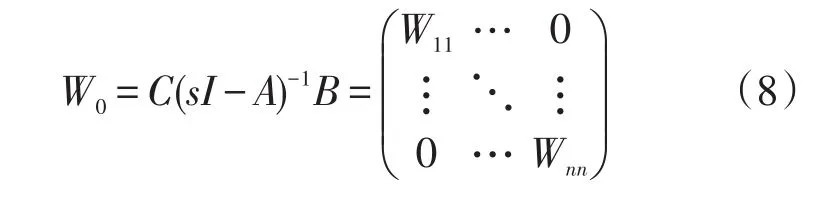
图1 多变量系统耦合示意图

本文采用的解耦方法是前馈补偿解耦，给系统设计一个前馈补偿器，达到解耦目的。设前馈补偿器的传递函数为Wd。根据设计的前馈补偿器对x-3处检测装置采集的次声波信号进行解耦，解耦后示意如图2所示。

串接前馈补偿器后系统的传递函数矩阵

图2 多变量系统解耦后示意图

所以，前馈补偿器传递函数

经过小波变换和解耦算法后，即可得到降噪解耦的次声波信号（i表示移动节点位置序列号，Iin表示序列号为i的移动节点接收的由第n个泄漏un源产生的次声波强度）来进行精确定位。

3 燃气泄漏点的精确定位

经过预处理得到的数据降噪无耦合，用预处理后的数据作定位计算，主要步骤包括反射补偿、函数拟合和遗传算法寻优函数极大值，进而确定泄漏点位置。

3.1 次声波反射补偿

由采集的数据知，次声波强度与地理坐标并不是完全的线性关系。这是因为次声波在传播过程中受到了非线性因素的影响，使得次声波强度出现了衰减。造成次声波衰减的因素主要是传播过程中遇到障碍物时发生了反射现象。在信号检测过程中，若某一位置检测到的次声波强度数据明显低于其两侧的强度，则可认为次声波在传播过程中发生了折射现象。为了达到高精确度的定位目标，需要对采集的次声波信号做反射补偿。补偿之后的次声波强度与地理位置函数关系为：

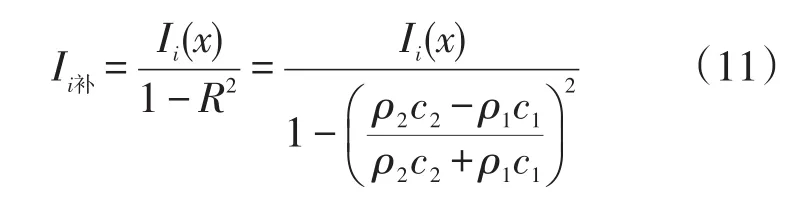
式中R为声波反射系数且ρ为介质密度，c为声波传播速度（次声波传播介质密度及传播速度均可查阅相关手册获取），Ii(x)为次声波强度的检测值，Ii补为次声波补偿后的强度值。

将补偿后的数据与其他位置的检测数据进行比较，确定检测装置移动的方向。

3.2 次声波强度与坐标的函数拟合

由数据获取、数据预处理两步，得到了降噪和无耦合的声波强度。定位前，计算机首先将横向上检测到的各个时刻各移动节点的位置坐标与预处理及补偿之后相应的由泄漏源产生的声波强度数据拟合成一个关于次声波强度与横坐标的函数x=f(1)，并导出反函数I=f-1(x)=C0e-0.017x，式中C0表示泄漏源位置处的次声波强度（不同泄漏源C0不同，但都是正定值对定位无影响），根据反函数求出次声波最大时的横坐标值。

3.3 遗传算法求次声波强度最大值位置坐标

本文采用遗传算法寻优求反函数极大值，来确定次声波强度极大值位置，从而进一步确定泄漏点位置[17-20]。次声波强度最大值坐标确定的原则遵循先横向再纵向：先在横向上通过遗传算法对函数f-1(x)在特定范围(xm,xm+1)内计算出最优极大值，确定横向声次波强度最大值横坐标；同理，确定纵向强度最大值纵坐标。遗传算法求函数f-1(x)极大值最优解的算法构造过程分为五步：

（ⅰ）确定决策变量为横向检测坐标值x和约束条件为x∈(xm,xm+1)且均小于等于100 m，建立优化模型，确定目标函数J(x)。

（ⅱ）确定编码方法。用长度为10位的二进制编码来表示决策量x。10位二进制编码可以表示从0～1 023之间的1 024个不同的数，将的定义域离散化为1 023个均等的区域，包括两个端点在内共有1 024个不同的离散点。从离散点xm到xm+1，依次分别对应于从0000000000～1111111111之间的二进制编码，每个10位二进制编码都表示一个个体的基因型。这种构建的10位编码的方法就是反函数f-1(x)优化问题的染色体编码方法，并且解空间和遗传算法的搜索空间具有一一对应的关系。

（ⅲ）确定解码方法。将10位二进制编码转换成对应的十进制整数代码，记为y。依据个体编码方法和对定义域的离散方法可知，将代码y转换为实数变量x的解码公式为：

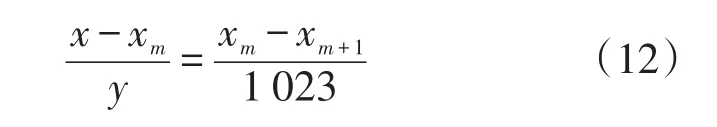
（ⅳ）确定个体评价方法。由于f-1(x)函数值为次声波强度总是非负的，并且优化目标函数是求出函数最大值，所以将个体的适应度取对应的函数值，即F(x)=f-1(x),选个体适应度的相反数作为目标函数，即目标函数值越低个体适应度就越高。

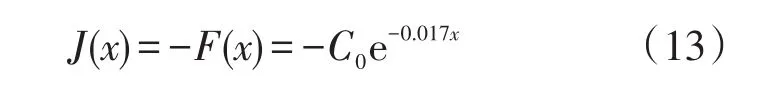
（ⅴ）设计遗传算子并确定运行数据。选择运算使用比例选择算子，交叉运算使用单点交叉算子，变异运算使用基本位变异算子，确定群体大小M、终止进化代数G、交叉概率Pc、变异概率Pm。本文Pc和Pm的取值是基于精英保留策略进行确定，精英保留策略的过程如图3。

若种群进化到第g代，计算当前代的每个个体的适应度值，挑选出适应度值最优和最差的两个。将本代最优适应度值与上一代中的最优个体比较，用替换两者中适应度值较好的第g代中适应度值最差的个体。

基于精英策略法确定Pc和Pm的公式：

式中，Pc1表示交叉概率的初始值，Pm1为变异概率的初始值，g为种群当前的代数，fc为精英策略进化过程中最优个体无变化的代数，G为种群进化总代数。

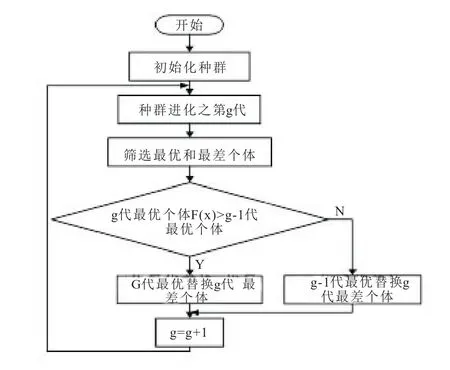
图3 精英策略进化流程图

上述五个步骤构成了用于求反函数f-1(x)极大值的二进制编码遗传算法。经过上百步迭代，通过精英策略保留了群体中适应度高的个体，淘汰了适应度低的个体，最终得到最佳样本,寻优出当x=xh时，反函数f-1(x)取得极大值。

经过遗传算法，求出当函数的极大值时的值，即确定声波强度最大值时的横坐标；同理，确定出纵向次声波强度极大值的坐标，即可确定出泄漏源的位置。

4 管道泄漏定位实验与分析

对本文提出的算法进行实验，并与传统的基于互相关时延的定位算法比较，实验验证了算法的可靠性和高准确度。

4.1 实验过程概述

以安徽理工大学能源学院安全工程实验室布建的燃气管道作为实验管道，该管道全长150 m，采用本文提出的定位算法和传统的互相关时延定位算法进行泄漏源精确定位实验并进行实验结果分析。实验分为两种类型，第一类实验是对同一泄漏点进行多次实验，分析比较两种算法定位的准确度；第二类实验是将泄漏点设置在不同点，比较算法误差。基于遗传算法的地下燃气管道泄漏定位算法的泄漏定位检测系统硬件由次声波传感器、微处理器、GPS及通讯模块组成的七个移动检测装置；软件部分主要是对采集的信号进行降噪、解耦、函数拟合、求次声波强度极大值点等处理。互相关时延定位算法系统硬件包括两个应力波传感器、微处理器和通讯模块；软件部分主要是对信号进行降噪处理和定位计算。

由于地下燃气管道并不是直线而是存在很多弯道，所以以管道首端为零点，以正西方向为x轴正方向、正南方向为y轴正方向建立坐标轴，首尾端连线与x轴正方向夹角约为2.1°。根据地下燃气管道的实际情况，第一类实验泄漏点设置在(80,7)处。第二类实验将泄漏点设置在(20,0)、(40,10)、(60,7)、(80，7)、(100,5)、(120,5)位置。基于遗传算法的定位算法的检测是在该段管道地面上并行推进检测装置，对次声波强度进行检测，遵循移动感知节点数据采集原则。与此同时，采用传统的基于互相关法的时延估计泄漏定位方法是将应力波传感器固定在燃气管道两端，采集泄漏点发出应力波到达两传感器时间差。利用两种方法对两类实验设置的泄漏点进行多次检测定位。

4.2 实验结果分析

理论上泄漏源定位应该是与实际值相吻合，但由于传感器存在灵敏度问题及数据采样保留的准确度问题，所以定位有一定的误差。定位误差的计算公式如下：

式中，x0，y0为实验中设置的泄漏设置值，x实，y实定位的泄漏源实际值，Δd为定位误差值。

第一类实验基于互相关的延时估计法将泄漏点定位在(78.3,2.9)，定位误差为4.4 m，而基于遗传算法的定位算法将泄漏点定位在(80.1,6.3)处，定位误差为0.7 m，与基于互相关的时延估计算法相比误差大大降低了；第二类实验可以看出基于遗传算法的地下燃气管道泄漏定位算法比基于互相关的时延定位算法的定位结果更稳定并且准确度更高。实验结果如表1所示。

从两类实验结果可以看出，本文提出的基于遗传算法的地下燃气管道泄漏点定位算法能够达到高精确度、高可靠性的定位，因此应用在地下燃气管道泄漏点定位中具有较高的优越性。

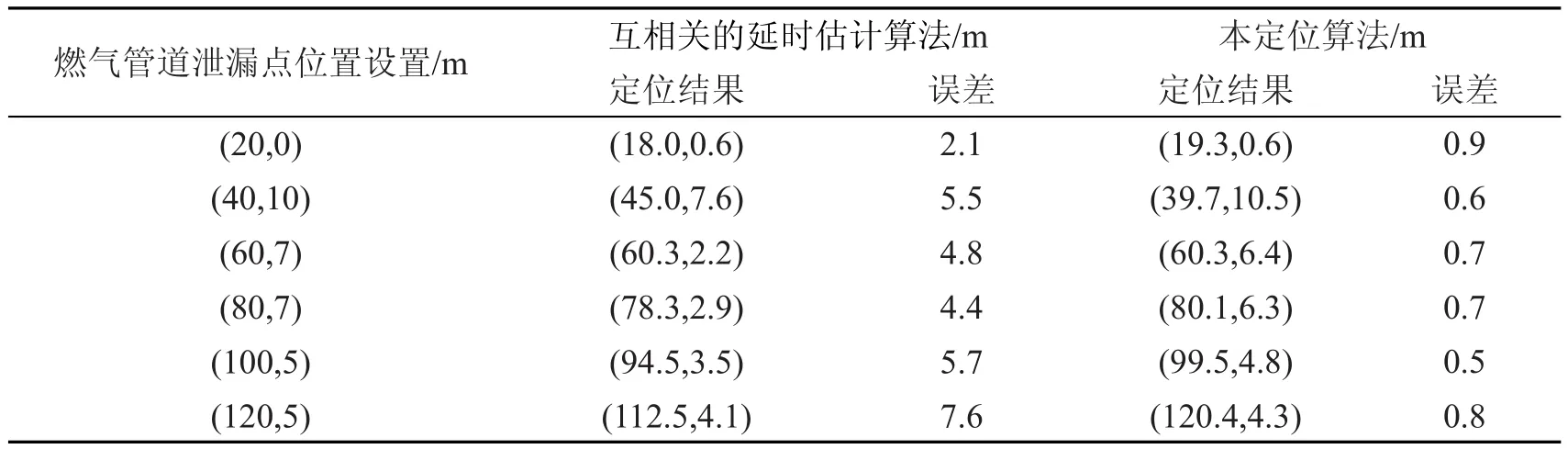
表1 第二类实验对比结果

5 小结

未来管道燃气使用会更加普遍,用量也将大幅增加，管道泄漏点定位精度问题需要得到有效的解决。文中提出的基于遗传算法的地下燃气管道泄漏定位算法，通过对泄漏点产生的次声波信号的采集、分析、补偿、运算，最终达到定位目的，弥补了传统的燃气管道定位算法精度不高、适用性不强的缺点。实验表明基于遗传算法的地下燃气管道泄漏定位算法能够达到亚米级的定位标准。下一阶段的工作主要是对该算法进行优化，降低上位机的计算量，更好的满足定位实时性的要求。