基于GWR模型的东江水质空间分异与水生态功能分区验证

和克俭,黄晓霞,*,丁 佼,刘 琦,江 源

1 云南大学资源环境与地球科学学院,昆明 650091 2 云南省水利厅,昆明 650021 3 北京师范大学地理科学学部,北京 100875

水质表征水环境质量状态,水质变化是流域地貌、水文、生物过程和人类活动等多因素综合影响的结果[1]。水生态区是淡水生态系统或生物体及其与环境相互关系相对一致的土地单元[2- 3]。已有研究指出以水生态区为基础的水污染防治体系,比单纯以工程技术为主的污染防治体系更有前景[4]。2008年我国启动国家水体污染控制与治理重大科技专项课题(水专项),系统地开展了流域水生态功能分区研究工作[5- 9]。水生态功能分区强调基于水陆生态系统的耦合关系研究,通过辨识影响水生态系统结构与功能的关键陆域或水环境因子,将这些因子的空间差异作为分区指标,揭示流域水生态系统格局与功能的空间异质性特征[10- 13]。尽管水生态功能分区以生态学理论为基础,但分区结果的科学性和合理性还有待验证,如何验证是当前亟待解决的问题。

目前,流域特征与地表水质关系的定量研究主要基于全局统计方法,比如相关分析、主成分分析、冗余分析、普通线性回归等。全局统计方法一般假定水质指标与流域影响因素之间的关系在研究区域内稳定,不随空间位置改变而变化[14]。而实际上水质与流域影响因素之间的关系可能存在局部差异,具有空间非平稳性。比如流域内不同区域,由于主导的土地利用方式不同,可能导致影响区域水质的关键因素发生变化。地理加权回归模型(Geographically weighted regression,GWR)[15]是一种局域空间分析方法,该方法将数据的地理位置嵌入回归模型中,使回归系数成为与空间位置有关的函数,其分析结果是在每个样点都会得到一组局部的参数估计。因此,GWR模型对于空间差异化关系具有强大的分析能力。作为一门新兴技术,近年来GWR模型逐渐成为土地利用对水质影响研究领域的新热点[16- 20],但目前相关研究侧重于定量描述GWR结果,少有研究将GWR结果与水生态区划结果相结合来探讨分区合理性。

东江流域是我国流域水生态功能分区研究的重点流域之一,目前已完成的一二级水生态功能分区结果主要表达了温度、降水、地形、地表覆被等大尺度环境因子影响下的区域水资源量和水质空间异质性特征[21]。本文以东江流域为例,基于大范围采样数据和GWR模型,探讨水质空间规律及其与流域因素的空间关系与水生态功能分区结果是否一致,以检验分区结果的合理性,为分区管理和水生态系统保护提供科学依据；并对比GWR模型与普通最小二乘(OLS)模型的性能,探讨GWR模型在分区结果验证中的应用价值与不足,为其他流域水生态功能分区研究提供借鉴。

1 材料与方法

1.1 研究区概况

东江(113°04′—115°50′ E,22°21′—25°12′ N)是珠江三大水系之一,发源于江西省寻邬县桠髻钵山,自东北向西南流经广东省,于东莞注入狮子洋(图1)。东江流域总面积35340 km2,干流全长562 km,地处亚热带季风气候区,多年平均气温21°C,多年平均降水量1800 mm,雨季(4—9月)降水占全年降水的80%以上[22]。

图1 东江流域采样点及水生态功能分区Fig.1 Sampling sites and aquatic ecoregions of the Dongjiang River basinR：河流型流域 River；F：东江流域编码；"I、II、III…"为一级分区编码；下标"1、2、3…"为二级分区编码

流域内主要土地利用类型为林地、农业用地(包括耕地和园地)和城镇用地,林地主要分布在北部区域,城镇用地和农业用地主要分布在中部和南部；流域地势北高南低,北部多为中、低山地,中部以低山丘陵为主,南部为沿江平原和河口三角洲；流域内坡地(坡度>7°)主要分布在北部和中部,低平地(坡度<7°)主要分布在南部；流域内土壤以赤红壤、红壤和水稻土为主(图2)。基于自然背景区域差异,东江流域被划分为3个水生态功能一级区和9个水生态功能二级分区(图1)[21]。

1.2 水质数据采样与测定

采用快照采样(Snapshot sampling)方法于2010年7月稳定流量状况(48小时内降雨小于10 mm)下共采集102个样点水样[22],样点覆盖干流及全流域主要支流(图1)。实验设计基于如下考虑：1)2010年东江流域气候特征与流域长期气候特征一致,降雨量为1787 mm,年月均温为21.3°,雨季降雨量占全年降雨量的82%[23]；2)前期研究表明营养盐和有机污染等指标的季节差异不明显[24]；3)大范围空间采样能为揭示水质空间差异提供稳健结果[25-26]。

1.3 空间统计数据库

基于水质影响因素研究相关成果[18,28- 30],本文从土地利用和自然背景两方面构建流域影响因素指标集(表1)。

土地利用数据基于2009年Landsat TM/ETM影像(分辨率 30 m)进行解译[31],基于流域特征及研究目的,将土地利用类型重分类为耕地、园地、水域、林地、草地、城镇用地及其他用地类型(图2)。土地利用指标(斑块面积百分比PLAND、斑块密度PD)用FRAGSTATS 4.0软件[32]进行计算。海拔(ELEVA)和坡度(SLOPE)指标基于分辨率30 m的ASTER GDEM(http://glovis.usgs.gov/)数据进行计算。

土壤类型数据使用东江流域1∶100万的土壤类型图(中国科学院南京土壤研究所)。根据美国农业部水土保持局(Soil Conservation Server,SCS)开发的流域水文模型土壤水文组(hydrologic soil group,HSG)的划分标准[33],参考东江流域土壤的水文物理特征[34],按照产流能力从低到高将土壤类型分为4组(表 2),水域不计入土壤水文组类别(NA)(图2)。

表1 流域环境因素指标集及基本统计特征

PLAND：斑块面积百分比 Percentage of land use；PD：斑块密度 Patch density；ELEVA：海拔 Elevation；SLOPE：坡度 Slope；HSG：土壤水文组 Hydrologic soil group；SOLAR：太阳辐射量 Solar radiation；RAIN：降雨量 Precipitation

图2 东江流域土地利用、海拔、坡度、土壤水文组、2010年流域雨季前期太阳辐射量、2010年流域雨季前期降雨量空间分布图Fig.2 The spatial distribution of land use, elevation, slope, hydrological soil group, solar radiation and rainfall during the early stage of rainy season in 2010 in the Dongjiang River basinHSGA：土壤水文组A面积百分比 Hydrologic soil group A；HSGB：土壤水文组B面积百分比 Hydrologic soil group B；HSGC：土壤水文组C面积百分比 Hydrologic soil group C；HSGD：土壤水文组D面积百分比 Hydrologic soil group D

土壤水文组Hydrologic soil group土壤质地Soil texture稳定下渗率/(mm/h)Steady infiltration rate渗透能力Infiltration abilityA砂土、壤质砂土、砂质壤土>7.26强B壤土、粉砂壤土3.81—7.26较强C砂粘壤土1.27—3.81中等D粘壤土、粉砂壤土、砂粘土、粉砂粘土、粘土0.00—1.27弱

SCS为美国农业部水土保持局(Soil Conservation Server,SCS)开发的流域水文模型

由于夏季样点间气温差异小,因此本研究舍弃气温指标,选取太阳辐射量以表征热量空间差异(图2)。太阳辐射的观测密度通常较小,采用简单的空间插值技术不能合理地揭示太阳辐射空间分布特征[35]。因此本研究采用ArcGIS 9.3软件中Solar radiation 工具模拟雨季开始至采样前(2010年4月—6月)累积的太阳总辐射量[36](天气状况：晴朗；透射率：0.5,散射比例：0.3)。并根据相邻气象站辐射日值观测数据,选取每5天中的最大日总辐射量作为晴朗天气下太阳总辐射量,验证模型模拟的精度,验证结果表明模型模拟效果较好(图3)。2010年4月—6月降雨量数据(http://cdc.cma.gov.cn/)以气象站高程作为协方差进行cokriging空间插值(图2)。

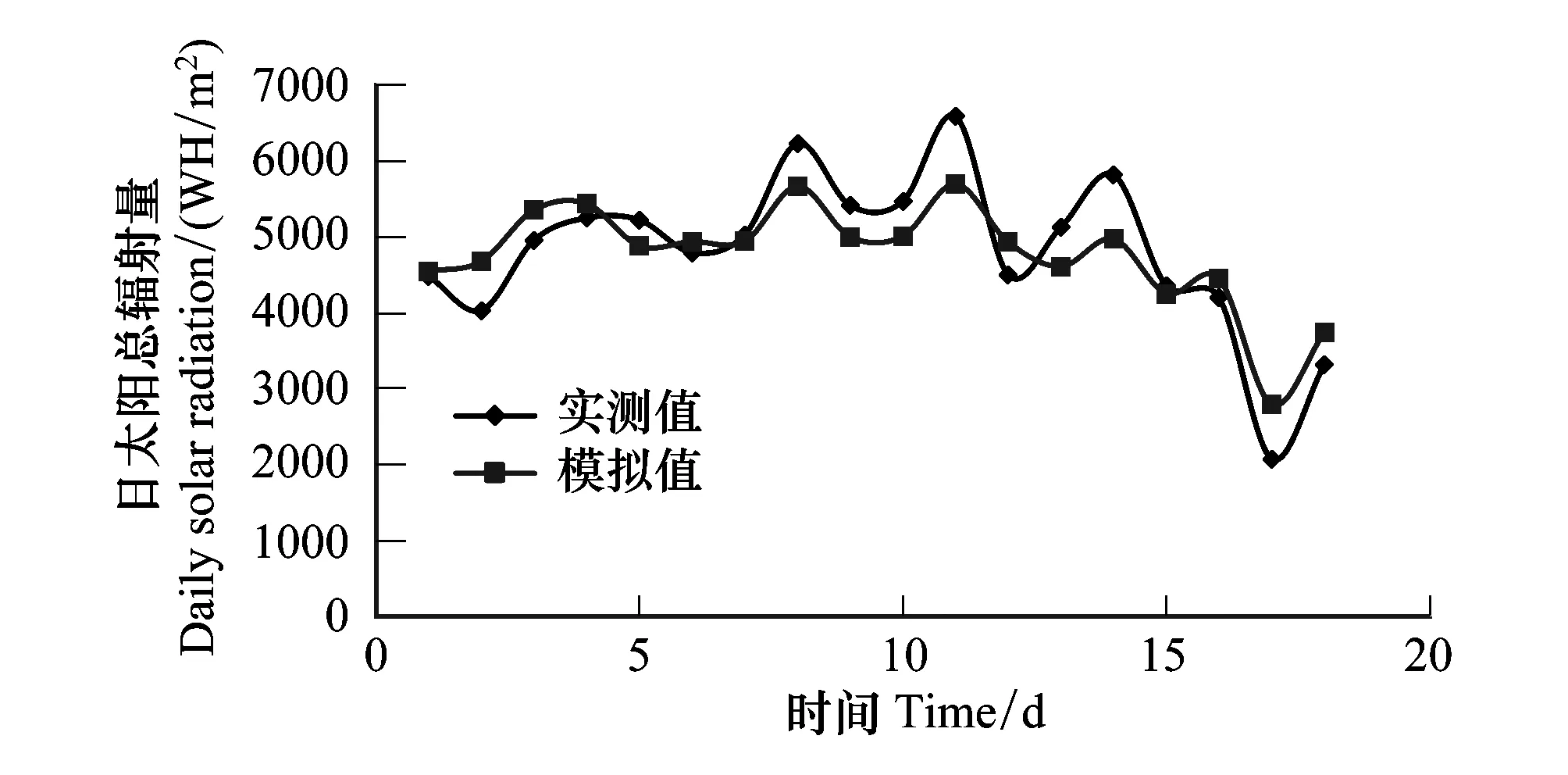
图3 日太阳总辐射量实测值与模拟值比较 Fig.3 The comparison between measured and simulated daily solar radiation

为保证样点环境数据不受邻近样点位置的影响,分别以每个样点为出水口提取其上游集水区[24],并基于每个样点上游集水区范围分别计算其土地利用和自然背景指标,共计提取612个图层进行分层统计。

1.4 统计方法

水质区域差异分析采用Kruskal-Wallis非参数方差分析,并进行Dunn多重比较(posthoctest)分析,显著性水平为P<0.05。方差分析在SPSS 21.0软件中实现；均值图在Origin 9.0软件中实现。

1.4.1普通线性回归模型OLS

采用普通最小二乘法(Ordinary Least Squares,OLS)线性回归模型,评估单个水质指标与流域影响变量之间的全局关系,计算公式[32]如下：

(1)

式中,y为因变量；xi为解释变量；p为预测变量个数；β0为截距；βi为回归系数；ε为均值为0、方差为σ2的误差项。水质指标预先进行Ln(X+1)转换,解释变量采用Z标准化。采用逐步多元回归挑选显著的解释变量进入模型。根据如下标准挑选各水质指标的最佳OLS模型：1)模型校正R2(adjustedR2)最高；2)模型参数及解释变量参数显著(P≤0.05)；3)解释变量方差膨胀因子(Variance Inflation Factor,VIF)小于3。以上操作在SPSS 21.0实现。

1.4.2地理加权回归模型GWR

地理加权回归模型(Geographically weighted regression,GWR)是对普通线性回归模型的扩展,其公式[30]如下：

(2)

式中,(uj,vj)为第j个采样点的坐标(公里网坐标)；βi(uj,vj)为第j个采样点上的第i个回归系数,即地理位置的函数；εj为误差项。根据加权最小二乘法,βi(uj,vj)可通过使

(3)

达到最小来进行估计,式中,wjk为回归点j与其他已知观测点k之间的距离衰减函数,其基本假设为距离j点越近的观测点对求解局部回归系数的重要性越大,越远的观测点重要性越小[13]。wjk为空间权重矩阵,其计算方法包括距离阈值法、距离反比法、Gauss函数法及bi-square函数法等[14- 15]。本研究选用Gauss函数计算空间权重矩阵,公式[37]如下：

(4)

式中,djk为观测点j、k之间距离；b为带宽。本研究以AICC(修正的Akaike信息准则)为衡量标准的自适应带宽形式,识别最佳自适应邻近点个数,即在数据密集地方采用较小的带宽而在数据稀疏的地方采用较大的带宽。为避免数据共线性影响,采用最佳逐步OLS模型挑选出的显著解释变量输入GWR模型。

1.4.3OLS模型与GWR模型评价

采用稳态评估Koenker (BP) 统计量[31]对OLS模型进行空间平稳性检验,若K(BP)-Prob<0.05表示模型具有显著的非稳态,即模型变量间关系存在空间差异,说明模型适合进行地理加权回归(GWR)分析。

通过比较OLS和GWR模型的adjustedR2和残差空间自相关指数(Moran′s I),分析GWR模型在预测精度和处理空间自相关过程中是否优于OLS模型。采用空间自相关工具计算模型标准化回归残差的全局 Moran′s I 指数,其计算公式[26]如下：

(5)

式中,Xi、Xj分别为要素i和j的值；n为要素个数；wij为要素i和j之间空间权重,定义为两者之间距离的倒数。如果 Moran′s I 指数值为正则指示聚集趋势,其值为负则指示离散趋势,其值接近零则指示随机模式。

GWR模型估计以及空间自相关分析均在ArcGIS 9.3软件中进行。

2 结果与分析

2.1 水生态功能分区水质差异特征

图4的Kruskal-Wallis检验结果显示：各水质指标(除NO3-N外)在水生态一级区RFⅠ与RFⅢ、RFⅡ与RFⅢ之间差异显著(P<0.05)；DO、CODMn、TN和NO3-N在RFⅠ内二级区之间差异显著(P<0.05)；TEM、EC、TN和NO3-N在RFⅡ内二级区之间差异显著(P<0.05)；EC、TP、TN、NO3-N和Chl-a在RFⅢ内二级区之间差异显著(P<0.05)。说明一二级水生态功能分区结果能较好地反映流域水质空间差异。此外,TN在一级区之间,以及一级区内二级区之间,均存在显著差异,这表明TN是理想的分区验证指标。

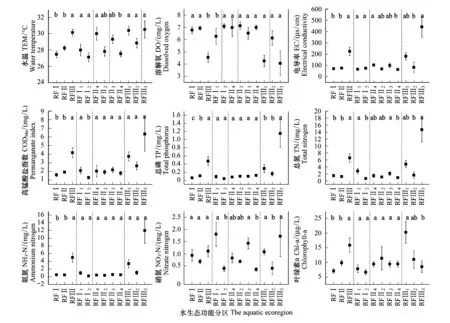
图4 一二级水生态区水质指标差异(均值±标准误)Fig.4 The differences of water quality parameters among ecoregions

2.2 基于GWR模型评估水质与影响因素关系

通过逐步多元回归筛选最优OLS模型(表 3),结果显示除了TEM和Chl-a模型解释率较低外(adjusted

LnTEM：水温 Water temperature；LnDO：溶解氧 Dissolved oxygen；LnEC：电导率 Electrical conductivity；LnCODMn：高锰酸盐指数 Permanganate index；LnTP：总磷 Total phosphorus；LnTN：总氮 Total nitrogen；LnNH3-N：氨氮 Ammonia nitrogen；LnNO3-N：硝氮 Nitrate nitrogen；LnChl-a：叶绿素a Chlorophyll a

R2<0.4),其他指标模型解释率均较高(adjustedR2>0.4),说明流域影响因素能解释大部分水质差异。GWR模型局部解释率(LocalR2)空间差异说明流域环境因素对水质的影响存在明显的空间差异,且这种空间差异与水生态功能分区结果具有高度一致性(图5和图6)。各水质指标的Local R2在三个水生态一级区(RFⅠ、RFⅡ和RFⅢ)之间差异显著(P<0.05)；除EC在RFⅠ1和RFⅠ2之间差异不显著外,各指标Local R2在一级区内二级区间也存在显著差异(P<0.05)。这说明基于流域特征的水生态功能分区结果与流域环境因素对水质影响关系的空间差异状况一致。采用GWR模型评估流域特征与水质关系的空间差异,能简单有效地验证水生态功能分区的合理性。

2.3 OLS和GWR模型性能评价

Koenker(BP)稳态检验结果(表 4)表明EC、TP、NH3-N、NO3-N、Chl-a的OLS回归模型存在空间非稳态(P<0.05),说明这些水质指标更适合运行GWR模型。通过比较模型adjustedR2和Moran′s I值,对于营养盐和有机污染指标而言,GWR模型比OLS模型具有更高的解释率,残差空间自相关性更低。表明GWR模型能改善OLS模型残差空间依赖性问题,具有更好的拟合效果。

值得注意的是,DO不仅OLS模型具有空间平稳性(P>0.05),其OLS的adjustedR2高于GWR模型,且OLS残差自相关程度弱于GWR模型,因此更适合进行OLS模型分析。此外,尽管TP模型存在显著的空间非平稳性(P<0.05),但其OLS模型和GWR模型回归残差均呈聚集状态,说明该模型缺失了某个关键解释变量,有可能是未考虑人为点源排放的影响。因此,DO和TP可能不适合作为分区验证指标。

图5 地理加权回归(GWR)模型的local R2空间分布图Fig.5 The spatial distribution of local R2 from Geographically Weighted Regression models

图6 一二级水生态区GWR模型local R2差异(均值±标准误)图Fig.6 The differences of local R2 from GWR models among ecoregions

水质参数Water quality parameters稳态评估K(BP)-Prob校正R2 Adjusted R2残差空间自相关指数 Moran′s IOLSGWROLSGWR水温 LnTEM0.1790.3670.3720.140.12溶解氧 LnDO0.0760.5060.498-0.21-0.22电导率 LnEC0.040∗0.6090.6890.310.00高锰酸盐指数 LnCODMn0.0900.5160.5210.140.12总磷 LnTP<0.001∗∗0.5890.6011.431.43总氮 LnTN0.1570.6530.6650.070.05氨氮 LnNH3-N<0.001∗∗0.6490.6530.200.18硝氮 LnNO3-N0.019∗0.4030.4500.130.00叶绿素a LnChl-a0.004∗∗0.2200.2170.460.44

P<0.05； **P<0.01

随着区划理论和技术的发展,未来的生态区划将更多的从自然、社会经济等不同的影响因素出发进行指标选取,并且指标选取的依据将更加量化。GWR模型作为一种空间明确的分析方法,不仅估计结果有明确的解析表示,而且得到的参数估计还能进行统计检验,在空间数据分析和变量关系的空间制图方面具有明显的优势,能提供传统全局统计方法无法给出的信息。因此GWR方法能够更好的用于识别区划目标要素与自然、社会经济因子之间耦合关系的空间非平稳性,为分区指标的选取、分区结果的验证、不同区划方案的直接比较等方面提供新的思路和方法。

然而GWR模型尚存在一些不足之处,比如GWR模型虽然在一定程度上考虑了数据的空间自相关,但它并没有明确地解决空间自相关问题；GWR模型基于欧式距离测度距离衰减效应,而对于河流系统而言,还应考虑沿径流网络的距离衰减效应,因此基于欧式距离的测度方式不能反映水质采样点间真实的空间接近程度。如何降低数据空间自相关带来的影响,以及使用更合适的距离测度方法,是未来GWR模型应用于水生态系统研究的难点问题。

3 结论

东江流域各水质指标(除NO3-N外)在水生态一级区之间差异显著；DO、CODMn、TN和NO3-N在RFⅠ内二级区之间差异显著；TEM、EC、TN和NO3-N在RFⅡ内二级区之间差异显著；EC、TP、TN、NO3-N和Chl-a在RFⅢ内二级区之间差异显著。说明东江水生态功能分区结果能够较好地反映流域水质空间差异。基于GWR模型,各水质指标的Local R2在水生态一级区之间差异显著；除EC外,各指标Local R2在一级区内二级区间也存在显著差异,说明流域环境因素对水质的影响存在明显的空间差异,且这种空间差异与水生态功能分区结果具有高度一致性,表明东江水生态功能分区结果能合理反映水陆耦合关系。此外,TN在一级区之间,以及一级区内二级区之间均存在显著差异,可以作为理想的分区验证指标。而DO由于模型变量关系表现出空间平稳性,TP由于OLS模型和GWR模型回归残差均呈聚集状态,不适合作为分区验证指标。GWR模型相比OLS模型具有更好的模型拟合效果,对空间数据分析和空间制图具有明显的优势,在分区研究中具有广泛应用前景。降低数据空间自相关影响及改善距离测度方法是未来GWR模型研究的难点问题。