适用于多逆变器孤岛检测的改进主动频率偏移法

2019-09-04王鲁杨

上海电力大学学报 2019年4期

李丽, 王鲁杨, 张浩, 孙皓

(1.上海电力学院, 上海 200090; 2.国网安徽省电力公司淮北供电公司, 安徽淮北 235000;3.国网山东省电力公司烟台供电公司, 山东烟台 264000)

随着新能源的迅速发展,分布式能源的利用比重显著增加。孤岛检测是分布式能源并网运行的重要环节。逆变器孤岛运行是指在公共电网中,由于故障或者维修而停止向负载供电时,分布式电源没有及时检测出公共电网处于停电状态,仍继续向负载供电,长时间孤岛运行状态将会对电气设备产生影响,对检修人员造成人身伤害。因此,孤岛检测是逆变器并网运行中不能缺少的环节。

目前孤岛检测方法主要有3类:被动检测法(Passive Islanding Detection Method,P-IDM)、主动检测法(Active Islanding Detection Method,A-IDM)和远程通信检测法(Rumor Communication Islanding Detection Method,RC-IDM)。P-IDM通过检测电路中某些电气量(如公共点电压、电网频率、逆变器输出电流等)的值是否超出正常运行的输出阈值范围来判断是否发生孤岛[1-2]。A-IDM是通过向电网注入扰动信号,在电网正常运行时,电路电气量被大电网钳制而不产生改变;若孤岛发生,电路电气量将受到注入信号的影响而发生偏移,通过多个周期的扰动逐渐偏离正常输出阈值范围,最终超出阈值的上限或下限,从而检测出孤岛的发生[3]。A-IDM能够在较短时间内检测出孤岛,检测盲区较小,但是对系统电能质量影响较大[4]。RC-IDM采用信息传送的方式,将检测的信号传递给逆变器进行判断是否发生孤岛,虽精确度高,对电能质量没有影响,但是需要借助通信技术,成本高,不适合大规模的使用。

随着智能算法的迅速发展,孤岛检测利用智能算法进行快速检测成为趋势。主要的智能算法有模糊控制法、神经网络控制法、支持向量机控制法、经验模态分解法等。目前,许多学者将模糊控制算法应用于工程控制,算法成熟。本文提出了一种基于模糊控制改进的主动频率偏移法,用于多逆变器并网运行的孤岛检测。

1 主动频率偏移法的工作特性

1.1 Sandia频率偏移法

Sandia频率偏移(Sandia Frequency Shift,SFS)法孤岛检测是通过并网逆变器向电网注入有微小畸变的正弦电流,在电网和逆变器断开形成孤岛后,公共耦合点(Point of Common Coupling,PCC)的电压频率受逆变器输出电流的影响,跟随其向上或者向下偏移,直至超出设定的阈值,从而检测出孤岛的发生[5]。以PCC的电压频率向上移动为例,逆变器输出电流如图1中虚线波形所示。电网断开后,PCC处电压频率不受电网频率的钳制,而受注入系统扰动波形的影响,PCC处电压较额定电压的频率大,经过正反馈后逐渐增大,直至设定的阈值,实现孤岛检测的功能。

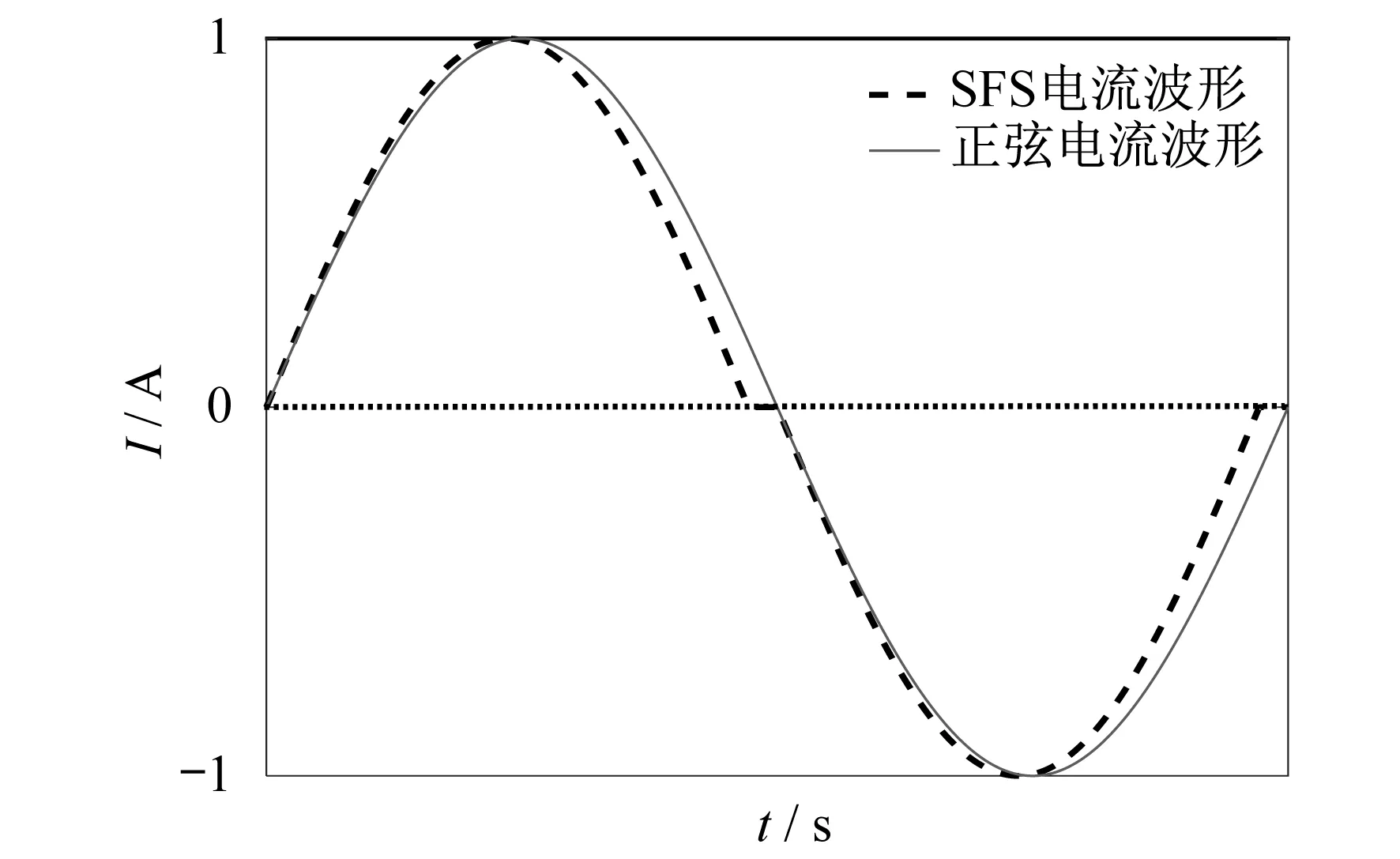
图1 主动频率偏移法的电流波形

图1中死区宽度的大小可由斩波系数表示,斩波系数越大,逆变器输出电流频率越大,其作用越明显。

传统的SFS法的斩波系数为

Cf=Cf0+k(f-fg)=Cf0+kδf

(1)

式中:Cf0——初始斩波系数;

k——正反馈系数;

f——PCC的电压频率;

fg——电网电压的额定频率;

δf——频率偏差,δf=f-fg。

因此,SFS法引入的扰动相移角为

(2)

负载的相位角为

(3)

式中:Qf——负载的品质因数;

f0——负载的谐振频率。

要使SFS法能够检测出孤岛的发生,必须满足SFS的相位偏移角变化率大于负载相角的变化率,即满足

(4)

将式(2)和式(3)代入式(4)中,可以化简得

(5)

由于负载品质因数满足Qf≤2.5,因此可求得反馈系数满足k≥0.064。通过增大k值的大小可以有效地减小孤岛检测的盲区,但是不能无限的增大,k值过大时会导致加入的扰动角过大,引入的谐波含量增大。由此可见,选择的参数要依据实际电路决定。

当发生孤岛时,f和f0之间的关系式为

(6)

由式(6)中等式约束条件可求得盲区边界曲线表达式为

(7)

式(7)中,49.5≤f≤50.5,θSFS由式(2)代入式(7)得到。由此可以画出取不同k值时的盲区曲线。

1.2 滑模频率偏移法

滑模频率偏移(Slide-mode Shift,SMS)法对逆变器输出电流施加一个偏差角[6-7],即实现相位的偏移。扰动偏差角是PCC频率和电网频率的函数。逆变器输出电流的表达式为

iSMS=ISMSsin(2πft+θSMS)

(8)

施加的扰动偏差角可表示为

(9)

式中:θm——扰动偏差角的最大偏移量;

fm——扰动偏移角最大值时对应的频率。

逆变器并网运行时,公共点电压频率被电网钳制为fg;当电网断开,即发生孤岛时,公共点频率受到逆变器输出电流频率的影响,使发生孤岛时逆变器输出电流对PCC进行扰动,从而使公共点频率超出阈值的上限或下限。要实现孤岛检测,即要满足

(10)

图2为SMS法相伴扰动角和负载相位角曲线示意。

图2 SMS法相位扰动角和负载相位角曲线示意

从图2可以看出,在f=50 Hz附近时,SMS曲线的斜率大于负载的斜率,PCC频率受逆变器输出电流的影响而发生偏移。当电网频率高于电网额定频率时,施加的相位扰动角大于零,通过正反馈的作用时PCC的电压不断增大,直至大于频率阈值的上限;当电网频率低于电网额定频率时,施加的相位扰动角小于零,通过反馈作用时PCC的电压不断减小,直至小于频率阈值的下限。

SMS法能够加快孤岛检测的速度,孤岛检测盲区较小,但是加入的相位扰动角会影响电网输出的电能质量。在负载的品质因数较高时,负载曲线的斜率大于SMS法的曲线斜率,扰动角的引入不足以让公共点频率超出阈值范围,导致孤岛检测失败。

2 SFS法和SMS法结合在多逆变器并网系统中稀释效应分析

在多逆变器并网运行系统中,各逆变器分别注入一个扰动信号,各信号通过叠加将会产生稀释效应[8-10],导致扰动信号的幅度减小,影响检测的速度和精度。

图3为两逆变器并网运行示意。

图3 两逆变器并网示意

图3中,两逆变器中一台采用SFS法,另一台采用SMS法,现对其进行稀释效应分析。

假设采用SFS法的逆变器输出电流是采用SMS法逆变器输出电流的β倍,因此两逆变器的输出电流分别为

(11)

(12)

两逆变器并网运行时PCC的输出电流为

iINV=iSFS+iSMS=

(13)

(14)

(15)

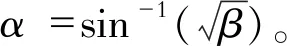
由式(15)可知,逆变器输出电流相位角满足

min(θSFS,θSMS)≤θINV≤max(θSFS,θSMS)

(16)

由式(16)可知,由于稀释效应,逆变器输出电流的相位角小于两种方法中的最大值,因此检测速度减慢。

3 基于模糊控制的多逆变器并网孤岛检测方法

通过上述分析可知,两逆变器并网运行系统由于稀释效应的存在,会导致孤岛检测速度和检测精度下降。本文提出采用模糊控制的方法[11-13],对SFS法进行参数模糊优化处理,以减小稀释效应。

3.1 SFS法系数k 的模糊控制优化

电网断电后,在未知负载特性的情况下,采用SFS法时,在k的取值范围中及时选取适合当前负载的k值是较为困难的,同时根据以往的理论分析及仿真结果来看,逆变器电压的频率偏移量和频率偏移率会受到外部扰动的干扰。模糊控制器适用于非线性、时变、滞后系统的控制,不必对被控制对象建立完整的数学模型,是一种容易控制和掌握的较为理想的非线性控制器,具有较佳的鲁棒性、适应性和容错性。此外,采用模糊控制器可选取合理的k值。

逆变器离网后形成孤岛运行状态,负载特性未知,选取特定的k值较为困难,因此选取一个二维模糊控制器。图4为二维模糊控制器的框图。

图4 二维模糊控制示意

图4中,e为逆变器电压频率fuinv与电网额定电压f0的差值。ec为e的变化率,这两者作为控制器的输入项;控制器输出项为反馈系数k;ke和kec为输入因子;ku为输出因子。选取PCC电压频率fupcc与电网电压频率fg的差值e和e的微分ec作为模糊控制的输入量,反馈系数k作为模糊控制的输出量,ke,kec,ku作为模糊控制器的量化因子。

3.2 SFS法系数k 的模糊规则

由于负载特性未知,频率差值e可能为正,也可能为负,因此选取e∈[-0.5,0.5],ec∈[-50,50],e和ec的模糊论域为[-3,3],其对应的模糊子集E=Ec={NB,NM,NS,ZE,PS,PM,PB}。反馈系数k的论域为[3,6],其对应的模糊子集U={VS,S,SS,M,BB,B,VB},E,Ec,K的隶属度函数如图5所示。量化因子ke=6,kec=0.08,ku=3。

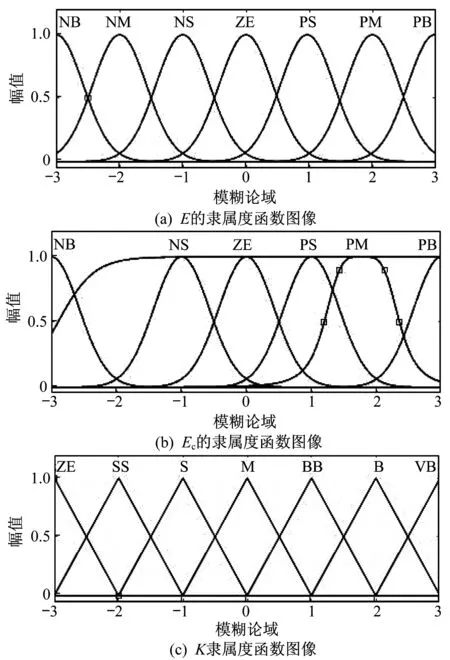
图5 输入输出变量的隶属度函数

其对应的模糊控制规则表如表1所示,模糊规则表的Surface图如图6所示。

表1 模糊控制规则

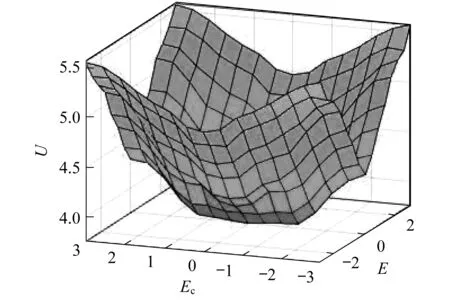
图6 模糊规则表的Surface图

根据模糊关系对应输出模糊集合,再由模糊集合得到模糊子集,将模糊子集经加权平均法转化为清晰的输出量,输出量与量化因子ku的乘积即为反馈系数k,经模糊处理后的系数k能够适应系统的特性,选择合适的k值,可以实现快速孤岛检测。

4 试验仿真

4.1 采用SFS法和SMS法的单逆变器并网孤岛检测结果

在单逆变器并网运行系统中,分别采用SFS法和SMS法进行仿真试验,以验证两种方法在单逆变器并网运行系统中的有效性。

在单逆变器运行情况下采用SFS孤岛检测法,其参数选择如表2所示。

表2 采用SFS法孤岛检测的参数选择

在单逆变器运行系统中采用SFS法进行扰动试验,检测孤岛状态。在MATLAB中的仿真结果如图7所示。图7中,在0.4 s发生孤岛,系统检测出发生孤岛,发出信号中断逆变器输出电流,在t=0.58 s时逆变器输出电流降为零,t=0.65 s时PCC的电压降为零。

图7 采用SFS法的孤岛检测仿真结果

在单逆变器运行系统中采用SMS法进行孤岛检测,其参数选择如表3所示。

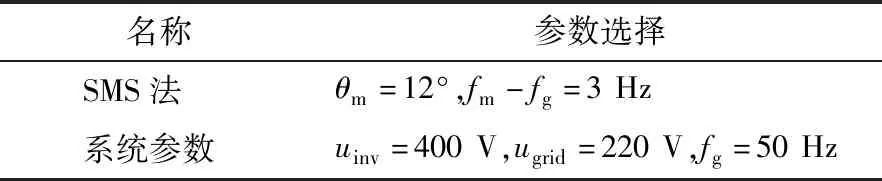
表3 采用SMS法孤岛检测的参数选择

在单逆变器运行系统中采用SMS法进行扰动试验,检测孤岛状态,在MATLAB中的仿真结果如图8所示。图8中,在0.4 s发生孤岛,系统检测到发生孤岛,发出信号中断逆变器输出电流,在t=0.53 s时逆变器输出电流降为零,在t=0.62 s时PCC的电压降为零。

图8 采用SMS法的孤岛检测仿真结果

仿真结果表明,采用SFS法和SMS法都可以有效地实现单逆变器并网运行的孤岛检测,满足国标GB/T 19939—2005要求在2 s内检测出孤岛运行状态的要求[14]。

4.2 采用SFS法和SMS法结合的多逆变器并网孤岛检测结果

在多逆变器并网运行系统中,采用传统SFS法与SMS法相结合进行扰动试验。两种方法所取参数如表4所示,仿真结果如图9所示。

表4 采用SFS法和SMS法孤岛检测的参数选择

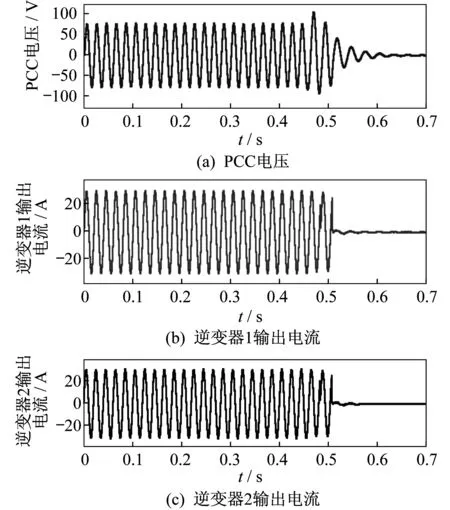
图9 采用SFS法和SMS法的孤岛检测仿真结果

图9中,在0.4 s发生孤岛,系统检测到发生孤岛,发出信号中断逆变器输出电流,在t=0.6 s时逆变器输出电流降为零,检测到孤岛发生,并发出指令使逆变器停机,在t=0.65 s时PCC的电压降为零。

表5为不同并网类型孤岛检测时间比较。

表5 不同并网类型孤岛检测时间比较

由表5可知,由于存在稀释效应,采用SFS和SMS两种方法在多逆变器并网运行孤岛检测时比在单逆变器中分别采用SFS法和SMS法的检测速度要慢。

4.3 采用模糊控制法改进的多逆变器并网孤岛检测结果

由上述分析可知,在多逆变器并网运行时,采用传统的SFS法和SMS法结合能够在2 s内检测出孤岛状态。下面采用模糊控制优化的方法进行仿真,其试验结果如图10所示。图10中,在0.4 s发生孤岛,系统检测到发生孤岛,发出信号中断逆变器输出电流,在t=0.55 s时逆变器输出电流降为零,检测到孤岛发生,并发出指令使逆变器停机,在t=0.62 s时PCC的电压降为零,满足国标GB/T 19939—2005光伏系统在2 s内检测出孤岛的要求。