椭圆中一个定值问题的拓展与思考

北京市陈经纶中学 (100020)

孟 永 张留杰

众所周知，解题训练是提升数学思维能力的一个主要途径.“如何解题”、“解后如何反思”一直是大家关注的热门话题．面对繁多的高考模拟试题，该如何应对？如何通过解一道题达到解一类题的效果？下面结合一道试题，谈谈如何把特殊问题推广到一般，探究一类问题的普遍联系，揭示试题的形成过程．

(Ⅰ)若点P在椭圆C的内部，求直线AM斜率的取值范围；

(Ⅱ)设椭圆C的右焦点为F，点Q在y轴上，且AQ∥BM，求证：∠PFQ为定值．

一、试题的解答与推广

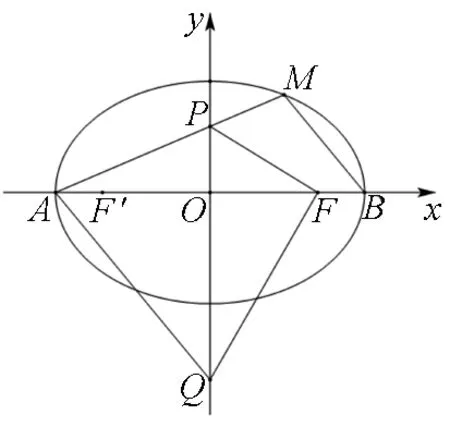
图1

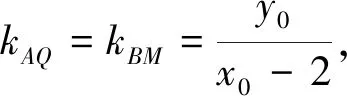
反思：回顾解题过程，不难发现在此椭圆中结论∠PFQ=90°相对于点M而言，是否具有一般性？能否推广到任意椭圆呢？带着疑问和好奇，我们进行了探究，得出了如下的结论.

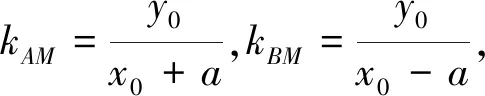
由于上述试题的b=c，自然就有PF⊥QF，所以，上述试题的结论为结论1的特例．

类似地，我们也可以将上述问题推广到双曲线中，得出

当然，若焦点在y轴上的椭圆和双曲线满足上述条件，则相应的结论也成立．

二、试题的联想与发散

高三复习过程中，遇到圆锥曲线的问题可谓无数，从一种曲线的一个特殊问题切入，将其一般化，并试图类比到其它圆锥曲线，是学习和研究圆锥曲线有效的方法之一．如果我们善于反思问题本质，联想“形异质同”的问题进行归类，总结提炼通性通法，不仅能提高学生的高阶思维能力，更能取得举一反三、融会贯通的功效，也能破解命题者改编试题的“套路”．

再回首，如果延长BM交y轴于一点，不难发现该点与点Q关于x轴对称，并且也有类似结论1的性质，于是就和下面常见的命题联系在一起．

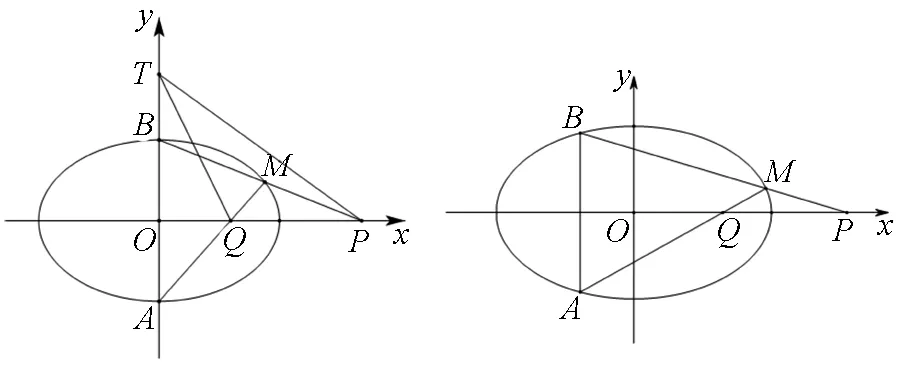
图2 图3

以上两个命题不难证明，并且还可以类比到双曲线中．

正如波利亚曾经形象地指出：“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个．”因此，在数学解题研究中，我们要善于在问题的周边寻找，梳理同类试题，探究问题的根源，使得解题走向深入．