环境规制强度与经济增长
——基于生产性资本和健康人力资本视角
2019-09-04纪建悦任文菡
纪建悦,张 懿,任文菡
(1.中国海洋大学经济学院,山东 青岛 266100;2.中国海洋大学海洋发展研究院,山东 青岛 266100)
1 引言
改革开放以来,我国经济经历了年均增长率近10%的持续快速增长。一般认为,我国经济水平的迅速提高在一定程度上得益于宽松的环境规制条件下以环境污染为代价取得的经济增长红利。长期宽松的环境规制一方面导致我国经济结构性问题突出,使企业在不承担环境成本的同时享受资源价格补贴,价格失实和盈利假象助长了企业产能规模的不断扩张,导致了严重的产能过剩。另一方面,也使生态文明成为我国经济可持续发展的最重要短板。中国环境状况公报(2016)显示,中国338个城市中,254个城市环境空气质量超标,意味着75%以上的城市大气环境质量达不到中国规定的二级标准;与此同时,中国有32.3%的地表水水质超过III类标准(不能做饮用水源),还有8.6%的地表水成为劣V类水源而几乎丧失使用功能。在此背景下,因此,实施较为严格的环境规制,对于改善我国生态环境、实现经济的可持续健康增长具有重要的现实意义。
严格的环境规制能够改善生态环境和居民的健康状况得到了学术界的普遍认可[1-3]。然而,对于环境规制如何影响经济增长的问题,相关研究结论仍存在较大分歧。已有文献大都围绕 “遵循成本说”和“波特假说”展开,具体来说:其一,“遵循成本说”认为严格的环境规制相当于对企业生产决策施加了新的约束,将增加企业的直接和间接生产成本,限制企业在创新方面投入,引致企业在生产、管理和销售方面的效率损失,不利于企业竞争力的提升。鉴于此,有研究认为严格的环境规制将降低地区的经济竞争实力,不利于经济发展水平的提高。代表性的研究主要包括:Shadbegian和Gray[1]、Christainsen和Haveman[4]、Gray[5]、Levinsohn和Petrin[6]。也就是说,如果“遵循成本说”成立,那么就存在环境保护和经济增长的“两难悖论”。针对我国的实证检验结果表明,环境规制成本引致的产出及效率损失在我国普遍存在,但不同地区、不同行业间存在着显著差异[7-10]。鉴于我国环境规制存在的巨大的“遵循成本”,许冬兰和董博[8]在研究中就曾指出,在中国现有生产方式条件下,实施严格的环境规制还存在较大难度。武晓利[9]也认为,政府的环境规制在长期能够有效改善生态环境,减少碳排放,但对宏观经济存在负效应。其二,Porter和Linde[11]提出了波特假说认为,严格且适合的环境规制强度在长期能够激励企业进行技术创新,产生“创新补偿效应”和“学习效应”以抵消环境规制成本,进而促进经济增长。也就是说,如果波特假说成立,那么就存在取得环境保护与经济增长“双重红利”的可能。目前,学术界普遍通过实证研究并使用简单的二分法来检验波特假说是否成立,具体来说,如果企业竞争力(或生产率)随着环境规制强度的提高而提升,就认为波特假说成立。反之,则认为波特假说不成立。但简单的二分法忽视了波特假说成立的基本条件,即合适的环境规制强度,得出的结论并不准确。此外,基于不同样本、不同估计方法得到的研究结论也并不一致[12-19]。Jaffe[20]梳理了相关研究成果,并根据环境规制激发的创新效应能否抵消规制成本,进一步将相关研究成果划分为“弱波特假说”和“强波特假说”。从侧面反映出对于环境规制激发的创新效应大小的问题,相关研究也没有形成比较一致的结论。但对波特假说的进一步细分有助于研究的深化。Albrizio等[21]检验了强波特假说成立与否后指出,对技术先进国家以及生产率较高的公司而言,其生产率短期内随着环境规制强度的增加而显著提升。但对创新力一般的国家或公司而言,这种效应并不显著。近年来,相关文献愈发强调企业异质性等因素对绿色创新的调节作用,注重微观层面的理论和实证研究,研究结论不断被拓展。代表性的研究主要有:赵爱武等[22]在模型中区分了异质企业主体和异质性消费者主体,认为企业绿色创新行为受到异质性需求的影响;马艳艳等[23]将现有区域或行业层面的研究细化到微观企业层面,考虑企业规模的调节作用,采用零膨胀模型实证研究了环境规制对企业创新的影响。
综上所述,虽然学术界针对环境规制与经济增长的问题已进行大量研究,但仍存在不完善之处:其一,已有研究大都缺乏理论上的深入分析,视角比较单一,基于健康人力资本和生产性资本视角展开的研究极少;其二,现有文献大都从实证的角度展开,选取不同样本、采用不同方法得出的结论也并不一致。鉴于此,从宏观层面构建合理的数理模型,深入分析环境规制影响经济增长的路径,进而确定合适的环境规制强度,并有针对性地进行宏观调控,恰恰是现阶段最重要问题。只有极少数文献从这一视角进行研究,王洪庆[24]主要基于环境规制影响劳动力学习能力的视角,分析了环境规制对经济增长存在的显著的门槛效应。但理论分析中没有考虑健康水平影响居民效用的问题,关于环境规制影响经济增长的路径分析还不够完整和清晰。鉴于此,本文基于代际交替模型(OLG模型),将环境规制强度、健康人力资本及生产性资本纳入分析框架,对环境规制强度影响经济增长的路径从理论上进行深入分析。在此基础上选取1997—2015年我国30个省级的面板数据,考虑模型存在的内生性问题,采用GMM进行实证研究,以期对已有相关研究进行补充和完善。
2 数理模型的构建
在理论分析中,本文基于代际交替模型(OLG),并将环境规制、健康人力资本及生产性资本纳入分析框架,以分析环境规制强度对经济增长率的影响。
2.1 环境规制下的居民部门决策:国民储蓄和家庭健康支出
OLG 模型假设,每个人只活两个时期:第一个时期为青年时期,每个人在年青时无弹性地提供一单位劳动力,并将劳动收入用于日常消费、家庭健康支出和储蓄;第二个时期为老年时期,居民在这一阶段只简单地消费其年青时的储蓄及其所获得的利息。假定存在人口的新老交替,即随着青年向老年的过度,原老年居民将会消亡,新一代的青年人也将出生。因此,在任何时间节点,社会都同时存在青年阶段和老年阶段的居民。在环境污染的条件下,假设居民以家庭为单位进行的健康消费支出计为T,政府的环境规制强度计为τ(其中,T>0且τ>0)。假定t时期的家庭健康消费支出和政府环境规制强度不仅影响当期青年人退休后的健康水平,同时也将对其子女(t+1期成长为青年人)的健康水平产生影响。
居民健康水平通常主要受三方面因素的影响:一是家庭健康消费支出水平T。 Grossman[25]将家庭健康支出归纳为对医疗卫生保健品的购买、加强锻炼以及为改善健康而进行的其他投入,并指出健康支出显著影响居民健康水平。家庭健康支出是决定居民健康水平的最重要因素之一,这一观点得到了学术界普遍认可[26-27];二是政府的环境规制强度τ。政府较高的环境规制强度降低了污染存量水平,能够改善环境质量,并对居民健康产生显著影响[29]。三是居民自身先天身体素质,这不是本文研究的重点,不妨简单假定为h0。鉴于此,本文健康生产函数为:
ht+1=h0·T·τ
Grossman[25]提出健康者的幸福指数更高,健康水平显著影响居民效用。因此,环境规制影响经济增长的路径之一就是影响居民的健康和效用水平。假定效用水平跨期可累加,据此给出每一代人的效用函数为:
Ut=lnCt+lnht+ρlnCt+1+βlnht+1
其中U代表效用水平;C代表日常消费支出的水平;h代表健康水平;下标t和t+1分别代表第t期和第t+1期;ρ和β为居民的主观贴现率,是居民给不同时期消费水平和健康水平的权数。
居民在年青时将劳动收入在家庭健康消费支出、日常消费支出和储蓄之间分配。而在老年阶段则将年青时期的储蓄全部用于当期消费。并假定居民是非利他的,代际之间互不关心,不存在遗赠动机。基于此,代表性个体的效用水平最大化的优化行为可表示为:
Max(lnCt+lnht+ρlnCt+1+βlnht+1)
其中,w为代表性消费者的劳动收入水平;s为代表性消费者的储蓄水平;c为日常消费支出水平;T为家庭的健康投资水平;r为居民将储蓄用于投资所获得的利息率。通过求解代表性居民的效用最大化问题可得:
(1)
等式(1)反映了地区储蓄水平的影响因素。右边的第一项的经济学含义为:在环境污染的条件下,为防止污染对健康的损害,代表性消费者倾向于选择将更多的劳动收入用于家庭健康消费支出,使居民储蓄水平趋于下降;右边的第二项的经济学含义为:收入水平是居民储蓄的最重要影响因素,并且家庭收入水平越高,其储蓄量也越大。同时,通过求解效用最大化问题,还能得到家庭健康支出的最优水平T为:
(2)
公式(2)反映了:代表性消费者的健康投资水平与其劳动收入水平正相关,说明收入水平较高的居民更加注重通过健康投资来保障自己退休后的健康水平。
2.2 环境规制下的生产部门决策:生产性资本投资量及健康人力资本形成量
如前文所述,环境规制强度的改变将影响健康人力资本的形成。大量研究指出[26-28],健康人力资本直接决定着生产过程中的有效劳动投入以及劳动的边际产出水平,主要原因在于:一是,健康的居民精力旺盛,具有较高的工作效率,能够承担更高强度的工作,其生产能力通常也较强;二是,健康人力资本水平的提升将引致平均预期寿命的延长,使劳动者工作年限趋于提高。此外,健康的居民在劳动过程中因伤病而旷工的概率也较低,这都有助于延长居民在年青时期的工作时间;三是,健康水平的提升还影响着居民的认知水平和学习能力。因此,环境规制强度还会通过影响居民健康和有效劳动投入的方式影响企业生产。
由此,应该将居民健康人力资本作为生产要素纳入生产函数,假设厂商的生产函数选取柯布道格拉斯函数形式,并表示为:
Yt=Kα(htLt)1-α
其中,Y表示总产出;K表示生产性资本水平;h代表健康人力资本水平;L代表劳动要素数量;α代表资本份额。为简化问题分析,假设L=1,即人口增长为常数,此时人均产出就是总产出:
其中y表示人均产出,k表示人均资本存量,h表示健康人力资本。厂商追求利润最大化,可表达为:
Maxπ=[(1-τ)yt-(1+rt)kt-wt]
(3)
其中,π表示厂商利润,τ表示总产出中用于治理环境污染的比例,反映了环境规制的强度。在竞争性市场条件下,劳动和资本分别获得其边际产出,厂商获得零利润,求解可得到居民劳动收入水平和资本的边际水平:
(4)
MPK=rt=[(1-τ)αyt/kt]-1
(5)
不难看出,在假定技术条件不变的情况下,环境规制强度的提升作为企业生产的额外成本,降低了厂商的利润水平,使劳动和资本的要素报酬趋于降低。
由于每一期资本由前一期储蓄决定,结合公式(1)和公式(4)可得均衡状态下的生产性资本投资量:
(6)
从生产性资本方面来看:公式(3)体现了环境规制的本质,即政府通过对污染等外部性影响纳税或罚款,使外部性成本内部化,进而弥补市场失灵,并对要素的配置产生影响。公式(6)则说明,政府环境规制强度的选择必然将直接引致生产性资本投资规模的缩减。这主要是由两方面因素的变化造成的:第一,储蓄水平的变化。公式(4)反映了环境规制强度对居民收入的影响。即严格的环境规制使企业必须为生产造成的环境污染付费,那么遵循成本的增加使企业利润水平降低,使得企业只能支付较低水平的劳动报酬。因此,在实施严格环境规则的地区,居民的工资收入水平将趋于下降。结合(1)式可知,居民收入水平的下降将导致该地区储蓄量的减少。而储蓄作为生产性资本积累的源泉,储蓄水平的缩减将抑制生产性资本的形成,最终使生产性资本的投资规模下降;第二,资本边际收益率的变化。公式(5)则反映了环境规制强度对资本边际收益率的影响,在严格的环境规制条件下,由于企业必须将高额的环境规制成本纳入自己的生产成本,导致企业利润及资本的边际收益的下降,这也不利于企业投资规模的扩张。
(7)
从健康人力资本方面来看:一方面,环境规制强度提升通过补齐生态短板,改善生态环境质量,有助于居民健康水平的提升,本文称之为“直接效应”。另一方面,环境规制强度提升将降低居民收入,并减少家庭健康支出水平,进而抑制居民健康水平的提升,本文称之为“间接效应”。直接效应和间接效应的大小比较决定了环境规制对健康人力资本的最终影响。通过求解∂ht+1/∂τ可得,除非企业将大多数用于处理环境污染,否则环境规制强度的提升将促进居民健康水平提升。但结合实际看,这几乎是不可能的。综合来看,本文认为环境规制强度的提升将促进健康人力资本形成。
2.3 环境规制强度对经济增长率影响的综合分析
基于上述分析可知,环境规制强度通过影响生产性资本投资和健康人力资本形成决定了经济增长率g,将公式(6)和公式(7)代入生产函数可得:
g=(yt+1-yt)/yt
上式对环境规制强度求导,即可得到环境规制强度提升对经济增长率的影响:
∂g/∂τ
3 实证研究
通过理论分析可知,环境规制强度的提升将对经济增长产生正负两方面影响。当环境规制强度较低时,环境规制强度与经济增长率正相关;当环境规制强度过高时,则与经济增长率负相关。下面本文将借助深入的实证研究,分析确定我国环境规制强度对经济增长率的影响。
3.1 实证模型设定
在理论分析的基础上,本文选取1997—2015年我国30个省级的面板数据,在计量模型中加入环境规制强度的二次项来刻画环境规制对经济增长的非线性影响。同时,在计量模型中引入健康人力资本水平、产业结构、人口年龄结构和储蓄水平作为控制变量。考虑如下面板数据模型:
其中,G表示GDP增长率,ENV表示环境规制强度,ENV2表示环境规制强度的平方项,HEA表示健康人力资本水平,IND表示产业结构,POPDE表示人口年龄结构,反映劳动力供给的情况,SAV表示储蓄水平,反映物质资本供给的情况。α表示常数项,μ为干扰项,反映其它未考虑到的因素对经济增长率的影响。
3.2 变量选择及说明
3.2.1 被解释变量
与数理模型相对应,本文被解释变量为经济增长率,通过各省地区生产总值计算得到。
3.2.2 核心解释变量
本文核心解释变量为环境规制强度。理论上,各国政府通常通过征收“庇古税”的方式进行有效环境规制,征收税率的高低成为反映环境规制强度最为常用的指标。但是,我国相关法律还不健全,排污权和“庇古税”等市场型环境规制手段并未充分发挥作用。相反,排污费制度实施较早,政策稳定,能够较好反映我国环境规制强度的变化[30]。鉴于此,本文通过排污费收入占地区生产总值的比重来反映环境规制强度的变化。
3.2.3 控制变量
本文选取以下变量作为控制变量:1、健康人力资本水平。国民健康水平的提升引致劳动者工作年限的延长和劳动生产能力的提高,对经济增长具有重要的促进作用,考虑数据可得性,本文选取存活率作为健康人力资本的测算指标。2、人口年龄结构。老龄化的进程决定了劳动和资本两种生产要素的供给数量和质量产生影响,必然影响经济增长[31],本文选取老年人口抚养比进行衡量。3、产业结构。我国目前正处于工业化中期,以城市工业为代表的现代经济部门与以农业为代表的传统经济部门并存,产业结构转变是影响我国经济增长的重要因素,文章中产业结构=第二产业增加值/地区生产总值。4、储蓄水平。储蓄作为资本积累的源泉对我国经济增长的影响不容忽视,文章中储蓄水平=100-最终消费率进行衡量。本文相关变量的定义及计算公式详见表1所示。

表1 变量定义表
3.3 估计方法及数据来源
本文重点研究环境规制强度对我国经济增长率的影响。然而,由于在经济发展较好的国家,居民对环境质量存在更高要求。此外,政府在制定环境保护政策时也会考虑对经济增长的影响,计量模型可能存在双向因果关系。即,计量模型存在一定的内生性。继续采用OLS方法进行估计可能存在偏误。基于此,本文采用滞后的内生变量变量作为工具变量,进行广义矩估计(GMM)。同时考虑到在使用工具变量回归的过程中,弱工具变量可能会使回归结果产生偏差,本文还对计量模型采用对弱工具变量不敏感的有限信息极大似然估计( LIML)进行回归,以保证本文结论的稳健性。
上述变量数据来自中国大陆1997—2015年的省级面板数据,西藏地区部分数据缺失严重,本文的分析没将其考虑在内。本文被解释变量为经济增长率,数据来源于《中国统计年鉴》。环境规制强度数据来源于《中国环境年鉴》。健康人力资本、人口年龄结构、产业结构和储蓄水平所需数据来自《中国统计年鉴》、国家统计局网站、《各省统计年鉴》和《中国人口年鉴》。
4 实证结果分析
4.1 描述性统计
表2给出了变量描述性统计,有助于了解各变量样本观测值的统计性属性。不难看出,各省份在经济增长率和环境规制强度方面均存在显著差异。在其他变量方面,人口年龄结构、产业结构和储蓄水平在1997-2015年间大都存在较大波动。这在一定程度上反映了不同省份、不同时期间的经济社会发展水平存在着显著差异。健康人力资本水平波动较小,但能够明显看出近年来我国居民健康水平不断改善。因此,省级的面板数据则较好地反映了这种时间趋势变化情况和区域的个体差异差异性。
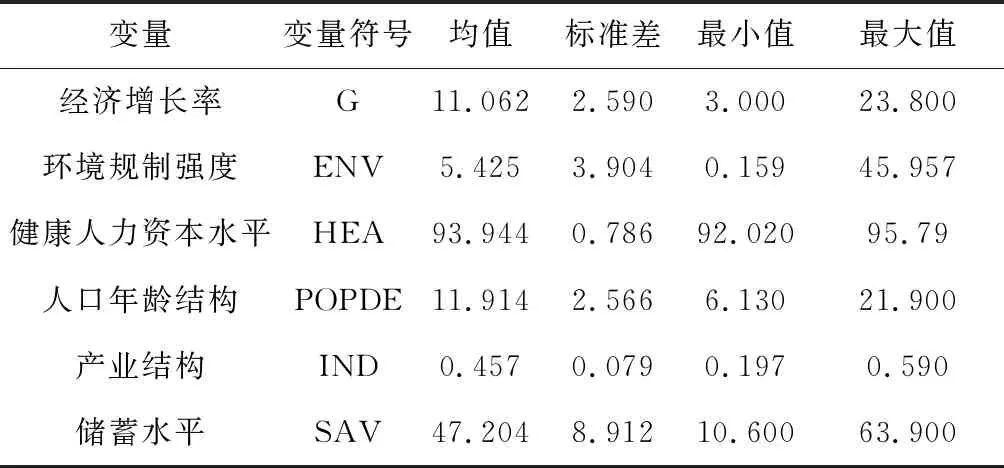
表2 变量的描述性统计
4.2 实证结果及分析
表3给出了估计结果。回归(1)-(2)分别使用了OLS和固定效应(FE))估计方法进行估计(豪斯曼检验p值为0.000,说明应该使用固定效应进行回归)。回归结果显示,经济增长和环境规制强度之间存在着显著的倒U型的非单调关系。但是正如上文所讨论的那样,由于内生性问题及遗漏变量问题的存在,不论OLS还是FE的回归结果都存在有偏和非一致的风险。但作为对照,本文仍然列出了OLS和FE的回归结果。
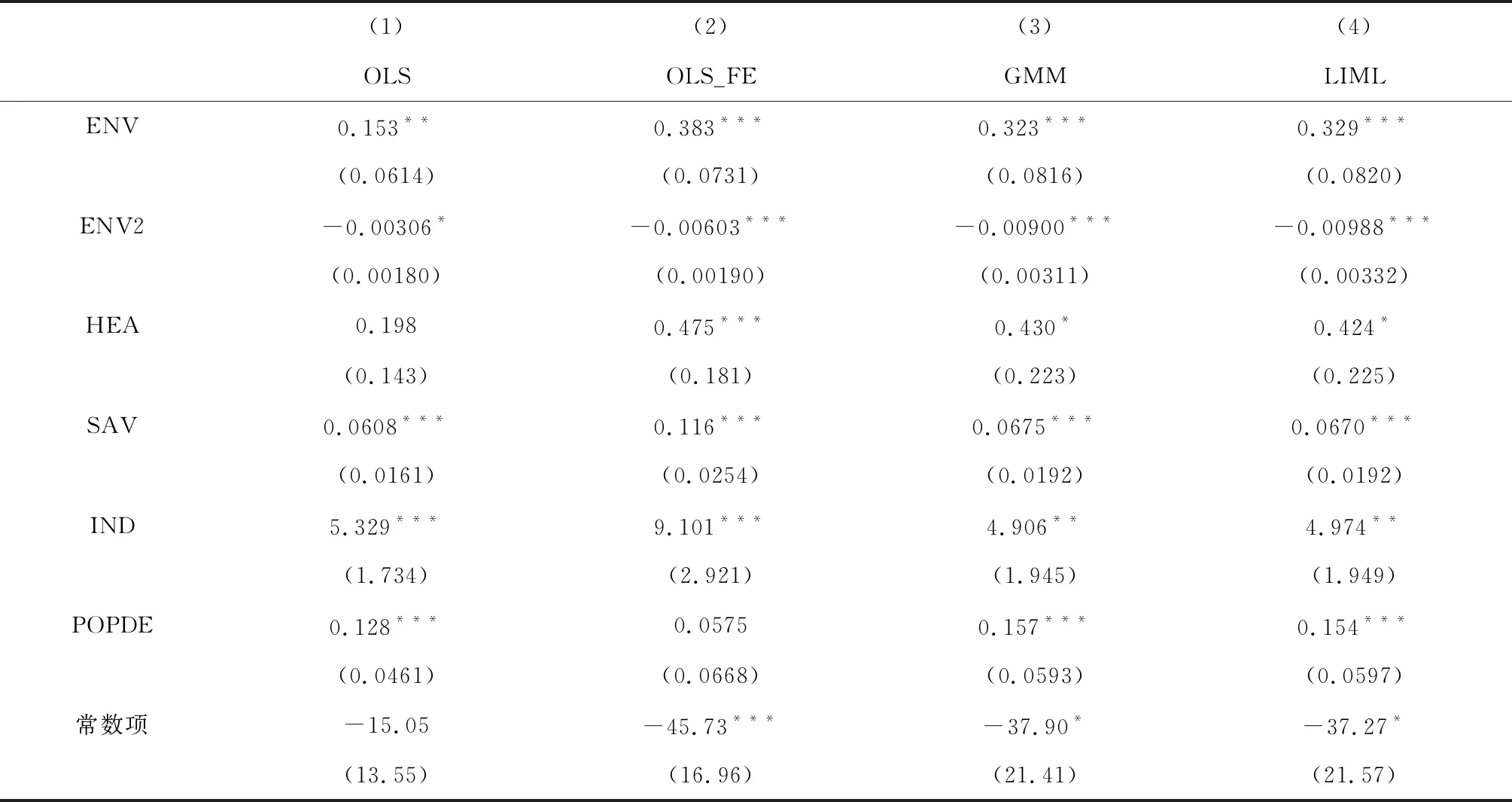
表3 估计结果
注:*p<0.1,**p<0.05,***p<0.01
本文主要研究环境规制强度对经济增长率的影响。在模型不存在内生变量的情况下,OLS将更有效。但如果环境规制强度和经济增长率之间存在相互影响,则计量模型存在内生性问题,将影响OLS回归和固定效应回归的可靠性,使OLS和固定效应回归存在不一致的风险,而工具变量法的回归结果是准确的。环境规制强度与经济增长率之间在理论上存在相互影响的可能性。对此,本文进一步通过Hausman内生性检验(结果见表4)。统计量值为15.28,p值为0.0092,可以在1%的显著性水平上拒绝“所有解释变量外生”的原假设,即认为模型存在内生性问题。但Hausman检验在异方差情形下不成立,本文还通过DWH(Durbin-Wu-Hausman)的方法进行了检验,DWH检验的P值也在1%水平上拒绝了原假设。鉴于此,计量模型存在内生性问题,应该使用广义矩估计通过工具变量进行回归。本文选取内生变量的滞后项作为工具变量进行回归,工具变量的Hansen's J统计量p值为0.4538,表明工具变量满足外生性假定。此外,Cragg-Donald Wald检验和Kleibergen-Paap LM统计量也表明本文选取的工具变量是合适的。因此,本文的工具变量与内生变量具有较强相关性,且满足外生性假定,适合作为计量模型的工具变量进行回归。在此情况下,广义矩估计的回归结果是可靠的,如表3中的回归(3)所示。回归结果显示,处理了内生性问题后,经济增长率与环境规则强度之间依然存在着显著的倒U形的非单调关系。工具变量法通常存在弱工具变量的风险,并且弱工具变量问题将严重影响回归结果,为进一步确保结论的稳健和准确性,本文还使用对弱工具变量更不敏感的有限信息最大释然法(LIML)进行回归,结果如表3回归(4)所示。不难看出,有限信息最大似然估计结果与之前广义矩估计(GMM)的回归归结果非常接近,这也进一步印证了“不存在弱工具变量”的结论。鉴于此,本文通过广义矩估计得到的回归结果是稳健而可信的。值得注意的是,由于面板数据可能存在的异方差问题,本文在回归中还添加了稳健的标准误以保证回归结果的准确性。

表4 模型内生性检验结果
总而言之,上述各种估计方法均表明:我国环境规制强度和经济增长率之间存在着稳健的倒U型的非线性关系。本文着重对广义矩估计(GMM)回归结果进行分析。回归结果显示,环境规制强度的二次项符号为负,且在1%的显著性水平下显著,拐点处的规制强度为17.94。回归结果与本文理论分析得到的结论相符。即:当环境规制强度较低时,提升环境规制强度有助于经济增长率的提高。因为在此阶段,环境规制对健康人力资本的提升效应超过了环境规制缩减生产性资本投资的效应,对经济增长起到了促进作用;但当环境规制强度过高时,环境规制缩减生产性资本投资的效应将会超过环境规制对健康人力资本的提升效应,继续提升环境规制强度将抑制经济增长。从整体上看,我国环境规制强度平均值为5.425,距离拐点还存在较大差距(如图1所示)。说明在现阶段,继续增强环境规制,能够实现环境与经济的双重红利,这就在一定程度上破解了环境和经济的“两难”悖论。
控制变量方面,健康人力资本与经济增长率在10%的显著性水平上正相关,说明居民健康水平的提升能够提高劳动者的生产能力、延长劳动者的工作年限,进而促进我国经济增长率的提高。产业结构系数在5%的水平上显著且系数为正,说明在工业化中期,工业化水平的进一步提升仍然是我国经济增长的重要动力源泉。老年抚养比回归系数为正与An和Jeon[31]的研究结论一致,印证了在老龄化的初期阶段,居民“未雨绸缪”的储蓄动机能够促进经济增长。储蓄水平在1%的水平上显著且系数为正,说明储蓄作为生产性资本积累的源泉,能够促进我国经济增长率的提高。
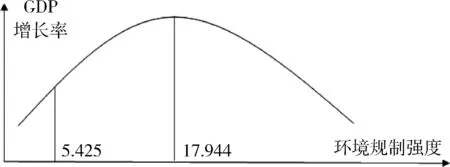
图1 环境规制强度对GDP增长率影响的示意图
5 结语
环境规制强度如何影响经济增长的问题一直是学术界关注的焦点,但极少有研究从健康人力资本和生产性资本的视角展开。针对这一问题,本文以代际交替模型(OLG)为基础,将环境规制强度、健康资本和生产性资本纳入分析框架,从宏观层面建立数理模型进行深入的理论分析。得出以下主要结论:(1)提升环境规制强度有助于健康人力资本的积累,能够提高居民的效用水平,并对经济增长产生促进作用;(2)提升环境规制强度使环境污染等外部性成本内部化,遵循成本的增加将引致企业利润水平的降低,导致要素报酬和居民储蓄量的减少,最终将缩减生产性资本的投资规模,并对经济增长产生抑制作用。(3)存在最佳环境规制强度,当环境规制强度低于最优环境规制强度时,提升环境规制强度能够促进经济增长。当环境规制强度超过最优环境规制强度后,进一步提升环境规制强度则会抑制经济增长。在此基础上,利用1997—2015年我国30个省级的面板数据,使用广义矩估计(GMM)的估计方法进行了验证。实证印证了环境规制强度和经济增长率之间存在着稳健而显著的倒U型的非线性关系。实证结果还表明,中国大多数省份的环境规制强度仍处于拐点以前,说明我国环境规制强度整体上还处于较低水平,进一步提升环境规制强度能够在不增加经济下行压力的基础上补齐生态短板,实现生态环境质量的整体改善与居民效用水平的提升。
综上所述,本文通过将环境规制强度、健康人力资本和生产性资本纳入分析框架,在比较成本与收益的基础上,对环境规制强度与经济增长率之间的关系进行理论分析,为环境规制政策的制度和环境规制强度的选择提供了重要的理论支撑。本文后续将进一步考察环境规制政策的实施效果、健康人力资本积累对企业创新的支撑以及政府环境税应用对经济增长的影响,以便使研究更加接近现实。
