大跨度铁路独塔混合梁斜拉桥的动力特性
2019-09-03康俊涛林光毅齐凯凯陈百奔张亚州
康俊涛,林光毅,齐凯凯,陈百奔,张亚州
(武汉理工大学 土木工程与建筑学院,湖北 武汉 430070)
大跨度铁路独塔混合梁斜拉桥主跨选用钢箱梁结构,可以减小自重,提升跨越能力;边跨选用混凝土梁结构作为配重,有效发挥了钢材和混凝土材质的优质特性,使其兼具混凝土梁和钢梁的优势[1]。具有代表性的工程包括深茂铁路潭江特大桥[2]、宁波北环线铁路甬江特大桥[3]、昌赣客专赣江特大桥[4]等。
近些年来,混合梁斜拉桥主跨越来越大,结构体系出现一些新的变化,需要重点考虑大跨度混合梁斜拉桥的抗震、抗风等动力问题[5]。王頠[6]研究了某钢桁公铁两用斜拉桥的索塔高跨比、边中跨之比、主梁高跨比、主塔刚度、主桁斜竖杆刚度等特征参数对其动力特性的影响规律;李永乐等[7]以某大跨度钢桁梁铁路斜拉桥为研究对象,研究梁、索、辅助墩等构件刚度对桥梁结构及行车性能的影响;刘晓光等[8]以沪通长江大桥主航道桥为研究对象,分析了边跨支点数量、边中跨比、主梁高跨比和宽跨比、塔梁高跨比等设计参数。
1 工程概况
岳口汉江特大桥采用半漂浮体系,孔跨布置为(32+50+93+260+38)m(见图1),边跨为混凝土箱梁,主跨为钢箱梁,钢-混结合段位于主跨距桥塔23 m处,箱梁标准段采用单箱三室截面,梁高3.5 m,桥面全宽13 m。全桥共设置42对斜拉索,采用扇形空间双索面布置形式。在主梁与桥塔横向连接处左右两侧各设置1个横向抗风支座,支座型号为KFBZ-2000。

图1 桥梁总体布置(单位:m)
2 桥梁有限元模型
采用MIDAS/Civil 2015建立全桥空间有限元模型,采用桁架单元模拟斜拉索,其余结构均选用梁单元模拟,结合段采用修改材料重度、换算相应刚度的方式模拟[9],全桥共划分为435个单元,519个节点。斜拉索索力采用成桥设计索力,在计算过程中假设其为柔性结构,只承受拉应力。结构自重、二期恒载等荷载均采用一致质量矩阵进行模拟。边界条件为:①桥墩与桥塔底部采用刚性连接;②斜拉索与桥塔和主梁之间采用刚性连接;③支座通过一般弹性支承模拟。
3 动力特性计算分析
采用多重Ritz向量法对该桥进行动力特性分析,该桥自振频率及振型见表1,主要振型见图2。

表1 自振频率及振型

图2 主要振型
由表1和图2可知:
1)该桥的第1阶振型为纵飘,基频为0.117 Hz,说明纵向刚度较小,充分体现了其柔性特征,与大多数半漂浮体系桥梁一致。
2)该桥振型依次为纵飘、主梁一阶竖弯、主梁一阶侧弯,振型排列合理。在前50阶振型中未出现侧弯、竖弯及扭转的耦合现象,可见该桥的主梁抗弯及抗扭刚度差异极大,不易出现耦合振动。
3)该桥振型排列紧密,具有密布的频谱,前50阶振型的振动频率为0.117~11.123 Hz,研究该桥的地震响应时应特别注意高阶振型的影响。
4)该桥第2阶振型为主梁一阶竖弯,可见其面内抗弯刚度较小;在前10阶振型中,主梁竖弯出现过5次,说明该桥的竖弯振型对动力响应起到了关键作用。
得到用户的初步认可后,可进入方案的改进阶段,此阶段的设计内容将直接最终面对用户,内容主要包括人机交互、操作逻辑、意思表达、界面美观等方面的完善。例如,在对闸门进行控制操作时,应按页面自上而下点击操作,为减少确认次数,只需在最终提交操作指令时生成操作前准备清单一次予以确认;在填写预设指令和参数时要有一定的格式判断条件,降低误操作;故障报警及事件描述应用简短精炼准确的词句;声光提示应柔和,不能太生硬;预设各种情况的描述,按照出现概率和频次进行合理排序。
4 结构动力特性的影响参数分析
材料特性、边界条件和几何构造是影响桥梁结构动力性能的主要因素。对斜拉桥来说,主要包括主梁钢混比、边中跨比、横向抗风支座、结构自重与刚度,以及辅助墩的有无等。本文选取振型为纵飘(f1)、主梁一阶竖弯(f2)、主梁一阶侧弯(f3)、主塔侧弯(f7)、主塔纵弯(f13)时的频率来分析各项参数对大跨度铁路独塔混合梁斜拉桥固有频率的影响。
4.1 主梁钢混比
主梁钢混比是混合梁斜拉桥的重要结构参数,通过改变钢-混结合段的位置来改变主梁钢混比,研究其对自振频率的影响,结果见图3。可知,当主梁钢混比由0.65变化至0.80时:①f1大幅提高,从0.091 Hz增长至0.146 Hz,增长了60%,原因是随着主梁钢混比的增加,边中跨主梁刚度发生了重分布,引起基频的变化;②f2和f3均显著提高,钢混比对主梁一阶竖弯振型更为敏感;③主塔侧弯频率减小,减小幅度在5%以内,f13基本无变化,由此可见钢混比对主塔侧弯和纵弯的影响甚微。

图3 主梁钢混比对自振频率的影响
4.2 边中跨比
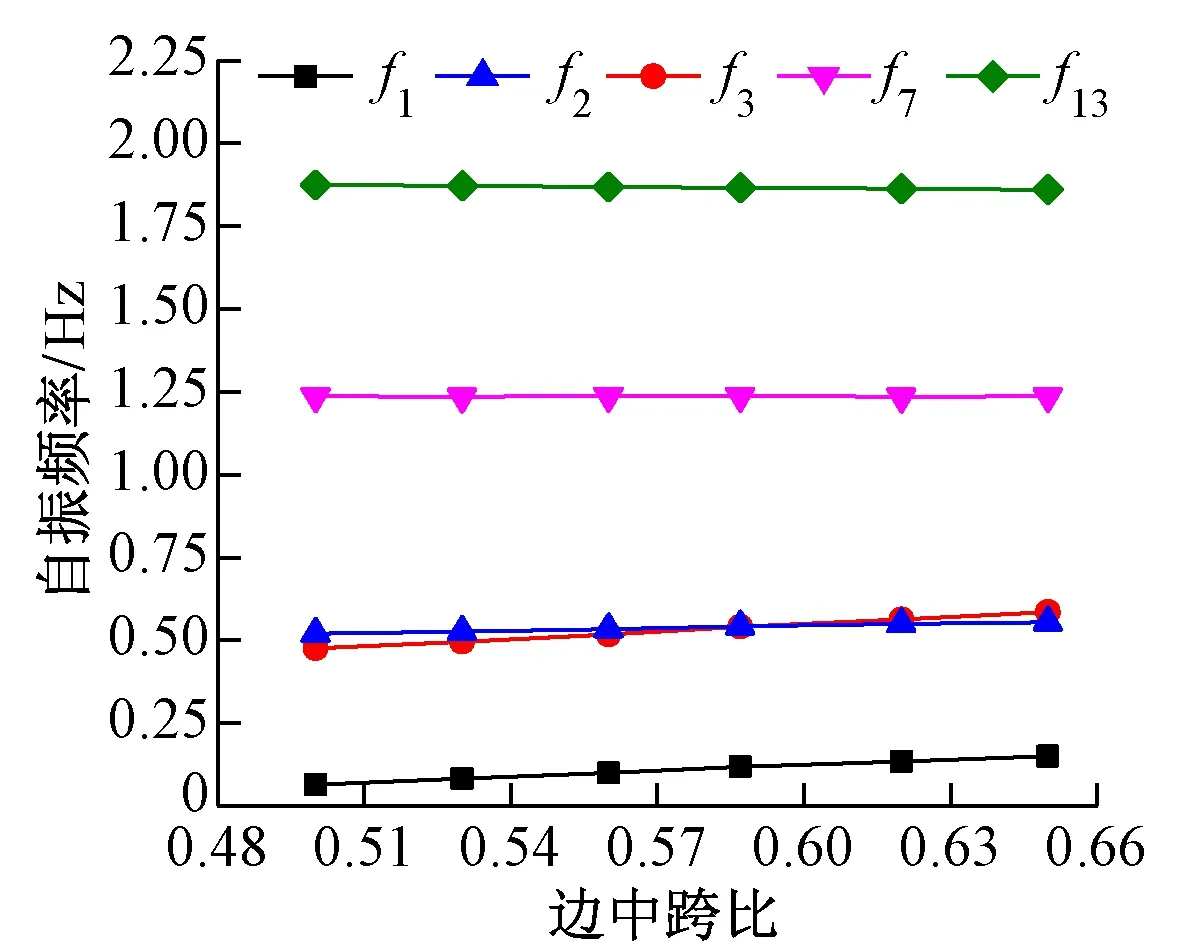
图4 边中跨比对自振频率的影响
合理的边中跨比可以有效调节独塔非对称混合梁斜拉桥的刚度分布,保证桥梁处于合理受力状态的同时,可以大幅提高其跨越能力[10]。在桥梁总长度不变的条件下,通过改变主塔的位置得到不同的边中跨比,研究其对桥梁动力特性的影响。结果见图4。可知,边中跨比由0.50变化至0.65时:①f1和f13几乎没有变化,说明边中跨比对主塔振型无影响;②f2和f3分别增加了23%和6%,原因是边中跨比增加时主梁刚度发生了重分布;③f1提高幅度达135%,充分体现了半漂浮体系斜拉桥的柔性特点。
4.3 横向抗风支座
横向抗风支座对自振频率的影响见表2。可知,支座的存在对主梁振型影响显著,对桥塔振型影响不大,表现在解除该支座后该桥总体频率下降,且第2阶振型由主梁竖弯变为主梁侧弯。原因是解除该支座后主梁的面外刚度降低,导致侧弯振型提前[11]。

表2 横向抗风支座对自振频率的影响
4.4 结构自重与刚度
本文研究主梁和桥塔自重、斜拉索和主梁刚度参数按照0.50,0.75,1.00,1.25,1.50,1.75,2.00的倍数变化时,大跨度铁路独塔混合梁斜拉桥自振频率的改变情况[12]。其中主梁自重和刚度按混凝土段和钢结构段同倍数改变[13]。
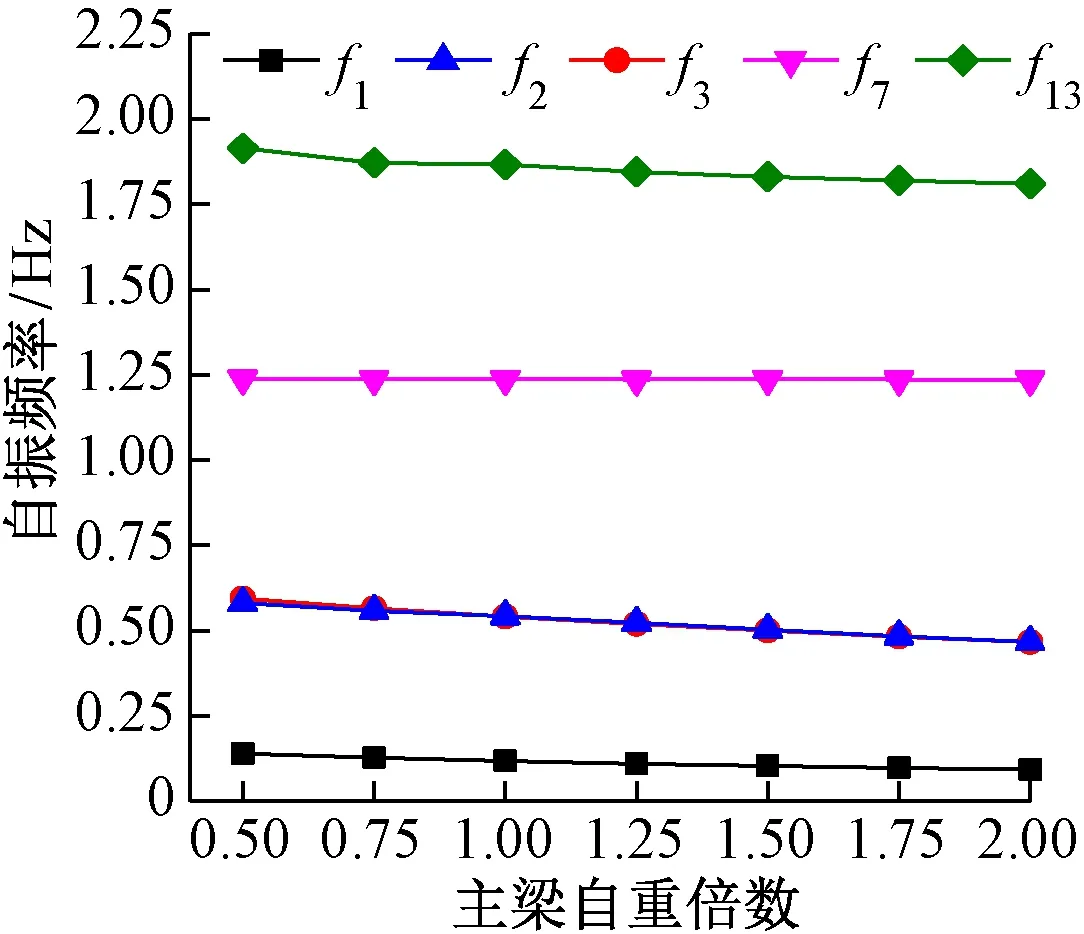
图5 主梁自重对自振频率的影响
主梁自重对自振频率的影响见图5。可知,主梁自重变化对f1,f2,f3的影响非常明显,当主梁自重倍数为2.00时,前3阶振型的自振频率分别下降了34%,22%和20%,但主塔的振型几乎无变化。原因是增加主梁的自重虽然能够改变其重力刚度,但也改变了平动刚度,且桥梁平动刚度的增大对动力特性的影响更加显著。因此大跨度铁路独塔混合梁斜拉桥在设计时应尽量选用轻质材料,从而减小自重对桥梁动力特性的影响。
桥塔自重对自振频率的影响见图6。可知,桥塔自重增加,桥梁各阶振型的自振频率均不同程度下降,f1,f2,,f3,f7,f13分别下降了11%,11%,32%,38%和37%。由此可见,桥塔自重的增加除了可以有效降低主塔侧弯和纵弯频率外,也会显著影响主梁竖弯和侧弯振型。

图6 桥塔自重对自振频率的影响
斜拉索刚度对自振频率的影响见图7。可知,f1,f3,f13对拉索的刚度变化最为敏感,随着斜拉索刚度的不断增加,其分别提高了10%,57%和46%,且主梁竖弯振型较侧弯振型提前。说明斜拉索刚度的增加使得桥梁的整体刚度增加,尤其对主梁和主塔面内刚度的影响较大,对主梁和主塔面外刚度影响甚微。
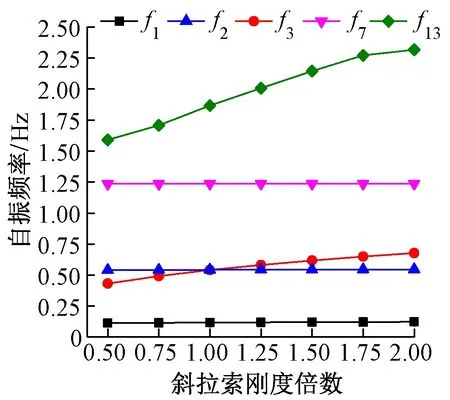
图7 斜拉索刚度对自振频率的影响

图8 主梁刚度对自振频率的影响
主梁刚度对自振频率的影响见图8。可知,主梁刚度的变化对f1,f7,f13几乎没有影响,但对f2和f3影响显著。随着主梁刚度的增加,f2从 0.501 Hz增加到0.582 Hz,增加了16%,f3从0.438 Hz增加到0.695 Hz,增加了59%。
4.5 辅助墩
在斜拉桥结构体系中,辅助墩可有效减小主跨主梁的弯矩和挠度,使桥梁受力更合理[14]。本文分析无主跨辅助墩、无边跨辅助墩和无边主跨辅助墩情况下桥梁的动力特性。其中,P1为边跨边墩,P2,P3为边跨辅助墩,P5为主跨辅助墩,P6为主跨边墩(参见图1)。辅助墩对自振频率的影响见表3。可知:①辅助墩的存在会显著提高桥梁结构的整体刚度,使结构自振频率增大,尤其对桥梁基频提高幅度最大;②无辅助墩时,桥梁结构的各阶振型中的第1阶振型由纵飘变为了边墩或辅助墩纵弯;③边跨辅助墩对结构振型的振动频率的影响比主跨辅助墩对结构振型的振动频率的影响要大;④无辅助墩时,主梁侧弯和竖弯发生顺序整体推后。

表3 辅助墩对自振频率的影响
5 结论
1)岳口汉江特大桥主要振型依次为纵飘、主梁一阶竖弯、主梁一阶侧弯,振型排列合理,不易出现耦合振动。
2)主梁钢混比和边中跨比的变化可极大地改变纵飘振型的振动频率,但对主塔面内和面外振型影响甚微;横向抗风支座的有无对主梁振型影响较大,但对桥塔振型影响不大,无抗风支座时桥梁频率下降。
3)辅助墩的存在会显著提高桥梁结构的整体频率,尤其对基频提高幅度最大;无辅助墩时桥梁结构的各阶振型出现了重组现象,一阶振型由纵飘变为了边墩或辅助墩纵弯。
4)主梁自重主要影响了该桥前3阶振型的振动频率;桥塔自重提高时,桥梁各阶振型的振动频率均出现不同程度的下降;主梁刚度对该桥主梁侧弯和竖弯振型影响较大;斜拉索刚度对主塔纵弯和主梁竖弯振型影响显著。
5)设计大跨度铁路独塔混合梁斜拉桥时,应优化钢混比、边中跨比、辅助墩位置、结构自重和刚度等参数,以提高结构的抗风抗震能力,获得最优的动力特性。
